Backtracking¶
Question¶
What is the output of below code for N = 7 ?
int magicfun( int N) {
if ( N == 0)
return 0;
else
return magicfun(N/2) * 10 + (N % 2);
}
Choices
- 100
- 111
- 99
- 112
Explanation
magicfun(7)
magicfun(3) * 10 + 1
magicfun(1) * 10 + 1
magicfun(0) * 10 + 1
0
Question¶
Time complexity of below code is?
int magicfun( int N) {
if ( N == 0)
return 0;
else
return magicfun(N/2) * 10 + (N % 2);
}
Choices
- O(log N)
- O(1)
- O(N)
- O(N/2)
Everytime we are dividing N by 2. Hence complexity will be log N.
Question¶
Output of below code is?
void fun(char s[], int x) {
print(s)
char temp
if(x < s.length/2) {
temp=s[x]
s[x] = s[s.length-x-1]
s[s.length-x-1]=temp
fun(s, x+1)
}
}
Run for fun("SCROLL", 0)
Choices
- SCROLL
SCROLL
SCROLL
SCROLL - SCROLL
LCROLS
LLROCS
LLORCS - LLORCS
SCROLL
LCROLS
LLROCS
We start with
(SCROLL, 0); line 2 runs; print => SCROLL
since 0 < 6/2, we run the if block and index 0 gets swapped with 5
(LCROLS, 1); line 2 runs; print => LCROLS
since 1 < 6/2, we run the if block and index 1 gets swapped with 4
(LLROCS, 2); line 2 runs; print => LLROCS
since 2 < 6/2, we run the if block and index 2 gets swapped with 3
(LLORCS, 3); line 2 runs; print => LLORCS
since 3 not less than 6/2, we skip if block and come back from recursion
Question¶
Time Complexity of below code is?
void fun(char s[], int x) {
print(s)
char temp
if(x < s.length/2) {
temp=s[x]
s[x] = s[s.length-x-1]
s[s.length-x-1]=temp
fun(s, x+1)
}
}
Choices
- O(N2)
- O(1)
- O(N)
- O(N/2)
We are only iterating till half of the string. In the worst case, we can start at 0th index.
Therefore, #iterations = N/2
Hence, T.C = O(N)
S.C is also O(N) since call will be made for half of the string.
What is Backtracking¶
The above process is known as Backtracking.
Let's try to understand the concept of backtracking by a very basic example. We are given a set of words represented in the form of a tree. The tree is formed such that every branch ends in a word.
![]()
Our task is to find out if a given word is present in the tree. Let's say we have to search for the word AIM. A very brute way would be to go down all the paths, find out the word corresponding to a branch and compare it with what you are searching for. You will keep doing this unless you have found out the word you were looking for.
![]()
In the diagram above our brute approach made us go down the path for ANT and AND before it finally found the right branch for the word AIM.
The backtracking way of solving this problem would stop going down a path when the path doesn't seem right. When we say the path doesn't seem right we mean we come across a node which will never lead to the right result. As we come across such node we back-track. That is go back to the previous node and take the next step.
![]()
In the above diagram backtracking didn't make us go down the path from node N. This is because there is a mismatch we found early on and we decided to go back to the next step instead. Backtracking reduced the number of steps taken to reach the final result. This is known as pruning the recursion tree because we don't take unnecessary paths.
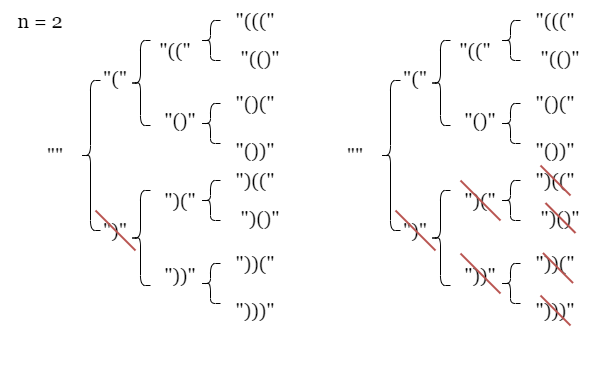
Problem 1 : Print Valid Parenthesis Continued¶
Explanation¶
As shown in the picture below:
) is an invalid string, so every string prefixed with it is also invalid, and we can just drop it.
To ensure that the current string is always valid during the backtracking process, we need two variables left_count and right_count that record the number of left and right parentheses in it, respectively.
Therefore, we can define our recursive function as solve(cur_string, left_count, right_count) that takes the current string, the number of left parentheses, and the number of right parentheses as arguments. This function will build valid combinations of parentheses of length 2n recursively.
The function adds more parentheses to cur_string only when certain conditions are met:
-
If
left_count < n, it suggests that a left parenthesis can still be added, so we add one left parenthesis to cur_string, creating a new string new_string = cur_string + (, and then callsolve(new_string, left_count + 1, right_count). -
If
left_count > right_count, it suggests that a right parenthesis can be added to match a previous unmatched left parenthesis, so we add one right parenthesis to cur_string, creating a new string new_string = cur_string + ), and then call solve(new_string, left_count, right_count + 1).
This function ensures that the generated string of length 2n is valid, and adds it directly to the answer. By only generating valid strings, we can avoid wasting time checking invalid strings.
Dry Run for N = 2, means overall length will be 4.¶
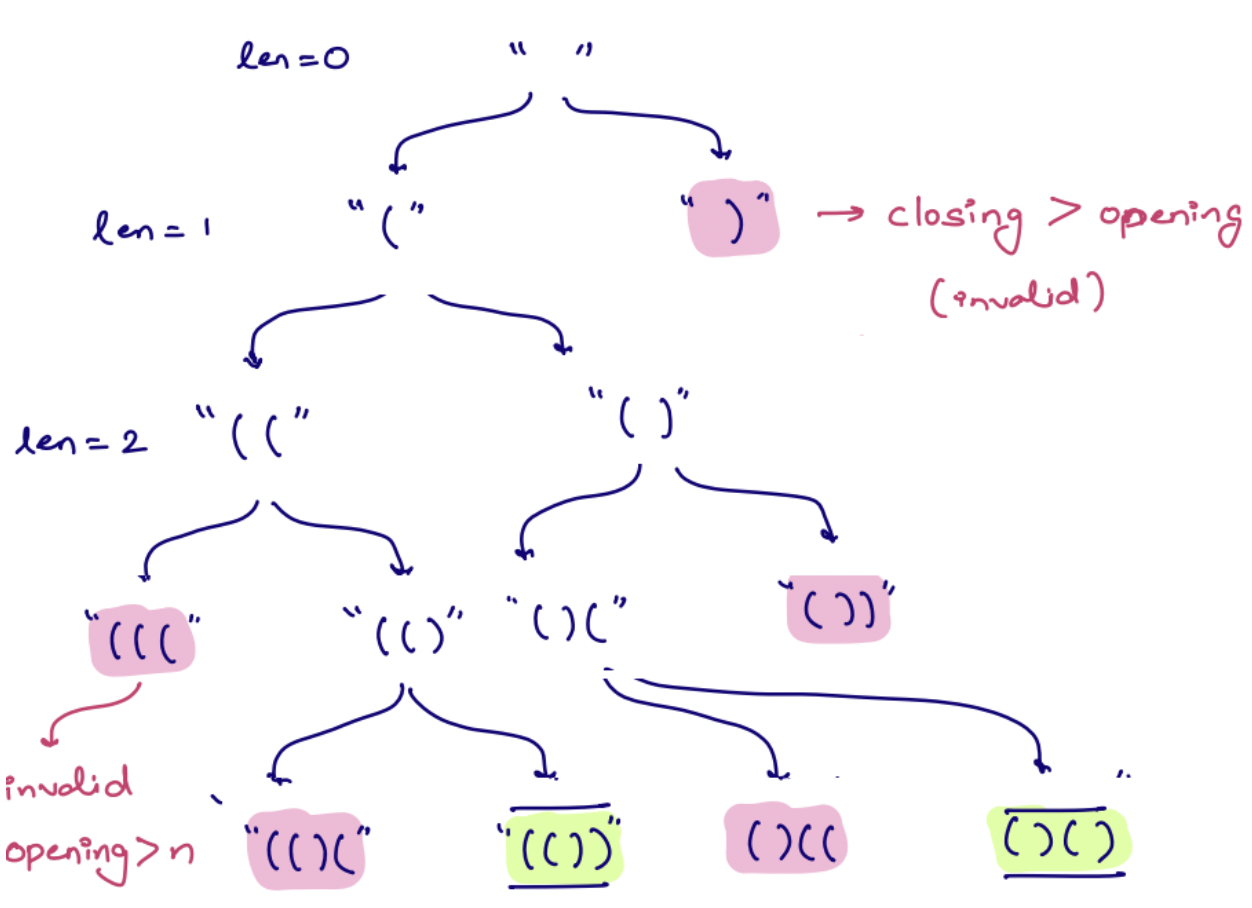
- Here "(())" and "()()" are valid answers.
PseudoCode¶
void solve(str, N, opening, closing) { //also taking given N value in parameter
// base case
if (str.length() == 2 N) {
print(str);
return;
}
if (opening < N) {
solve(N, str + '(', opening + 1, closing)
}
if (closing < opening) {
solve(N, str + ')', opening, closing + 1)
}
}
Complexity¶
- Time Complexity: O(2N )
- Space Complexity: O(N)
Definition of Subset and Subsequences¶
Definition of Subset and Example¶
A subset is often confused with subarray and subsequence but a subset is nothing but any possible combination of the original array (or a set).
For example, the subsets of array arr = [1, 2, 3, 4, 5] can be:
[3, 1]
[2, 5]
[1, 2], etc.
So, we can conclude that subset is the superset of subarrays i.e. all the subarrays are subsets but vice versa is not true.
Definition of Subsequence and Example¶
As the name suggests, a subsequence is a sequence of the elements of the array obtained by deleting some elements of the array. One important thing related to the subsequence is that even after deleting some elements, the sequence of the array elements is not changed. Both the string and arrays can have subsequences.
The subsequence should not be confused with the subarray or substring. The subarray or substring is contiguous but a subsequence need not to be contiguous.
For example, the subsequences of the array arr : [1, 2, 3, 4] can be:
[1, 3]
[2, 3, 4]
[1, 2, 3, 4], etc.
Note: A subarray is a subsequence, a subsequence is a subset but the reverse order is not correct.
Problem 2 Subsets¶
Given an array with distinct integers. Print all the subsets using recursion.
Example
Input: [1, 2, 3]
Output: {[], [1], [2], [3], [1, 2], [1, 3], [2, 3], [1, 2, 3]}
Total Subsets possible are 2N
For every element, there can be two options:
- It is considered as part of a subset
- It is not considered as part of a subset
Say there are 3 elements, for each of them we have above two options, hence 2 * 2 * 2 = 2N are the total options.
Warning
Please take some time to think about the solution approach on your own before reading further.....
Approach¶
The approach to solve the problem is to use backtracking.
For each element, I have two choices whether to keep it or not, I execute my choice and then ask recursion to do the remaining work.
Let us take an example of [1, 2, 3].

Psuedocode¶
list < list < int >> ans;
void subsets(list < int > A, list < int > currset, int idx) {
//base case
if (idx == A.size()) {
ans.add(currset);
return;
}
//for every ele in A, we have 2 choices
//choice 1 : keep it in currset
currset.add(A[idx]);
subsets(A, currset, idx + 1);
//choice 2 : Don't keep it in currset
currset.remove_back();
subsets(A, currset, idx + 1);
}
NOTE: For producing individual sorted subsets, we need to sort the given array first. We will get the desired result with this since elements are being processed in sequence.
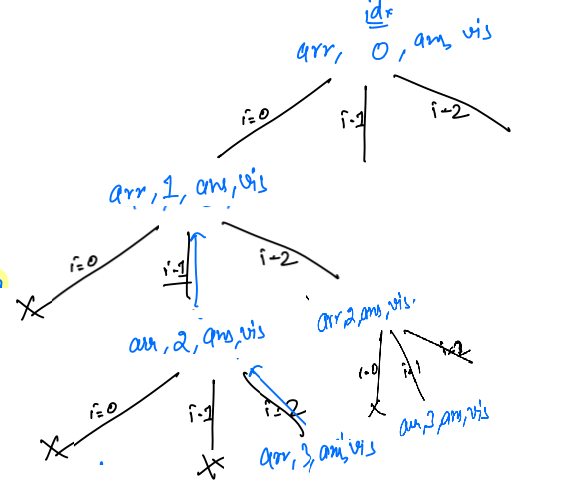
Dry Run¶
A = {2, 6, 9}
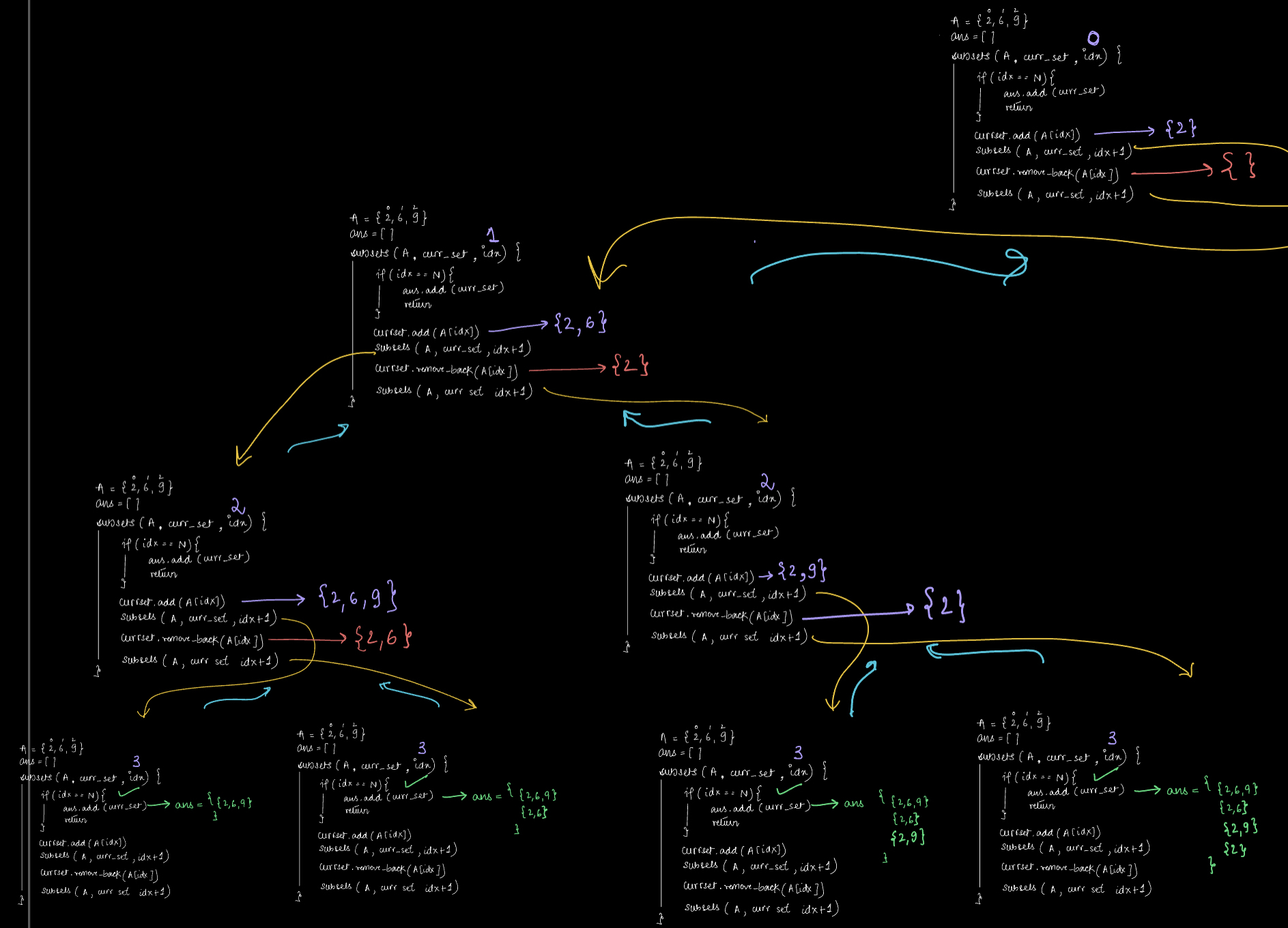
Continued
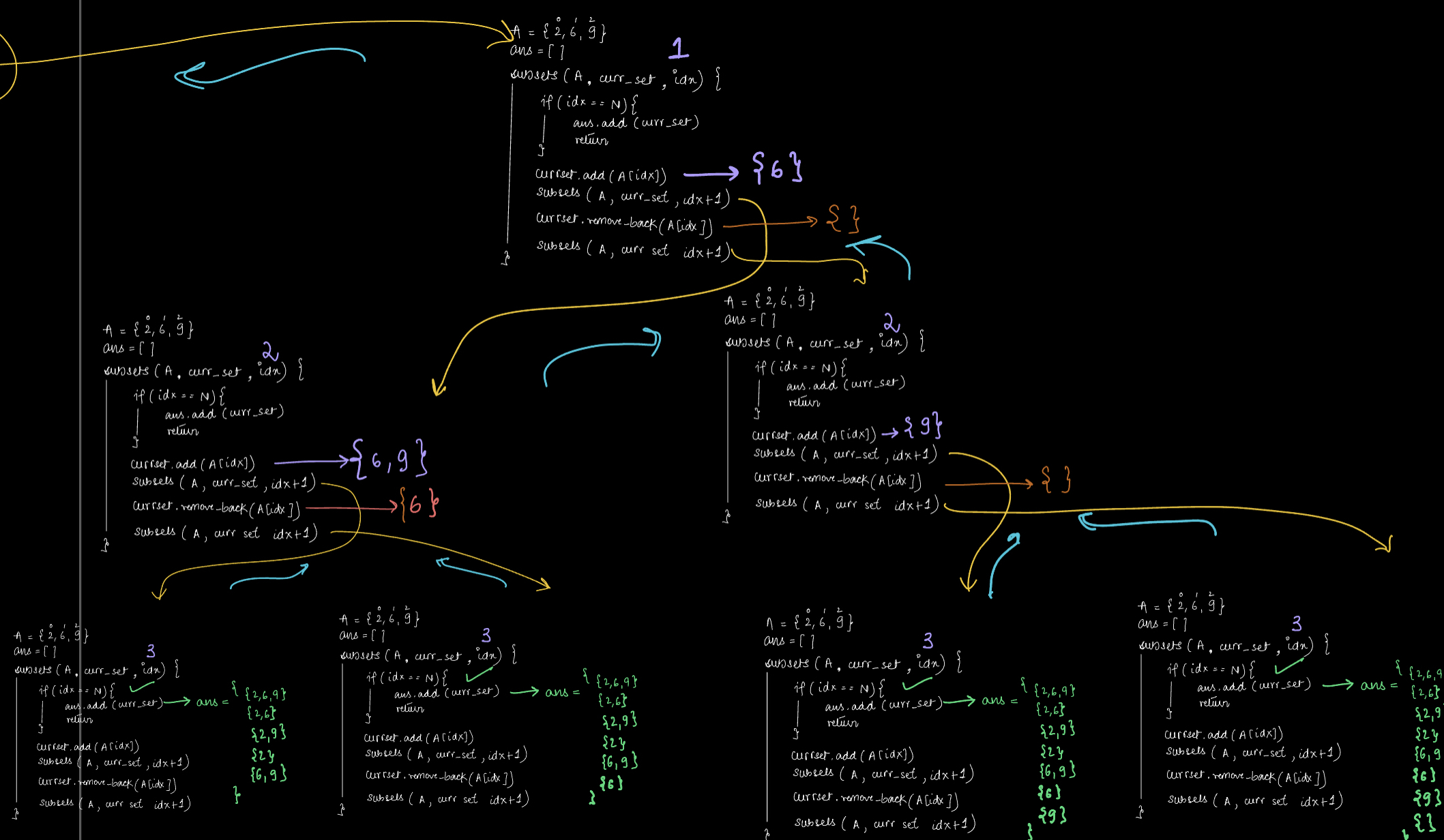
Complexity¶
- Time Complexity: O(2N)
- Space Complexity: O(N)
Question¶
What is the count of total permutations of a string with unique characters? (N=String length)
Choices
- N2
- N + (N + 1) / 2
- N * (N - 1) / 2
- N!
Problem 3 : Permutation¶
Given a character array with distinct elements. Print all permutations of it without modifying it.
Example For string abc, of length 3, we have total 3! = 6 permutations:
- abc
- acb
- bac
- bca
- cab
- cba
Input: abc
Output: abc acb bac bca cab cba
Constraint
We don't have duplicate characters in a string.
Permutations Idea¶
- Every permutation has n number of characters, where n is the length of the original string.
- So initially we have n number of empty spots.
_ _ _ - And we need to fill these empty spots one by one.
- Let us start with the first empty spot, which means from the 0th index.
- For the 0th index we have three options,
a, b, and c, any of the three characters can occupy this position.
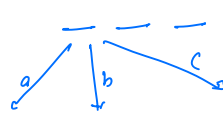
- If
awill occupy 0th index, then we havea _ _, and ifbwill occupy 0th index, then we haveb _ _, and ifcwill occupy 0th index, then we havec _ _,
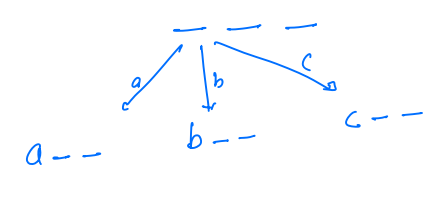
- Now the first spot is occupied, now we have to think about the second spot.
- Now for a second spot we have only options left.
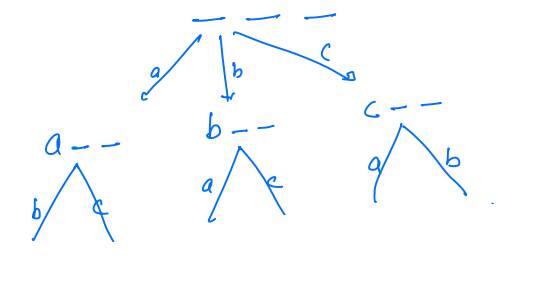
- Now when the character occupies the second spot, then we get.
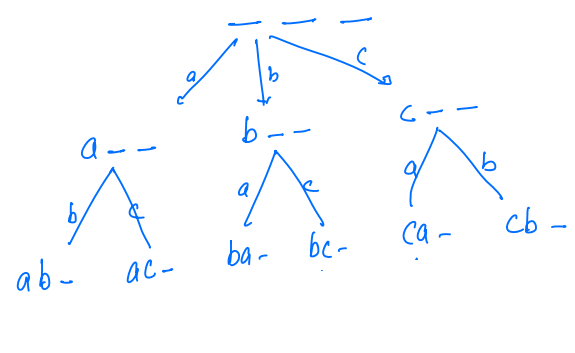
- Now for the last spot, every string has left with a single character, like in
a b _, we are only left with the characterc.
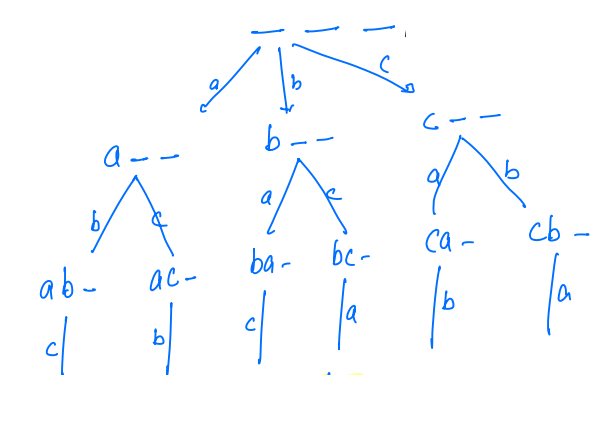
- Now this character will occupy the last spot.
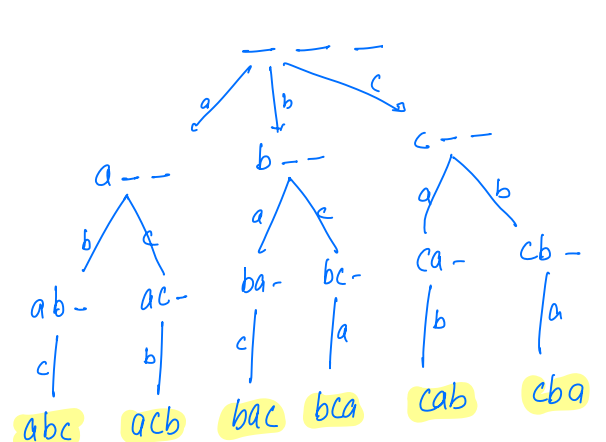
We are setting characters at positions one by one. So We need to keep track of visited/used characters.
Permutations PsuedoCode¶
void permutations1(char[] arr, idx, ans[N], visited[N]) {
if (idx == arr.length) {
print(ans[])
return
}
for (i = 0; i < N; i++) { // All possibilities
if (visited[i] == false) { // valid possibilities
visited[i] = true;
ans[idx] = arr[i];
permutations1(arr, idx + 1, ans, visited); // recursive call for next index
visited[i] = false; //undo changes
}
}
}
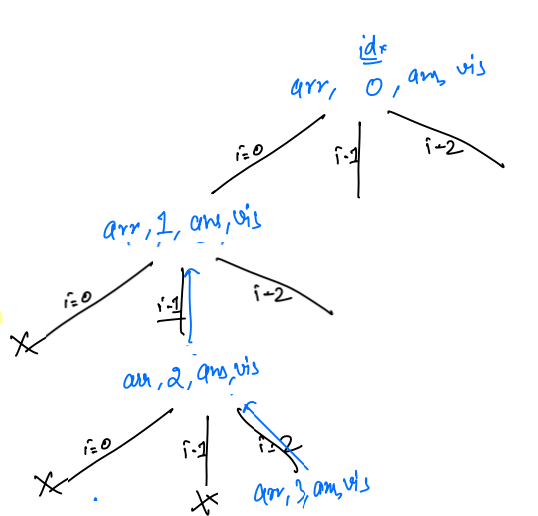
Permutations - Dry Run¶
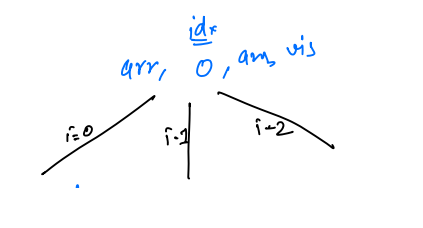
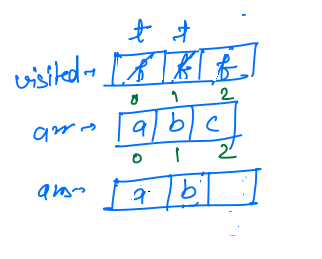
Let us suppose we have the string arr[] = a b c , and initially ans array is empty, ans[] = _ _ _.
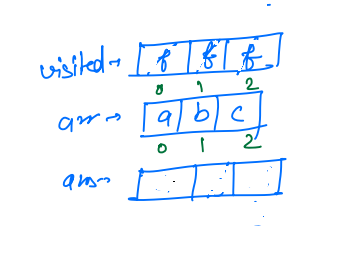
- Initially, we are at index 0,
- Now i vary from 0 to
n-1, so it will go from 0 to 2, as here the length of the string is 3.
- Now when
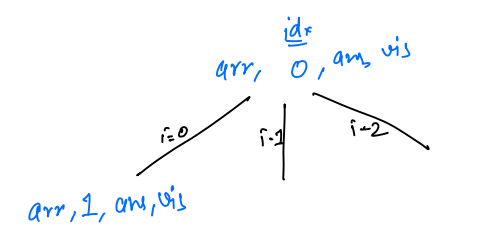
i = 0, we will check thatvisited[i] == false, so this condition is true, we markvisited[i] == trueandans[0] = arr[0] = a.
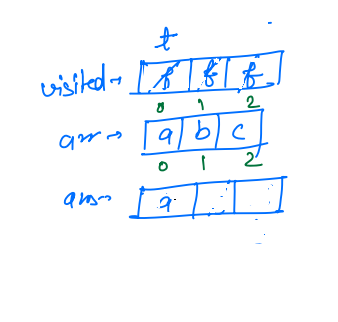
- Now it makes a recursive call for the next index,
permutations1(arr, 1, ans, visited)
- Inside this call,
idx != arr.length, so we will continue further, now inside this call, the loop will go from 0 to 2.
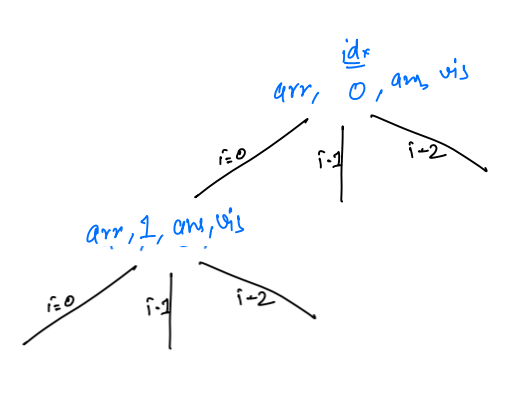
-
But in case
i = 0, nowvisited[0] != false, so in this iteration we will not enter inside the if condition, i will simply get incremented. -
Now
i = 1, we will check thatvisited[i] == false, so this condition is true, we markvisited[1] == trueandans[1] = arr[1] = b.
- Now it will make recussive call for
idx + 1,permutations1(arr, 2, ans, visited)
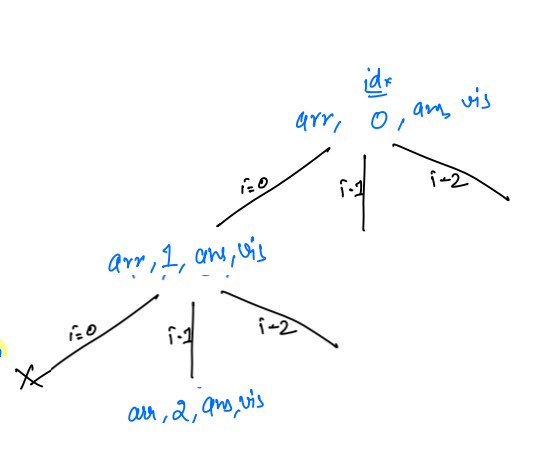
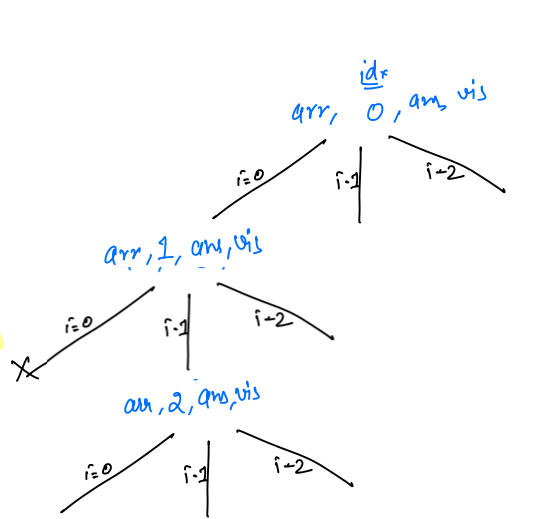
- Now inside this new recursive again loop will run from 0 to 2.
- Now when
i = 0, nowvisited[0] != false, so in this iteration, we will not enter inside the if condition, i will simply get incremented. - Now
i = 1, againvisited[1] != false, so in this iteration, we will not enter inside the if condition, i will simply get incremented.
- Now
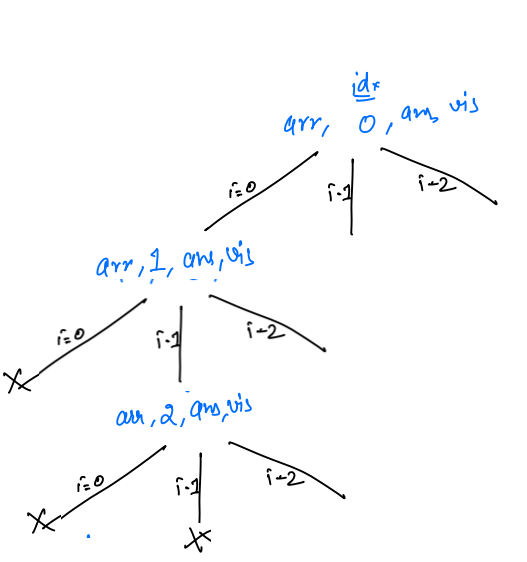
i = 2, we will check thatvisited[i] == false, so this condition is true, we markvisited[2] == trueandans[2] = arr[2] = c.
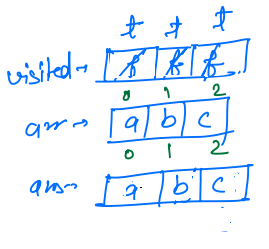
- Now it will make recussive call for
idx + 1,permutations1(arr, 3, ans, visited)
- Inside this call, our
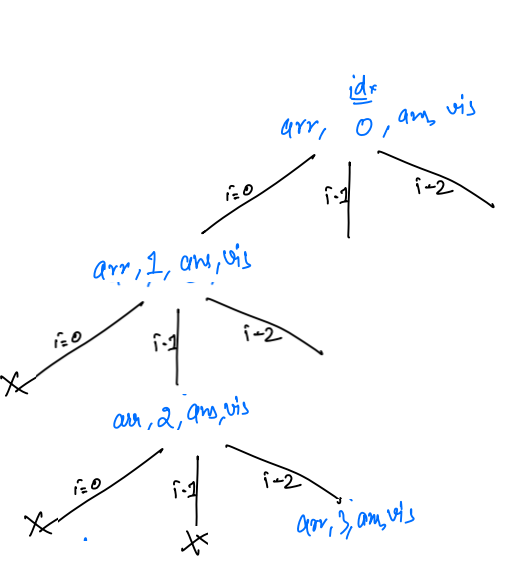
idx == arr.length, so printans, so abc will be printed, and it will return. And after returningvisited[2] = false.
- Now for
arr, 2, ans, visited, all iterations are completed. So it will also return andvisited[1] = false
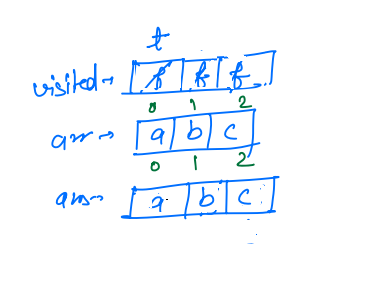
- Now for
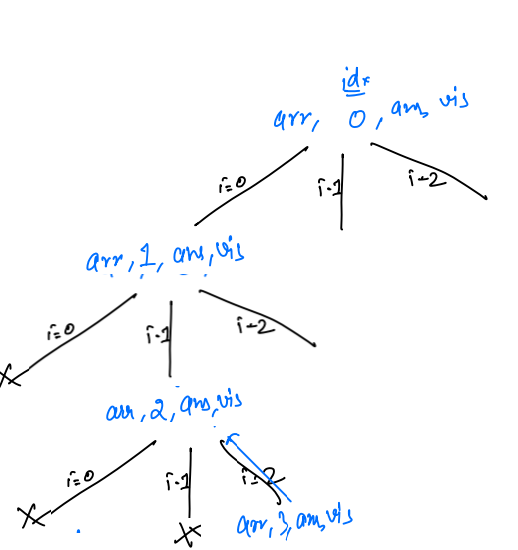
arr, 1, ans, visited, we are left for the iterationi = 2, so it will check forvisited[i] == false, asvisited[2] = false, so go inside the if condition andvisited[2] == trueandans[1] = arr[2] = c
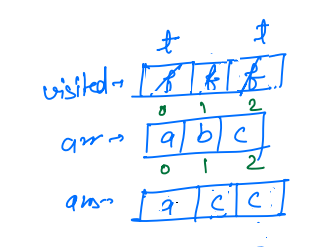
- Now it will make the recursive call for
arr, 2, ans, visited. And inside this call again loop will run from 0 to 2. Nowvisited[0] == true, so it will fori = 1, and so it will check forvisited[i] == false, asvisited[1] = false, so go inside the if condition andvisited[1] == trueandans[2] = arr[1] = b
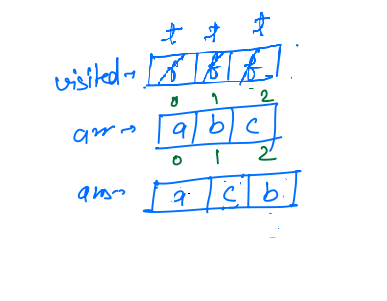
- Now it will make recussive call for
idx + 1,permutations1(arr, 3, ans, visited)
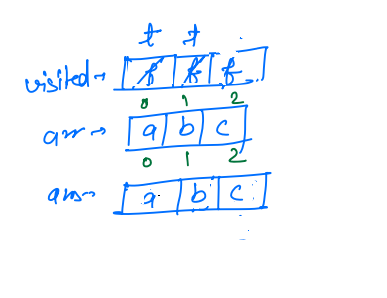
- Now inside this call
idx == arr.length, so it will printans, so acb will be printed, and it will return.
In this way, all the permutations will be printed.
