Bit Manipulation 1¶

Truth Table for Bitwise Operators¶

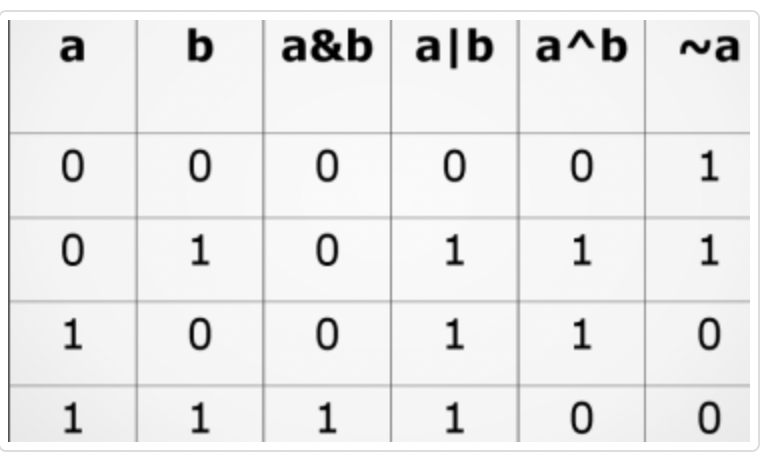
Below is the truth table for bitwise operators.

Basic AND XOR OR Properties¶

Basic AND Properties¶

Even/Odd Number In binary representation, if a number is even, then its least significant bit (LSB) is 0. Conversely, if a number is odd, then its LSB is 1.

A & 1 = 1 (if A is odd)

181 = 10110101 //181 is odd, therefore LSB is 1

10110101 & 1 = 1 // Performing Bitwise AND Operation

Since, 181 is odd, Bitwise AND with 1 gave 1.

A & 1 = 0 (if A is even)

180 = 10110100 //180 is even, therefore LSB is 0

10110100 & 1 = 0 // Performing Bitwise AND Operation

Since, 180 is even, Bitwise AND with 1 gave 0.

A & 0 = 0 (for all values of A)
A & A = A (for all values of A)

Basic OR Properties¶

A | 0 = A (for all values of A)
A | A = A (for all values of A)

Basic XOR Properties¶

A ^ 0 = A (for all values of A)
A ^ A = 0 (for all values of A)

Commutative Property¶

The order of the operands does not affect the result of a bitwise operation.

A & B = B & A // Bitwise AND
A | B = B | A // Bitwise OR
A ^ B = B ^ A // Bitwise XOR

Associative Property¶

It states that the grouping of operands does not affect the result of the operation.
In other words, if we have three or more operands that we want to combine using a bitwise operation, we can group them in any way we want, and the final result will be the same.

(A & B) & C = A & (B & C) // Bitwise AND
(A | B) | C = A | (B | C) // Bitwise OR
(A ^ B) ^ C = A ^ (B ^ C) // Bitwise XOR

Question¶

Evaluate the expression: a ^ b ^ a ^ d ^ b

Choices

a ^ b ^ a ^ b
b
b ^ d
d

We can evaluate the expression as follows:

a ^ b ^ a ^ d ^ b = (a ^ a) ^ (b ^ b) ^ d // grouping the a's and the b's
= 0 ^ 0 ^ d // since a ^ a and b ^ b are both 0
= d // the result is d

Therefore, the expression a ^ b ^ a ^ d ^ b simplifies to d.

Question¶

Evaluate the expression: 1 ^ 3 ^ 5 ^ 3 ^ 2 ^ 1 ^ 5

Choices

5
3
2
1

We can evaluate the expression as follows:

1 ^ 3 ^ 5 ^ 3 ^ 2 ^ 1 ^ 5 = ((1 ^ 1) ^ (3 ^ 3) ^ (5 ^ 5)) ^ 2 // grouping the pairs of equal values and XORing them
= (0 ^ 0 ^ 0) ^ 2 // since x ^ x is always 0
= 0 ^ 2 // since 0 ^ y is always y
= 2 // the result is 2

Therefore, the expression 1 ^ 3 ^ 5 ^ 3 ^ 2 ^ 1 ^ 5 simplifies to 2.

Left Shift Operator (<<)¶

The left shift operator (<<) shifts the bits of a number to the left by a specified number of positions.
The left shift operator can be used to multiply a number by 2 raised to the power of the specified number of positions.

Example: a = 10
Let's see a dry run on smaller bit representation(say 8)
Binary Representation of 10 in 8 bits: 00001010

(a << 0) = 00001010 = 10
(a << 1) = 00010100 = 20  (mutiplied by 2)
(a << 2) = 00101000 = 40  (mutiplied by 2)
(a << 3) = 01010000 = 80  (mutiplied by 2)
(a << 4) = 10100000 = 160 (mutiplied by 2)
(a << 5) = 01000000 = 64  (overflow, significant bit is lost)

In general, it can be formulated as:

a << n = a * 2^n
1 << n = 2^n

However, it's important to note that left shifting a number beyond the bit capacity of its data type can cause an overflow condition.

In above case, if we shift the number 10 more than 4 positions to the left an overflow will occur.

(a << 5) = 01000000 = 64 
//(incorrect ans due to overflow)
// correct was 320 but it is too large to get stored in 8 bits

Note: We can increase the number of bits, but after a certain point it will reach limit and overflow will occur.

Right Shift Operator (>>)¶

The right shift operator (>>) shifts the bits of a number to the right by a specified number of positions.
When we right shift a binary number, the most significant bit (the leftmost bit) is filled with 0.
Right shift operator can also be used for division by powers of 2.

Let’s take the example of the number 20, which is represented in binary as 00010100. Lets suppose, it can be represented just by 8 bits.

(a >> 0) = 00010100 = 20
(a >> 1) = 00001010 = 10 (divided by 2)
(a >> 2) = 00000101 = 5  (divided by 2)
(a >> 3) = 00000010 = 2  (divided by 2)
(a >> 4) = 00000001 = 1  (divided by 2)
(a >> 5) = 00000000 = 0  (divided by 2)

In general, it can be formulated as:

a >> n = a/2^n
1 >> n = 1/2^n

Here, overflow condition doesn't arise.

Question¶

What will we get if we do 1 << 3 ?

Choices

1
8
3
4

Power of Left Shift Operator¶

OR( | ) Operator¶

Left Shift Operator can be used with the OR operator to SET the i^th bit in the number.

N = (N | (1<<i))

It will SET the i^th bit if it is UNSET else there is no change.

Example

XOR( ^ ) Operator¶

Left Shift Operator can be used with the XOR operator to FLIP(or TOGGLE) the i^th bit in the number.

N = (N ^ (1<<i))

After applying the operation, if the i^th bit is SET, then it will be UNSET or vice-versa.

Example

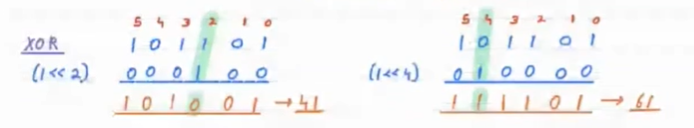
AND( & ) Operator¶

Left Shift Operator can be used with AND operator to check whether the i^th bit is set or not in the number.

X = (N & (1<<i))

if the value of X is 0 then the i^th bit is unset. Else the i-th bit is set.

Example

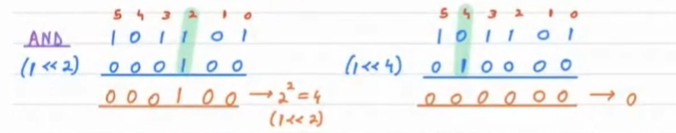
Problem 1 Check whether ith bit in N is SET or not¶

Check whether the i^th bit in N is SET or not.

Approach¶

Taking AND with 1 can help us.
0 & 1 = 0
1 & 1 = 1

We can shift 1 to the ith bit.
If X = (N & (1<<i))
- if X > 0, then i^th bit is set.
- else i^th bit is not set.

Example

Suppose we have

N = 45
i = 2

The binary representation of 45 is:

1 0 1 1 0 1

The binary representation of (1<<2) is:

0 0 0 1 0 0

45 & (1<<2) is

0 0 0 1 0 0

It is greater than 0. Hence i^th bit is SET.

Pseudocode¶

function checkbit(int N, int i) {
    if (N & (1 << i)) {
        return true;
    } else {
        return false;
    }
}

Complexity¶

Time Complexity - O(1).
Space Complexity - O(1).

Problem 2 Count the total number of SET bits in N¶

Given an integer N, count the total number of SET bits in N.

Input

N = 12

Output

Warning

Please take some time to think about the solution approach on your own before reading further.....

Approach 1¶

Iterate over all the bits of integer(which is maximum 32) and check whether that bit is set or not. If it is set then increment the answer(initially 0).

function countbit(int N) {
    int ans = 0;
    for (i = 0; i < 32; i++) {
        if (checkbit(N, i)) {
            ans = ans + 1;
        }
    }
    return ans;
}

Here, checkbit function is used to check whether the i^th bit is set or not.

Approach 2¶

To count the number of SET bits in a number, we can use a Right Shift operator as:

Initialize a count variable to zero.
While the number is not equal to zero, do the following:
- Increment the count variable if the 0^th bit of the number is 1.
- Shift the number one bit to the right.
- Repeat steps a and b until the number becomes zero.
Return the count variable.

function countbit(int N) {
    int ans = 0;
    while (N > 0) {
        if (N & 1) {
            ans = ans + 1;
        }
        N = (N >> 1);
    }
    return ans;
}

Question¶

What is the time complexity to count the set bits ?

Choices

log N
N
N^2
1

Explanation

For both of the above approaches,

Time Complexity - O(log₂(N))

Since N is being repeatedly divided by 2 till it is > 0.

Space Complexity - O(1).

Problem 3 Unset the ith bit of the number N if it is set¶

UNSET the i^th bit of the number N if it is set.

Example

Suppose we have a number N = 6
Binary Representation of 6:

1 1 0 0

We have to unset its 2^nd bit

1 0 0 0

Approach¶

First of all, we can check if the bit is set or not by taking & with 1.

X = (N & (1<<i))

Then, we have two condition:

if X > 0, it means the i^th bit is SET. To UNSET that bit do: N = (N ^ (1<<i)) {XOR with 1 toggles the bit}
else if it is UNSET, no need to do anything.

Pseudocode¶

Function unsetbit(int N, int i) {
    int X = (N & (1 << i));
    if (checkbit(N, i)) {
        N = (N ^ (1 << i));
    }
}

Complexity¶

Time Complexity - O(1)
Space Complexity - O(1)

Problem 4 SET bits in a range¶

A group of computer scientists is working on a project that involves encoding binary numbers. They need to create a binary number with a specific pattern for their project. The pattern requires A 0's followed by B 1's followed by C 0's. To simplify the process, they need a function that takes A, B, and C as inputs and returns the decimal value of the resulting binary number. Can you help them by writing a function that can solve this problem efficiently?

Constraints:

0 <= A, B, C <= 20

Example:

A = 4
B = 3
C = 2

Output:

Explanation:

The corresnponding binary number is "000011100" whose decimal value is 28.

Solution Explanation:¶

We can take a number 0 and set the bits from C to B+C-1 (0 based indexing from right)

Say initially we have -

8	7	6	5	4	3	2	1	0
0	0	0	0	0	0	0	0	0

A = 4
B = 3
C = 2

It means, we will set the bits from 2( C) to 4(B+C-1) from right

This is how the number will look like finally -

8	7	6	5	4	3	2	1	0
0	0	0	0	1	1	1	0	0

How to set a bit ?

We can take OR(|) with (1<<i)

Pseudocode¶

long solve(int A, int B, int C) {
    long ans = 0;
    for (int i = C; i < B + C; i++) {
        ans = ans | (1 << i);
    }
    return ans;
}

Please NOTE:

We have taken ans as long because A+B+C can go uptil total 60 bits as per constraints which can be stored in long but not in integers.