Bit Manipulation 2¶

Problem 1 Single Number 1¶

We are given an integer array where every number occurs twice except for one number which occurs just once. Find that number.

Example 1:

Input:

[4, 5, 5, 4, 1, 6, 6]

Output:

1 only 1 occurs single time

Example 2:

Input:

[7, 5, 5, 1, 7, 6, 1, 6, 4]

Output:

4 only 4 occurs single time

Warning

Please take some time to think about the solution approach on your own before reading further.....

Brute Force¶

Traverse the array and count frequency of every element one by one.

Time Complexity - O(N^2)
Space Complexity - O(1)

Using HashMap¶

Traverse the array and store frequency of every element.

Time Complexity - O(N)
Space Complexity - O(N)

Idea¶

What is A^A ?
ans = A^A is 0

Question¶

Value of 120 ^ 5 ^ 6 ^ 6 ^ 120 ^ 5 is -

Choices

Approach 1:¶

Since ^ helps to cancel out same pairs, we can use it.
Take XOR of all the elements.

Pseudocode¶

int x = 0;

for (int i = 0; i < arr.size(); ++i) {
    x = x ^ arr[i]; // XOR operation
}

print(x);

Complexity¶

Time Complexity: O(N)
Space Complexity: O(1)

Approach 2:¶

Interesting Solution!

Bitwise operators work on bit level, so let's see how XOR was working on bits. For that, let's write binary representation of every number.

Observations:¶

For every bit position, if we count the number of 1s the count should be even because numbers appear in pairs, but it can be odd if the bit in a single number is set for that position.

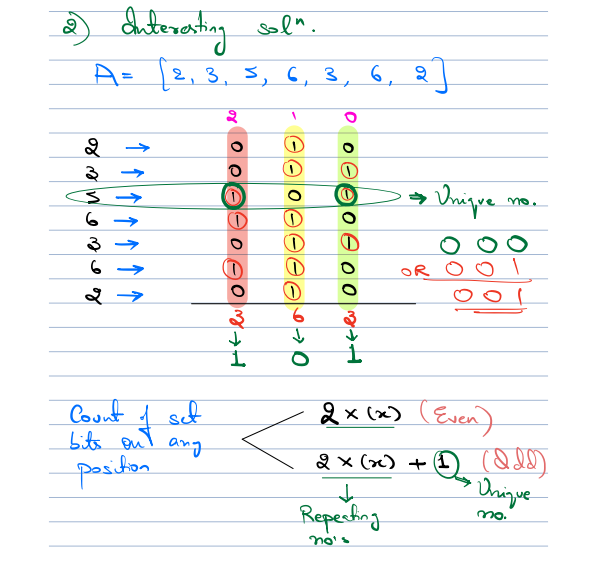
We will iterate on all the bits one by one.
We will count the numbers in the array for which the particular bit is set
If the count is odd, in the required number that bit is set.

Pseudocode¶

int ans = 0;

for (int i = 0; i < 32; i++) { // go to every bit one by one  
    int cnt = 0;

    for (int j = 0; j < arr.size(); j++) { // iterate on array

        // check if ith bit is set
        if ((arr[j] & (1 << i)) cnt++;
        }

        if (cnt & 1) // If the count is odd
            ans = ans | 1 << i; // set ith bit in ans
    }

    print(ans);

Complexity¶

Time Complexity: O(N)
Space Complexity: O(1)

Problem 2 Single number 2¶

Given an integer array, all the elements will occur thrice but one. Find the unique element.

Example

Input:

[4, 5, 5, 4, 1, 6, 6, 4, 5, 6]

Output:

1 Only 1 occurs a single time

Approach 1: Brute Force¶

Using two for loops and counting the occurence of each number.

Complexity¶

Time Complexity: O(N^2)
Space Complexity: O(1)

Approach 2: Hashmaps¶

Iterate on array and store frequency of each number in Hashmap. Iterate on array/map and return the number with frequency 1.

Complexity¶

Time Complexity: O(N)
Space Complexity: O(N)

Warning

Please take some time to think about the optimsed approach on your own before reading further.....

Approach 3: Best Approach¶

Hint can be taken from the previous question.

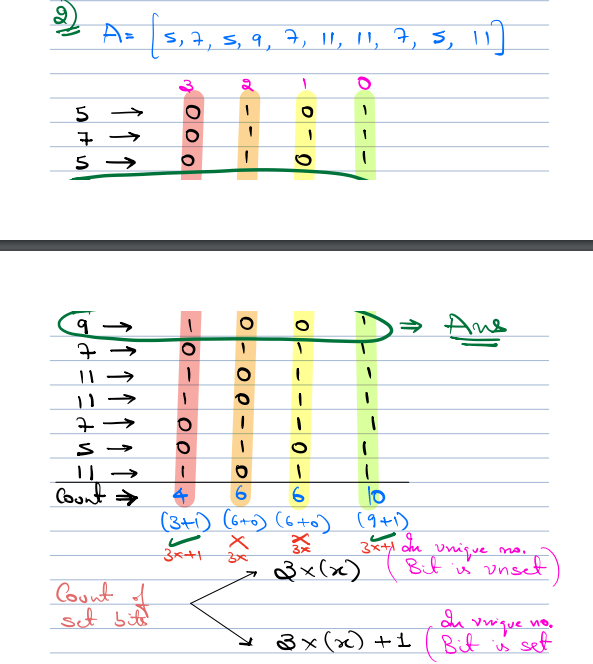
Iterate on every bit.
If the count of numbers in which ith bit is set is a multiple of 3, then in answer ith bit is NOT SET.
If the count of numbers in which ith bit is of the form (3 * x) + 1, then in answer ith bit is SET.

Pseudocode¶

int ans = 0;

for (int i = 0; i < 32; i++) { // go to every bit one by one  
    int cnt = 0;

    for (int j = 0; j < arr.size(); j++) { // iterate on array

        // check if ith bit is set
        if ((arr[j] & (1 << i)) cnt++;
        }

        if (cnt % 3 == 1) // If the count is not the multiple of 3
            ans = ans | 1 << i; // set ith bit in ans
    }

    print(ans);

Complexity¶

Time Complexity: O(N)
Space Complexity: O(1)

Problem 3 Single number 3¶

Given an integer array, all the elements will occur twice except two. Find those two elements.

Input:

[4, 5, 4, 1, 6, 6, 5, 2]

Output:

1, 2

Hint:¶

Will finding XOR help ? May be!
What do we get if we XOR all numbers ? XOR of the two unique numbers!
From that can we identify/separate the two numbers ? Not Really! Why?
- Example: If XOR is 7, we aren't sure which 2 numbers are they. (2, 5), (1, 6), (3, 4), ... have xor = 7, so we won't be able to identify!

Is there any way in which we can identify the two numbers from their XOR ?

Suppose if two unique numbers are a and b. Their XOR is c.

In c if say 0^th bit is set, what does that tell about a and b ?

In one of the numbers the bit is set and in other the bit is unset! So, can we identify the numbers based on that ?

Idea:¶

We will find the position of any set bit in XOR c, it will denote that this bit is different in a and b.
Now, we divide the entire array in two groups, based upon whether that particular bit is set or not.
This way a and b will fall into different groups.
Now since every number repeats twice, they will cancel out when we take XOR of the two groups individually leaving a and b.

Pseudocode¶

int xorAll = 0;

// XOR of all numbers in the array
for (int i = 0; i < N; i++) {
    xorAll ^= A[i];
}

// Find the rightmost set bit position
// Note: Any other bit can be used as well
int pos;

for (pos = 0; pos < 32; pos++) {
    if (checkbit(xorAll, pos))
        break;
}

num1 = 0;
num2 = 0;

// Divide the array into two groups based on the rightmost set bit
for (int i = 0; i < N; i++) {
    if (checkbit(A[i], pos)) {
        num1 ^= A[i];
    } else {
        num2 ^= A[i];
    }
}

print(num1);
print(num2);

Question¶

What is the time complexity to find two unique elements where every element is present 2 times except for two unique elements?

Choices

O(1)
O(log(N))
O(N)
O(32 * N)

Problem 4 Maximum AND pair¶

Given N array elements, choose two indices(i, j) such that (i != j) and (arr[i] & arr[j]) is maximum.

Input:

[5, 4, 6, 8, 5]

Output:

[0, 4]

If we take the & of 5 with 5, we get 5 which is the maximum possible value here. The required answer would be their respective indices i.e. 0,4

Question¶

Max & Pair in this array (arr[] = 21,18,24,17,16) is

Choices

21&17
24&21
17&16
24&18

Question¶

Max & Pair in this array (arr[] =5,4,3,2,1) is

Choices

5&4
1&2
1&4
4&3

Warning

Please take some time to think about the solution approach on your own before reading further.....

Maximum AND pair Approach¶

Brute Force¶

Using two for loops and calculating bitwise & for all possible pairs and storing the maximum of all of them.

Complexity¶

Time Complexity: O(N^2)
Space Complexity: O(1)

Observation¶

When bit is set in both the numbers, that bit in their & will be 1
For answer to be maximum, we will want the set bit to be present towards as left as possible.
This indicates that we should start processing the numbers from MSB.

Optimized Solution¶

Iterate from the Most significant bit to Least significant bit and for all the numbers in the array, count the numbers for which that bit is set
If the count comes out to be greater than 1 then pairing is possible, so we include only the elements with that bit set into our vector. Also, set this bit in your answer.
If the count is 0 or 1, the pairing is not possible, so we continue with the same set and next bit position.

Dry Run¶

Example: { 26, 13, 23, 28, 27, 7, 25 }

26: 1 1 0 1 0
13: 0 1 1 0 1
23: 1 0 1 1 1
28: 1 1 1 0 0
27: 1 1 0 1 1
07: 0 0 1 1 1
25: 1 1 0 0 1

Let's start with MSB, at position 4, there are 5 numbers with set bits. Since count is >=2, we can form a pair. Therefore, in answer 1 will be present at this position. ans:

1	_	_	_	_

We will remove all numbers where 0 is present. [13 and 7 gets removed or are set to 0]

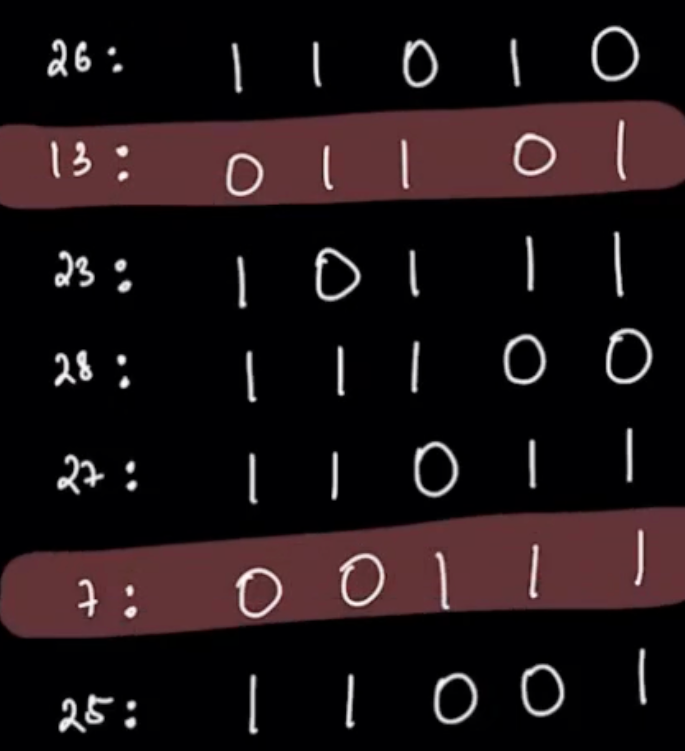
At position 3, there are 4 numbers with set bits(which haven't been cancelled). Since count is >=2, we can form a pair. Therefore, in answer 1 will be present at this position. ans:

1	1	_	_	_

We will remove all numbers where 0 is present. [23 gets removed or is set to 0]

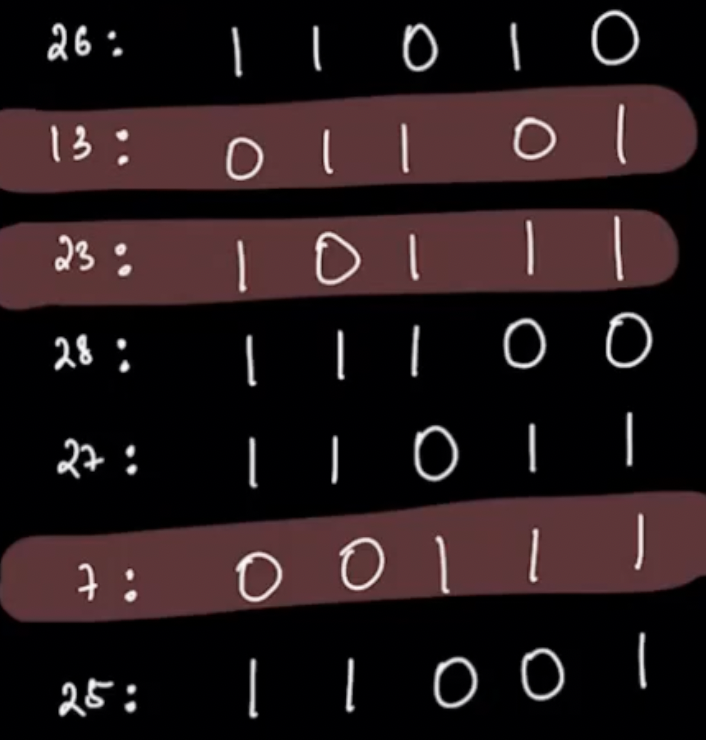
At position 2, there is 1 number with set bit. Since count is less than 2, we can't form a pair. Therefore, in answer 0 will be present at this position.

ans:

1	1	0	_	_

We will NOT remove any number.

At position 1, there are 2 numbers with set bits. Since count is >=2, we can form a pair. Therefore, in answer 1 will be present at this position.

ans:

1	1	0	1	_

We will remove all numbers where 0 is present. [28 and 25 gets removed or are set to 0]

At position 0, there is 1 number with set bit. Since count is <2, we can't form a pair. Therefore, in answer 0 will be present at this position.

ans:

1	1	0	1	0

We will NOT remove any number.

We are done and answer final answer is present in variable ans.

Maximum AND pair Pseudocode¶

Pseudocode¶

 int ans = 0;

 for (int i = 31; i >= 0; i--) {
     //count no. of set bits at ith index
     int count = 0;

     for (int j = 0; j < n; j++) {
         if (arr[j] & (1 << i))
             cnt++;
     }

     //set that bit in ans if count >=2
     if (count >= 2) {
         ans = ans | (1 << i);

         //set all numbers which have 0 bit at this position to 0
         for (int j = 0; j < n; j++) {
             if (arr[j] & (1 << i) == 0)
                 arr[j] = 0;
         }

     }
 }

 print(ans);

//The numbers which cannot be choosen to form a pair have been made zero

Complexity¶

Time Complexity: O(N)
Space Complexity: O(1)

Similarly, if we have to find maximum & of triplets then we will do for count>=3 and for quadruples as count >= 4 and so on ...

Problem 5 Count of pairs with maximum AND¶

Calculate the Count of Pairs for which bitwise & is maximum (GOOGLE Interview Question)

Solution:¶

Do exactly as above and then traverse on the array and find the number of elements which are greater than 0

Required answer will be Nc2 or N(N-1)/2

Complexity¶

Time Complexity: O(N)
Space Complexity: O(1)