DSA: Graphs 2: BFS, Matrix Questions & Topological Sort¶
BFS¶
Breadth-First Search (BFS) is another graph traversal algorithm used to explore and navigate graphs or trees. It starts at a source node and explores all its neighbors at the current depth level before moving on to the next level. BFS uses a queue data structure to maintain the order of nodes to be visited.
Approach:¶
- We use a queue to maintain the order of nodes to visit in a breadth-first manner.
- We start with a vector visited to keep track of whether each node has been visited. Initially, all nodes are marked as unvisited (false).
- We enqueue the startNode into the queue and mark it as visited.
- We enter a loop that continues until the queue is empty.
- In each iteration, we dequeue the front element (the current node) from the queue and process it. Processing can include printing the node or performing any other desired operation.
- We then iterate through the neighbors of the current node. For each neighbor that hasn't been visited, we enqueue it into the queue and mark it as visited.
- The BFS traversal continues until the queue is empty, visiting nodes level by level.
Example/Dry-Run¶
A --- B --- C
| |
+---------+
|
D
- Start from the source node (City A).
- Explore neighboring nodes level by level.
- Use a queue to maintain the order.
- Mark visited nodes (using adjaency list) to avoid repetition.
- Stop when the target node (City D) is reached.
- This guarantees the shortest path in unweighted graphs.
Pseudocode:¶
void bfs(int startNode) {
vector < bool > visited(MAX_NODES, false); // Initialize all nodes as unvisited
queue < int > q;
q.push(startNode); // Enqueue the start node
visited[startNode] = true; // Mark the start node as visited
while (!q.empty()) {
int currentNode = q.front();
q.pop();
// Process the current node (e.g., print or perform an operation)
for (int neighbor: graph[currentNode]) {
if (!visited[neighbor]) {
q.push(neighbor); // Enqueue unvisited neighbors
visited[neighbor] = true; // Mark neighbor as visited
}
}
}
Compexity¶
Time Complexity: O(V + E)
Space Complexity: O(V)
Question¶
Consider a graph with the following adjacency matrix:
[0, 1, 1, 0]
[1, 0, 0, 0]
[1, 0, 0, 1]
[0, 0, 1, 0]
What is the order in which the nodes will be visited when performing a breadth-first search (BFS) starting from node 0?
Choices
- 0, 1, 2, 3
- 0, 1, 3, 2
- 0, 2, 3, 1
- 0, 1, 3, 1
The correct answer is (a) 0, 1, 2, 3.
BFS (Breadth-First Search) explores neighbor nodes first before moving to the next level. Starting from node 0, BFS visits its neighbors 1 and 2. It then moves to the next level and visits 1's neighbor 3. Finally, it moves to the next level but finds no more unvisited nodes. Therefore, the order of BFS traversal is 0, 1, 2, 3.
Multisource BFS¶
There are N number of nodes and multisource(S1,S2,S3), we need to find the length of shortest path for given destination node to any one of the source node{S1,S2,S3}.
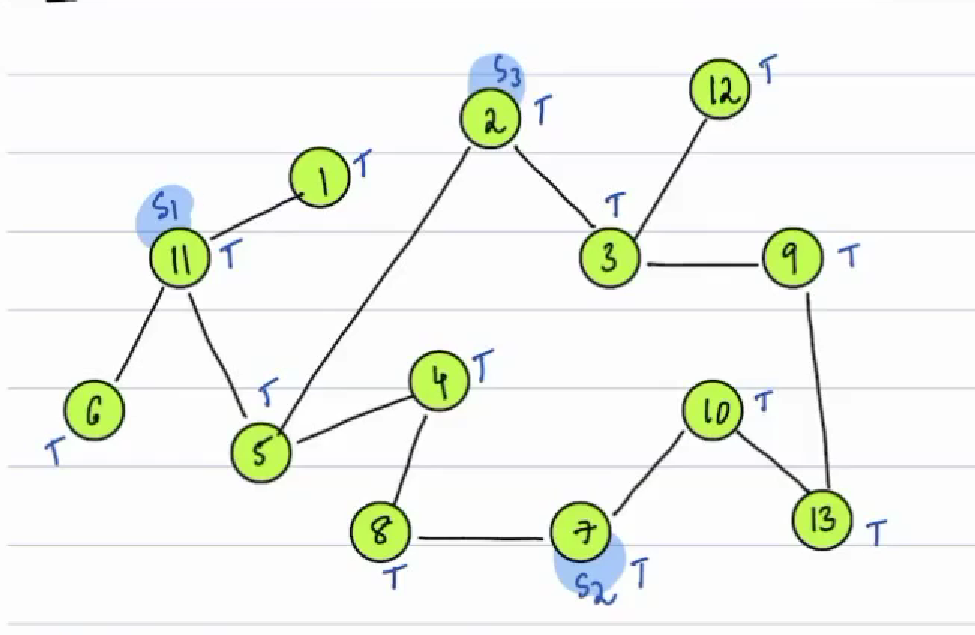
Solution¶
Length = 2
In the beginning, we need to push all source node at once and apply exact BFS,then return the distance of destination node.
Time and Space Complexity¶
- TC - O(N+E)
- SC - O(N+E)
Rotten Oranges¶
There is given a matrix and there are 3 values where 0 means empty cell, 1 means fresh orange present and 2 means rotten orange prsent, we need to find the time when all oranges will become rotten.
Note: If not possible, return - 1.
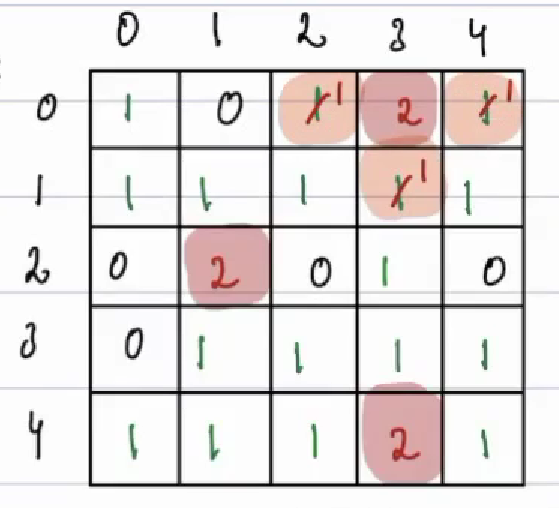
Solution¶
Answer: after 3 minutes all oranges will get rotten.
- Initially, We need to insert all rotten oranges in Queue (where each element in queue is in a pair),
- Then check if any fresh oranges has become rotten and if they did, return the time otherwise return -1.
Pseudocode¶
public class RottingOranges {
private static final int[] dx = {-1, 1, 0, 0};
private static final int[] dy = {0, 0, -1, 1};
public int orangesRotting(int[][] grid) {
int rowCount = grid.length;
int colCount = grid[0].length;
Queue< int[] > queue = new LinkedList< >();
int freshOranges = 0;
int minutes = 0;
// Count fresh oranges and add rotten oranges to the queue
for (int i = 0; i < rowCount; i++) {
for (int j = 0; j < colCount; j++) {
if (grid[i][j] == 2) {
queue.offer(new int[]{i, j, minutes});
} else if (grid[i][j] == 1) {
freshOranges++;
}
}
}
if (freshOranges == 0) {
// If there are no fresh oranges initially, they are already rotten.
return 0;
}
while (!queue.isEmpty()) {
int[] cell = queue.poll();
int x = cell[0];
int y = cell[1];
minutes = cell[2];
for (int i = 0; i < 4; i++) {
int newX = x + dx[i];
int newY = y + dy[i];
if (isValid(grid, newX, newY) && grid[newX][newY] == 1) {
grid[newX][newY] = 2;
freshOranges--;
queue.offer(new int[] {newX, newY, minutes + 1});
}
}
}
return (freshOranges == 0) ? minutes : -1;
}
private boolean isValid(int[][] grid, int x, int y) {
int rowCount = grid.length;
int colCount = grid[0].length;
return x >= 0 && x < rowCount && y >= 0 && y < colCount;
}
Possibility of finishing the courses¶
Given N courses with pre-requisites, we have to check if it is possible to finish all the course ?
Example:
N = 5
Pre-requisites
1 ---> 2 & 3 [1 is pre-req for 2 and 3]
2 ---> 3 & 5
3 ---> 4
4 ---> 2
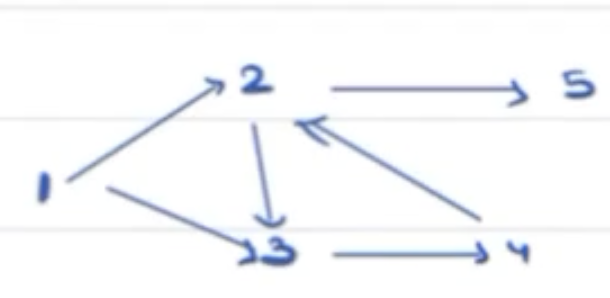
The pre-req information is represented in above directed graph.
Explanantion:¶
Que: Which course shall we complete first?
The one having no pre-requisites. (say 1)
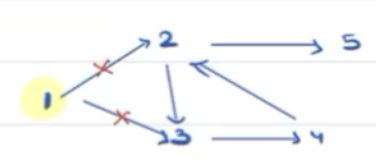
Next, which one shall we pick ?
We can't pick any course because of the dependencies. Hence, it means we can't finish courses in above example.
The reason is there's a cycle!
Have you heard of the term deadlock ? [For experience we need job, for job we need experience like scenario :p ]
Conclusion: If it's a cyclic graph, answer will always be false, else true.
Observation: To solve the problem, we need directed acyclic graph!
Possibility of finishing courses approach¶
Warning
Please take some time to think about the solution approach on your own before reading further.....
Example:
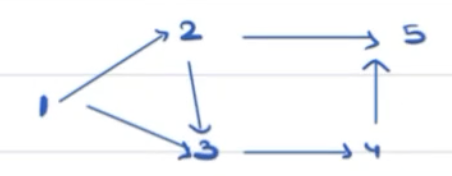
Pick ? 1 [not dependant on any other course]
Next Pick ? 2
Next Pick ? 3
Next Pick ? 4
Next Pick ? 5
Order:
1 2 3 4 5
The above order is known as topological sort/ topological order.
Que: For one graph, can we have only one topological order?
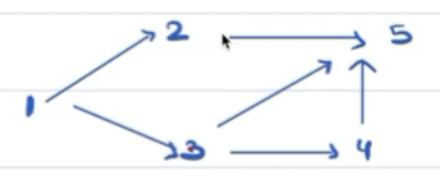
Is the order 1 2 3 4 5 valid ? YES!
What about 1 3 2 4 5 ? YES!
What about 1 3 4 2 5 ? YES!
Hence, it is possible that we have multiple topological order for a given graph.
Definition¶
Topological sort is a linear ordering of the vertices (nodes) in a directed acyclic graph (DAG) such that for every directed edge (u, v), vertex u comes before vertex v in the ordering. In other words, it arranges the nodes in such a way that if there is a directed edge from node A to node B, then node A comes before node B in the sorted order.
Topological Sort¶
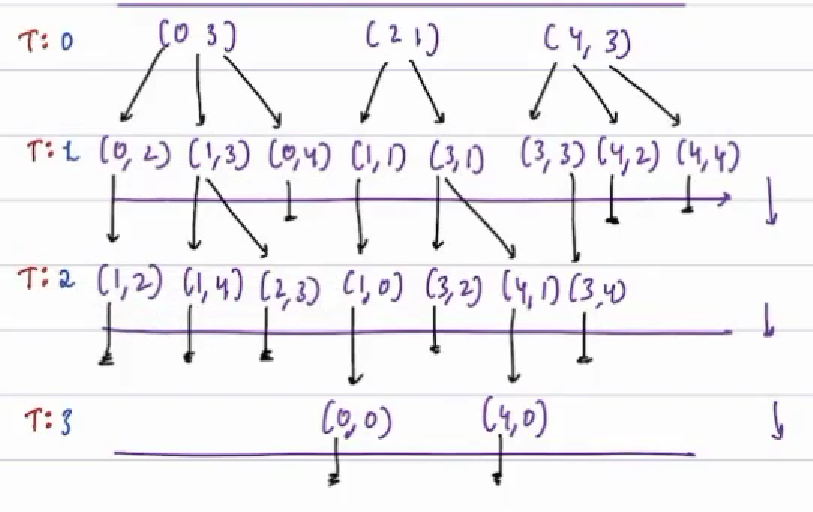
Let's find topological ordering of below graph!
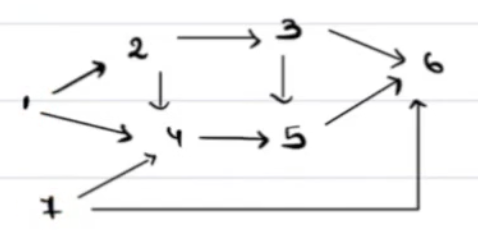
Indegree: The count of incoming nodes is known as indegree of a node.
For above graph, the indegrees will be as follows -
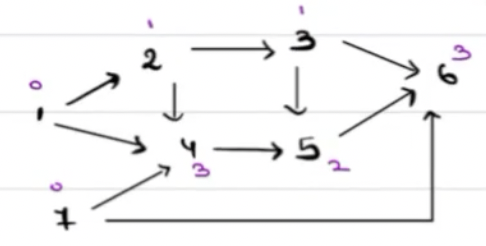
Next Steps¶
- Insert all the nodes with indegree=0 in a queue
- Dequeue an element from the queue and update the indegree for all the neighbours, if the indegree for any nbr becomes 0 add that node in the queue.
Approach:¶
- Create an array to store indegrees, initially set all values to zero.
- Iterate through each node in the graph using a loop.
- For each node, traverse its outgoing edges by iterating through its adjacency list.
- For each neighboring node in the adjacency list, increment its indegree count by one.
- Continue the loop until you've processed all nodes in the graph.
- The array now contains the indegree of each node, where the value at index i represents the indegree of node i.
Example:
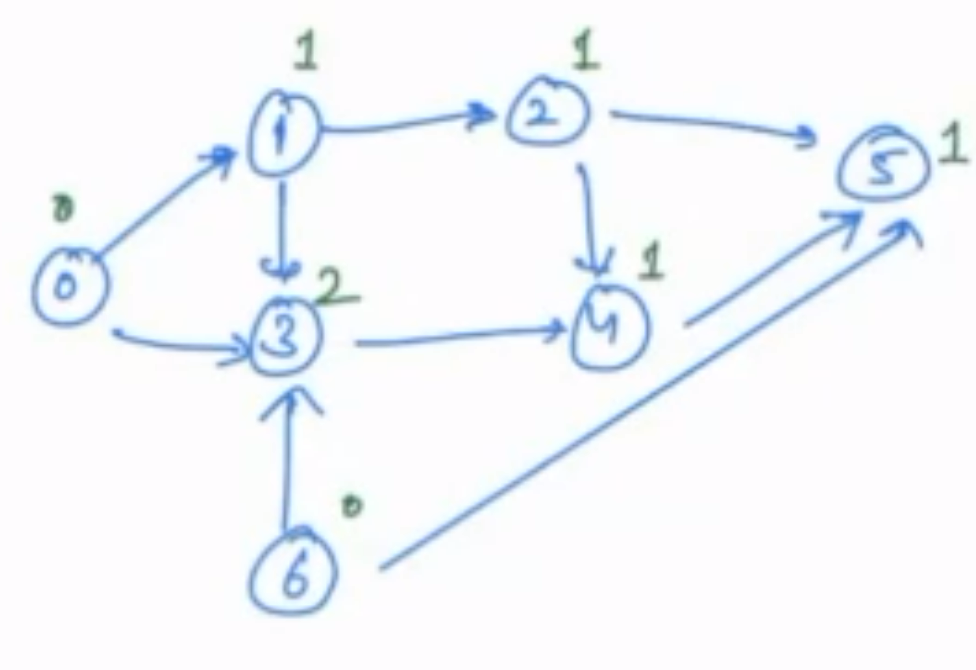
In the above photo we can refer the indegree of each of the nodes is written in green.
Pseudocode:¶
in [N], i, in [i] = 0;
for (i = 0; i < n; i++) {
for (nbr: adj[i]) {
ibr[i] += 1;
}
}
Complexity¶
Time Complexity: O(N + E)
Space Complexity: 0(N)
Topological Sort (Right to Left)¶
In a right-to-left topological order, you start from the "rightmost" vertex (i.e., a vertex with no outgoing edges) and proceed leftward. This approach can be useful in certain situations and can be thought of as a reverse topological ordering.
Here's how you can approach it:
Approach:¶
- Identify a vertex with no outgoing edges (in-degree = 0). If there are multiple such vertices, you can choose any of them.
- Remove that vertex from the graph along with all its outgoing edges. This removal may affect the in-degrees of other vertices.
- Repeat steps 1 and 2 until all vertices are removed from the graph. The order in which you remove the vertices constitutes the right-to-left topological order.
Example/Dry-Run:¶
A -> B -> C
| |
v v
D E
To find the right-to-left topological order:
- Start with a vertex with no outgoing edges. In this case, you can start with vertex C.
- Remove vertex C and its outgoing edge. The graph becomes:
A -> B
|
v
D E
Now, you can choose either B or E, both of which have no outgoing edges. Let's choose B and remove it:
A
|
v
D E
- Continue with the remaining vertices. Choose A next:
|
v
D E
- Finally, remove D and E:
|
v
| |
The order in which you removed the vertices is a right-to-left topological order: C, B, A, D, E.
Pseudocode¶
function topologicalSortRightToLeft(graph):
// Function to perform DFS and record nodes in the order they are finished
function dfs(node):
mark node as visited
for each neighbor in graph[node]:
if neighbor is not visited:
dfs(neighbor)
append node to order list
create an empty order list
initialize a visited array with False for all nodes
for each node in the graph:
if node is not visited:
dfs(node)
reverse the order list
return the reversed order list as the topological order (right-to-left)
Complexity¶
Time Complexity: O(V+E)
Space Complexity: O(V)
Question¶
Which of the following is correct topological order for this graph?
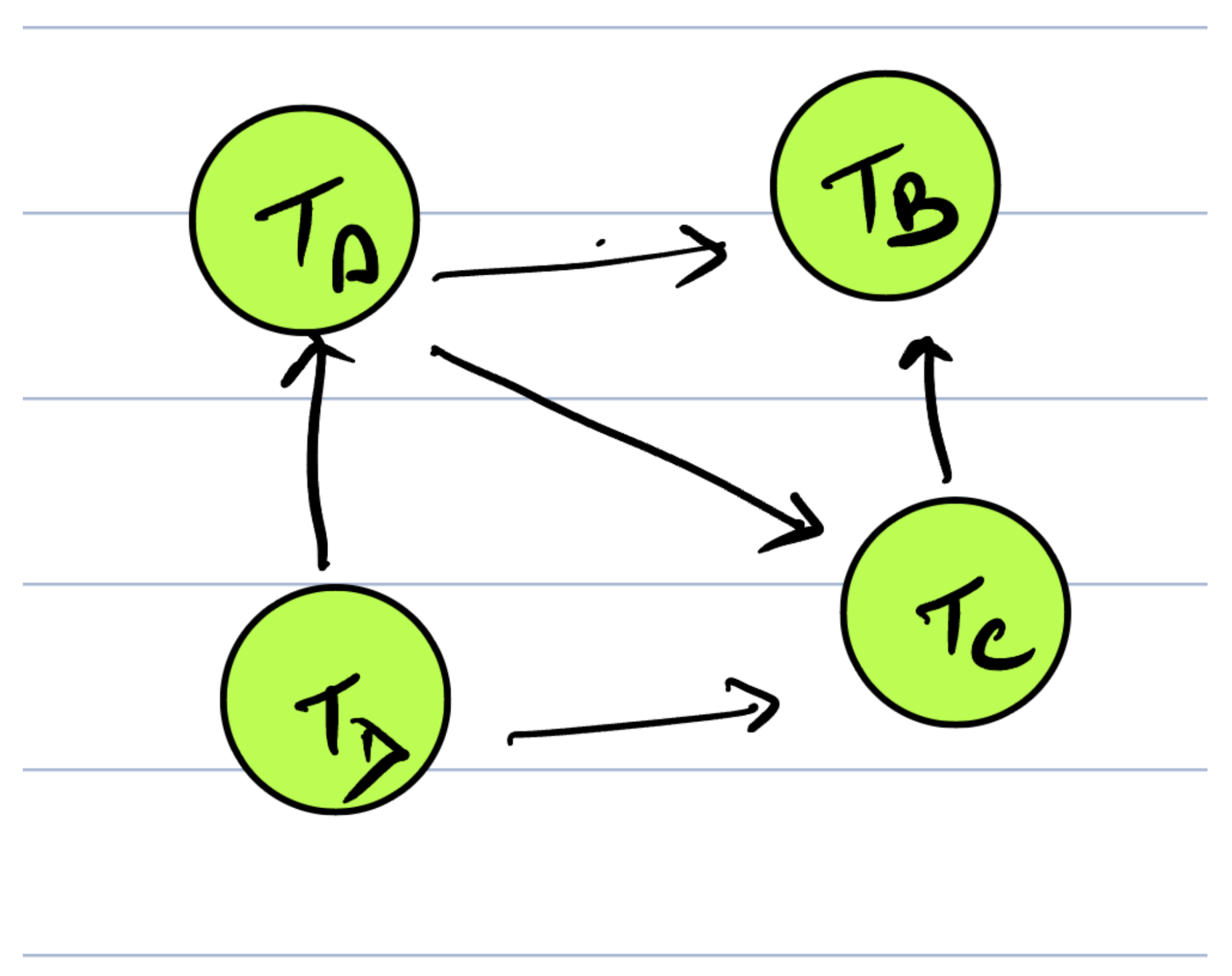
Choices
- TD,TA,TC,TB
- TA,TD,TC,TB
- TC,TA,TD,TB
Another approach to BFS¶
Find the minimum number of edges to reach v starting from u in undirected simple graph.
Graph:
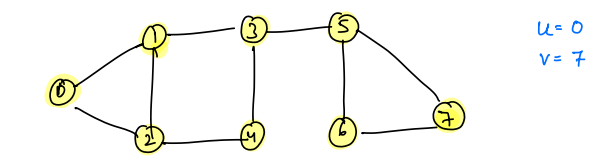
Approach¶
Imagine you're playing a game where you have to find the quickest way from point A (vertex u) to point B (vertex v) in a giant maze. This is similar to using Breadth-First Search (BFS) in a graph.
Think of BFS as your strategy for exploring the maze:
Start at Point A: You're at the entrance of the maze (vertex u), ready to find the shortest path to the treasure (vertex v).
Explore Closest Paths First: Just like deciding which paths to take in the maze, BFS first checks all the paths that are one step away from your current position, then moves to paths two steps away, and so on.
Layer by Layer: It's like a ripple effect in a pond. You throw a stone (start at vertex u), and the ripples (paths) expand outward, reaching further away points one layer at a time.
Reaching Point B: As you follow this method, the moment you step on point B (vertex v) in the maze, you know you've found the shortest route. In BFS, when you first reach vertex v, it guarantees the minimum steps taken, just like finding the quickest path out of the maze.
So, by using BFS in our maze game (or graph), we ensure we're taking the most efficient route possible, avoiding any long detours or dead-ends. It's a smart and systematic way to reach our goal with the least amount of hassle!
