DP 4: Applications of Knapsack¶

Question¶

Time Complexity of the unbounded 0-1 knapsack problem?

W : capacity of knapsack
N : no. of elements
K : Max weight of any item
P : max value of any item

Choices

Chose the correct answer

Explanation

For every node, we need to go to its left, that's the only way we can reach the smallest one.

Introduction to the knapsack and DP¶

What Is Dynamic Programming?¶

In the context of dynamic programming, the knapsack problem refers to a classic optimization problem that can be solved using dynamic programming techniques.

Example¶

Suppose we are working on solving the fibonacci series problesm, then we can break it into step by step as follows:

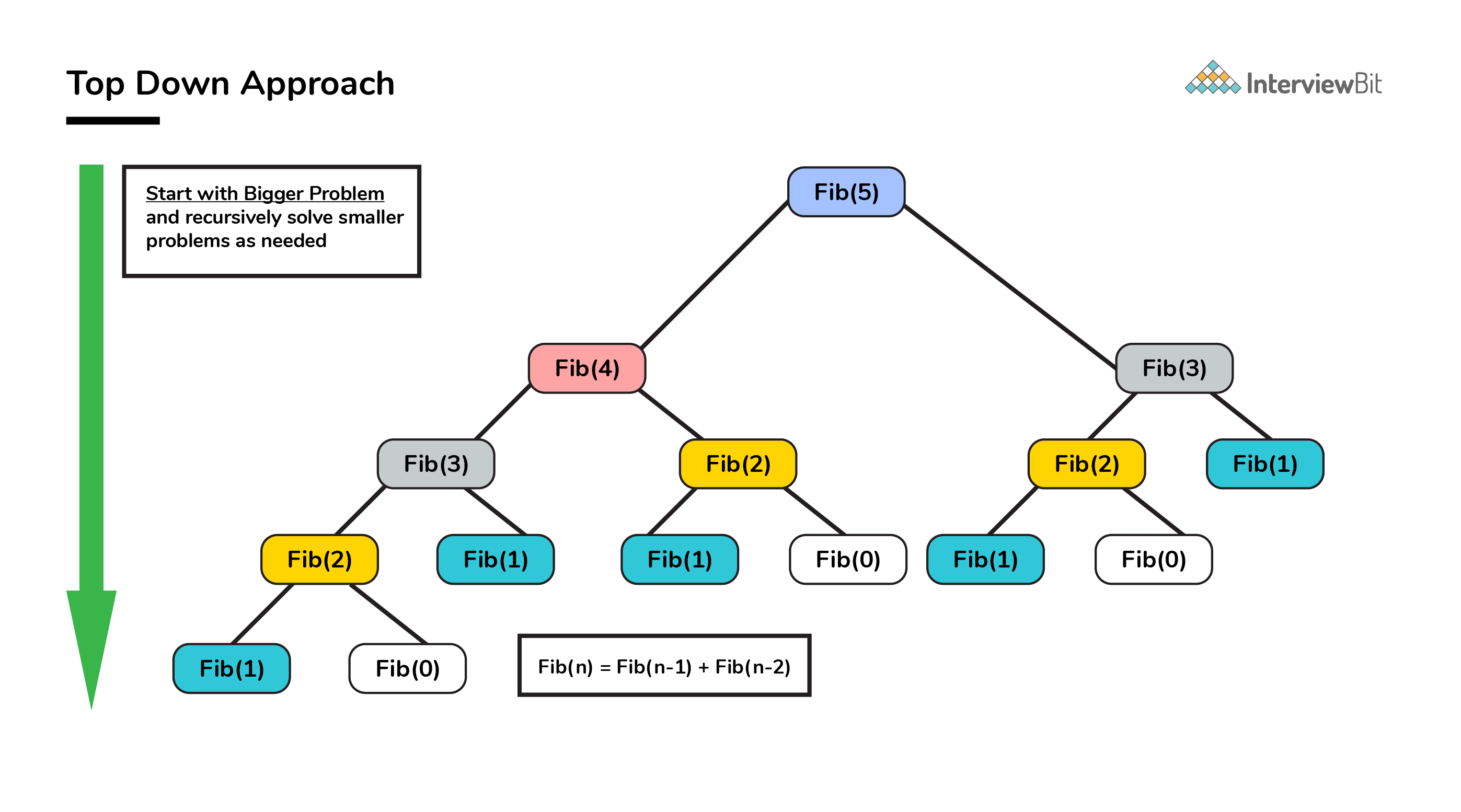
Let us now solve some questions related to dynamic programming.

Problem 1 Cut the rod for maximum profit¶

A rod of length N and an array A of length N is given. The elements (i) of the array contain the length of the rod (1-based indexing). Find the maximum values that can be obtained by cutting the rod into some pieces and selling them.

Example

Suppose we have the length on N = 5 and we have to divide it then the division can be done as:

Now, we can see that 9 is the maximum value that we can get.

Solution¶

A naive approach to solving this problem would involve considering all possible combinations of cutting the rod into pieces and calculating the total value for each combination. This can be achieved using recursion and backtracking, where for each possible cut, the value of the cut piece is added to the recursively calculated value of the remaining part of the rod. The maximum value obtained among all combinations is the desired result.

Warning

Please take some time to think about the solution approach on your own before reading further.....

Our Approach¶

As we can visualize from the example, there is an overlapping subproblem and an optimal sub-structure. So, we should opt for the DP approach.

Note: We can observe three things here:

1. The maximum capacity is the length of the order.
2. `A[i]` is storing the length of the piece of the rod.
3. The sum of the length of each piece must be less than or equal to ``N``

The general observation that we can get here from these three things is that it is a knapsack problem.

Question¶

The cutting rod question is:

Choices

Fractional Knapsack
0-1 Knapsack
Unbounded Knapsack (or 0-N Knapsack)

Cut the rod for maximum profit Approach¶

Approach¶

First, define the state of the dp i.e. dp[i], it will be the maximum value that can be received by the rod of length i.
The base case will be 0 in the case when the length of the rod is 0. This means dp[0] = 0.

We will loop over the array, and then calculate the maximum profit, and finally store the maximum profit in the current dp state.

Let us now see the pseudo-code for the problem.

Pseudocode¶

for all values of i: dp[i] = 0

for (i = 1 to N) // length of rod to sell = i
{
    for (j = 1 to i) {
        dp[i] = max(dp[i], A[j] + dp[i - j])
    }
}
return dp[N]

Time and Space Complexity¶

Time Complexity: \(O(N^2^)\), as we are traversing the N-length array using nested for loops (Simply, we can also say that the capacity is N and the length of the array is also N).
Space Complexity: O(N), as we are using an extra dp array to store the current state of profit.

Problem 2 Count the number of ways using coins (ordered selection)¶

In how many ways can the sum be equal to N by using coins given in the array? One coin can be used multiple times.

Example

There are 2 ways to solve this problem

a. Ordered selection of coin

Let us create the set of numbers that cummulate the value of N.

So, we can see that we have the value we get is 6.

Now, let's look at the selection tree of the coin selection. We can divide the number by selecting the choices of subraction.

Solution - Ordered Selection of Coin¶

The naive approach to solving this problem involves using a recursive approach with backtracking. For each coin value in the array, subtract it from the target sum N, and recursively find the number of ways to form the remaining sum using the same coin set. Repeat this process for all coins and sum up the results.

Warning

Please take some time to think about the solution approach on your own before reading further.....

Approach¶

As we can observe from the examples above, we have to calculate the number of ways of selection, it is similar to the unbounded knapsack problem (as one coin can be selected multiple times).

Question¶

What is the number of ways to get sum = 0

Choices

0
1
2
Undefined

Count the number of ways using coins Pseudocode¶

Pseudocode¶

for all values of i: dp[i] = 0
dp[0] = 1

for (i = 1 to N) {
    for (j = 1 to(A.length - 1)) {
        if (A[j] <= i) {
            dp[i] += dp[i - A[j]]
        }
    }
}

return dp[N]

Time and Space Complexity¶

Time Complexity: \(O(N * (length~ of ~the ~array))\).
Space Complexity: \(O(N)\).

Problem 3 Count the number of ways using coins (un-ordered selection)¶

Given a set of coins and a target sum, find the number of ways to make the target sum using the coins, where each coin can only be used once.

Example

Suppose we have a situation same as the last one.
N = 5 and coins we have [3, 1, 4].

So here we have 3 possible ways.

Now, let us try to arrage the coins to get the desired value.

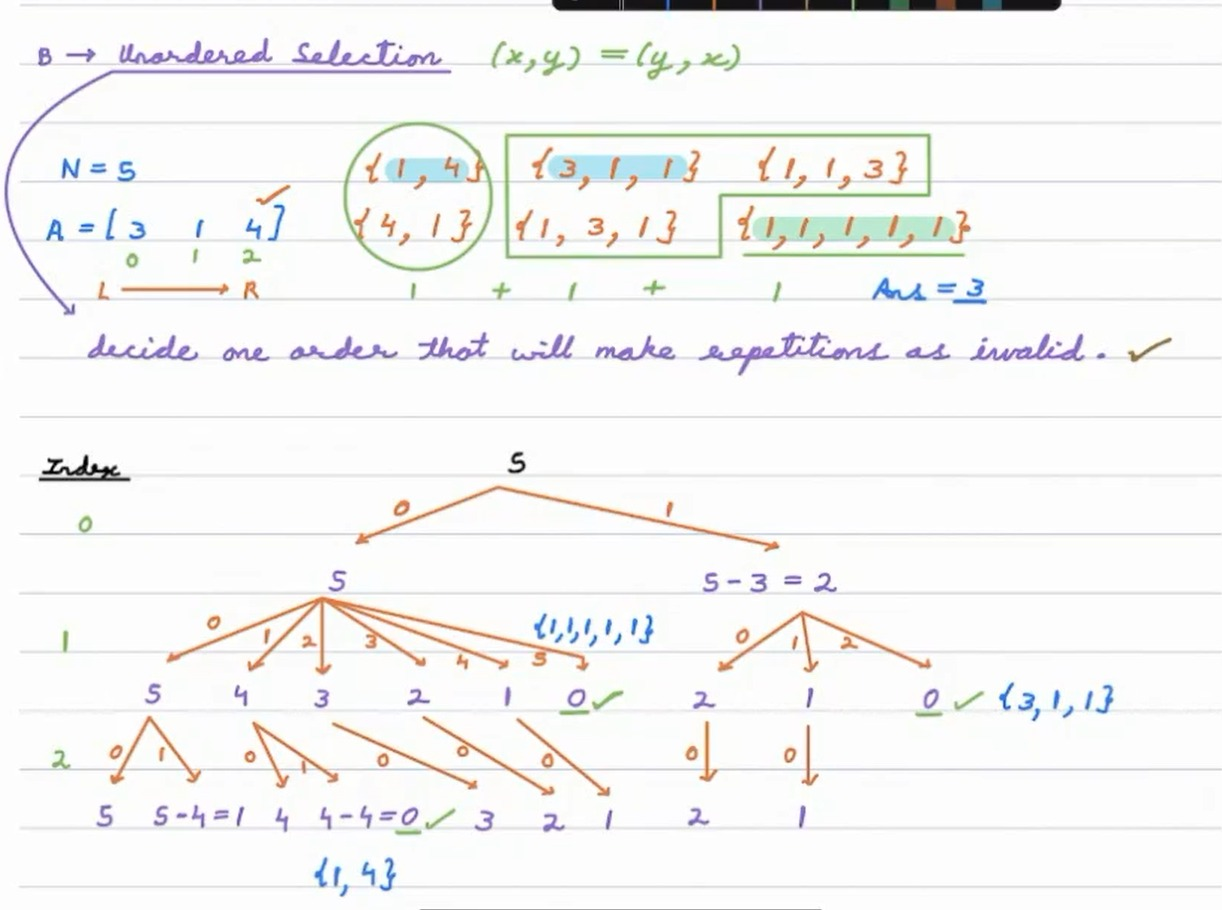
So, what we can observe out of it is:

The current state of dp, i.e. dp[i] is to select the number of ways to get the sum equal to i by selecting coins from L to R in the array.

Warning

Please take some time to think about the solution approach on your own before reading further.....

Solution: Un-ordered Selection of Coin¶

How we can solve it:

Initialize an array dp with all values set to 0. This array will be used to store the number of ways to make change for each possible sum from 0 to N.
Set the initial value of dp[0] to 1. This step indicates that there is one way to make change for an amount of 0, which is by not using any coins.
Iterate through the different coin denominations represented by the array A. This loop will consider each coin one by one.
For each coin denomination A[j], iterate through the possible sums from 1 to N. This loop will consider each sum value from 1 to N and calculate the number of ways to make change for that sum.
Inside the inner loop, check if the current coin denomination A[j] is less than or equal to the current sum i. If it is, then it's possible to use this coin to make change for the current sum.
If the condition is met, update the dp array for the current sum i by adding the number of ways to make change for the remaining amount (i - A[j]). This is where dynamic programming comes into play, as you are building up the solutions for larger sums based on the solutions for smaller sums.
After both loops complete, the dp[N] value will represent the number of ways to make change for the desired amount N using the given coin denominations.
Finally, return the value stored in dp[N].

Pseudocode¶

for all values of i: dp[i] = 0
dp[0] = 1

for (j = 0 to(A.length - 1)) // coins
{
    for (i = 1 to N) // sum
    {
        if (A[j] <= i) {
            dp[i] += dp[i - A[j]]
        }
    }
}

return dp[N]

Time and Space Complexity¶

Time Complexity: \(O(N * (length~ of~ the~ array))\).
Space Complexity: O(N).

Problem 4 Extended 0-1 Knapsack Problem¶

We are given N toys with their happiness and weight. Find max total happiness that can be kept in a bag with the capacity W. Here, we cannot divide the toys.

The constraints are:

\(- 1 <= N <= 500\)
\(- 1 <= h[i] <= 50\)
\(- 1 <= wt[i] <= 10^9\)
\(- 1 <= W <= 10^9\)

Question¶

What is the MAX value we can get for these items i.e. (weight, value) pairs in 0-1 knapsack of capacity W = 8.
Items = [(3, 12), (6, 20), (5, 15), (2, 6), (4, 10)]

Chose the correct answer

Choices

27
28
29
30

Explanation

Simple 0-1 Knapsack, after trying all combinations 27 is the highest value we can have inside the knapsack.

Extended 0-1 Knapsack Problem Approach and Explanation¶

Approach and Calculations¶

The normal approach to solve this problem would involve using a recursive or iterative algorithm to consider all possible combinations of toys and select the one with the maximum happiness that doesn't exceed the weight limit. However, due to the constraints provided (N up to 500, wt[i] up to \(10^9\), W up to \(10^9\)), this approach would be extremely slow and inefficient.

By employing dynamic programming, we can optimize the solution significantly. The DP approach allows us to break down the problem into subproblems and store the results of these subproblems in a table to avoid redundant calculations. In this case, we can use a 2-D DP table where dp[i][w] represents the maximum happiness that can be achieved with the first i toys and a weight constraint of w.

DP offers a much faster solution, as it reduces the time complexity from exponential to polynomial time, making it suitable for large inputs like those in the given constraints. Therefore, opting for a DP approach is essential to meet the time and pace constraints of this problem.