DP 3: Knapsack¶
Knapsack Problem¶
Given N objects with their values Vi profit/loss their weight Wi. A bag is given with capacity W that can be used to carry some objects such that the total sum of object weights W and sum of profit in the bag is maximized or sum of loss in the bag is minimized.
We will try Knapsack when these combinations are given:
- number of objects will be N
- every object will have 2 attributes namingly value and weight
- and capacity will be given
Problem 1 Fractional Knapsack¶
Given N cakes with their happiness and weight. Find maximum total happiness that can be kept in a bag with capacity = W (cakes can be divided)
Example:
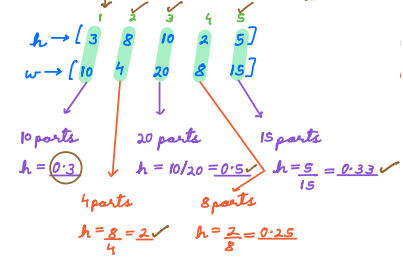
N = 5; W = 40
Happiness of the 5 cakes = [3, 8, 10, 2, 5]
Weight of the 5 cakes = [10, 4, 20, 8, 15]
Goal - happiness should be maximum possible and the total sum of weights should be <= 40.
Warning
Please take some time to think about the solution approach on your own before reading further.....
Approach
Since we can divide the objects, hence they can be picked based on their value per unit weight.
For per unit weight, below are the happiness values:
- Cake 1:
happiness = 0.3; - Cake 2:
happiness = 2; - Cake 3:
happiness = 0.5; - Cake 4:
happiness = 0.25; - Cake 5:
happiness = 0.33;
Solution
Arrange the cakes in descending order with respect to happiness/weight and start picking the element
- Select the 2nd cake (happiness = 2), reducing capacity to 36(40-4).
- Choose the 3rd cake (happiness = 0.5), further reducing capacity to 16(36-20).
- Opt for the 5th cake (happiness = 0.33), leaving a capacity of 1(16-15).
- Take a part of the 1st cake (happiness = 0.3), using up the remaining capacity.
- Total happiness achieved: 23.3 (8 + 10 + 5 + 0.3).
Time complexity of the above solution is O(Nlog(N)) because it requires sorting with respect to happiness/weight.
Space complexity of the above solution is O(1).*
Pseudo Code¶
public class Solution {
class Items {
double cost;
int weight, value, ind;
Items(int weight, int value, double cost) {
this.weight = weight;
this.value = value;
this.cost = cost;
}
}
public int solve(int[] A, int[] B, int C) {
Items[] iVal = new Items[A.length];
for (int i = 0; i < A.length; i++) {
double cost = (A[i] * 1.0) / B[i];
iVal[i] = new Items(B[i], A[i], cost);
}
Arrays.sort(iVal, new Comparator < Items > () {
@Override
public int compare(Items o1, Items o2) {
if (o1.cost >= o2.cost) {
return -1;
}
return 1;
}
});
double totalValue = 0.0;
for (int i = 0; i < A.length; i++) {
int curWt = iVal[i].weight;
int curVal = iVal[i].value;
if (C >= curWt) {
C = C - curWt;
totalValue += curVal;
} else {
totalValue += (C * iVal[i].cost);
break;
}
}
return (int)(totalValue * 100);
}
}
Flipkart's Upcoming Special Promotional Event¶
Flipkart is planning a special promotional event where they need to create an exclusive combo offer. The goal is to create a combination of individual items that together offer the highest possible level of customer satisfaction (indicating its popularity and customer ratings) while ensuring the total cost of the items in the combo does not exceed a predefined combo price.
Problem 2 : 0-1 Knapsack¶
0-1 Knapsack¶
In this type of knapsack question, division of object is not allowed.
Question¶
Given N toys with their happiness and weight. Find maximum total happiness that can be kept in a bag with capacity W. Division of toys are not allowed.
Question¶
In the Fractional Knapsack problem, what is the key difference compared to the 0/1 Knapsack?
Choices
- Items can only be fully included or excluded.
- Items can be partially included, allowing fractions.
- The knapsack has infinite capacity.
- The knapsack has a fixed capacity.
Explanation
In the Fractional Knapsack problem, items can be included in fractions, enabling optimization of the total value based on weight.
Example:
N = 4; W = 7
Happiness of the 4 toys = [4, 1, 5, 7]
Weight of the 4 toys = [3, 2, 4, 5]
If we buy toys based on maximum happiness or maximum happiness/weight we may not get the best possible answer.
Warning
Please take some time to think about the bruteforce approach on your own before reading further.....
Brute Force Approach:¶
- Consider all subsets of items and select the one with highest summation of happiness.
Since there are in total 2N subsequences and we have to consider each of them. Therefore the time complexity is: 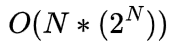
Dry Run of Brute Force Apporach¶

In the above figure each element is taken and its selection is determined based on happiness and weight.
Here we can notice optimal sub structure as well as overlapping sub problems.
Thus we can use dynamic progamming in this case
If index and capacity can define one unique state total number of unique states are O(N * (W + 1)) which is O(N * W), as index will go from 0 to N - 1 and weight will go from 0 to W.
dp[N][W] = max happiness (considering N objects and capacity W)
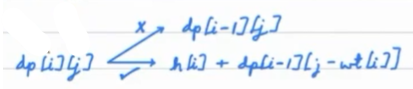
Here taking N = i and W = j, we have two choices either to select dp[i][j] or to reject it. On selecting it will result into
h[i] + dp[i - 1][j - wt[i]](h[i]=happiness of i) and on rejecting it will bedp[i - 1][j].
Base Case¶
- for all j when i = 0, dp[0][j] = 0
- for all i when j = 0, dp[i][0] = 0
Psuedocode¶
//for all i,j dp[i][j]=0
for (i--> 1 to N) { // 1based index for input
for (j--> 1 to W) {
if (wt[i] <= j) {
dp[i][j] = max(dp[i - 1][j], h[i] + dp(i - 1)(j - wt[i]))
} else {
dp[i][j] = dp[i - 1][j]
}
}
}
return dp[N][w]
}
The dimensions should be (N + 1) * (W + 1) as the final answer would be at dp[N][W]
Dry run¶
taking the N = 4 and W = 7
Happiness of the 4 toys = [4, 1, 5, 7]
Weight of the 4 toys = [3, 2, 4, 5]
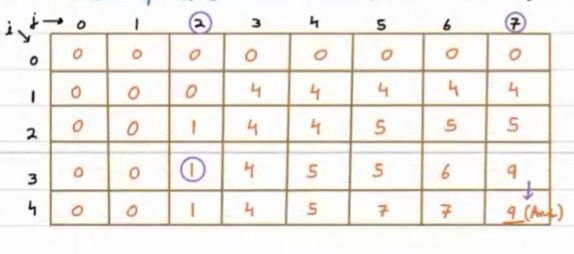
- Initially, we filled the
dpmatrix with zeros. Now, we will fill every position one by one.- At i = 1, j = 1
wt[i] = wt[1] = 3
since wt[i] > j, dp[i][j] = dp[i - 1][j] => dp[1][1] = dp[0][1] = 0
- At i = 1, j = 1
- At i = 1, j = 2
wt[i] = wt[1] = 3
since wt[i] > j, dp[i][j] = dp[i - 1][j] => dp[1][2] = dp[0][2] = 0 - At i = 1, j = 3
wt[i] = wt[1] = 3
since wt[i] <= j, dp[i][j] = max(dp[i - 1][j], h[i] + dp[i - 1][j - wt[i]]) => dp[1][3] = max(dp[0][2], h[1] + dp[0][0]) = max(0, 4 + 0) = 4
Similary we wil follow the above to fill the entire table.
Time complexity for the above code is O(N * W)
Space Complexity for the above code is O(N * W), we can furture optimize space complexity by using 2 rows. So the space complexity is O(2W) which can be written as O(W).
Problem 3 Unbounded Knapsack¶
Unbounded Knapsack or 0-N Knapsack¶
- objects cannot be divided
- same object can be selected multiple times
Question¶
Given N toys with their happiness and weight. Find more total happiness that can be kept in a bag with capacity W. Division of toys are not allowed and infinite toys are available.
Example¶
N = 3; W = 8
Happiness of the 3 toys = [2, 3, 5]
Weight of the 3 toys = [3, 4, 7]
In this case we will select second index toy 2 times. Happiness we will be 6 and weight will be 8.
Now here as we do not have any limitation on which toy to buy index will not matter, only capacity will matter.
Warning
Please take some time to think about the brute force approach on your own before reading further.....
Dry Run for Brute Force Appoarch¶
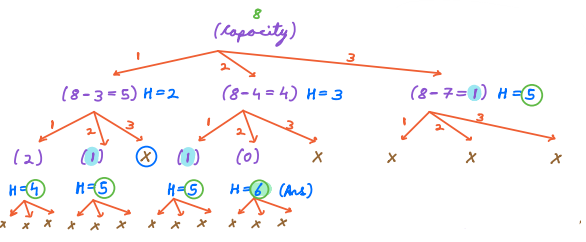
Step 1:
- if we select toy with index 1, capacity left will be
8 - wt of toy 1 = 8 - 3 = 5. And the happiness will beh = 2 - Similarily if we select toy with index 2, capacity left will be
8 - wt of toy 2 = 8 - 4 = 4. And the happiness will beh = 3 - if we select toy with index 3, capacity left will be
8 - wt of toy 3 = 8 - 7 = 1. And the happiness will beh = 5
Step 2: After buying toy 1
- Now if we buy toy 1, capacity will reduce to 2 and happiness will become 4
- Similary if we buy toy 2, capacity will reduce to 1 and happiness will become 5
- We cannot buy toy 3 as the capacity will be exceeded.
We will follow similar steps to find all the possiblity.
We will pick the toy with maximum happiness that is 6 in this case after selecting toy 2 firstly and then selecting toy 2 again.
Here we can notice optimal sub structure as well as overlapping sub problems. Thus we can apply dynamic programming.
- Unqiue states here will be
W + 1 = O(W)because the capacity can be from 0 to W
Base case for the above question:
- if capacity is 0, happiness is 0. So,
dp[0] = 0
Equation dp[i] = max(h[i] + dp[i - wt[j]]) for all toys j
Psuedocode¶
for all i, dp[0] = 0
for (i--> 1 to W) {
for (j--> 1 to N) {
if (wt[j] <= i)
dp[i] = max(h[i] + dp[i - wt[j]])
}
}
return dp[W]
Complexity¶
Time Complexity: O(N * W)
Space Complexity: O(W)
Question¶
We have Weight Capacity of 100
- Values = {1, 30}
- Weights = {1, 50}
What is the maximum value you can have?
Choices
- 0
- 100
- 60
- 80
Explanation
There are many ways to fill knapsack.
- 2 instances of 50 unit weight item.
- 100 instances of 1 unit weight item.
- 1 instance of 50 unit weight item and 50 instances of 1 unit weight items.
We get maximum value with option 2, i.e 100
