DP 1: One Dimentional¶

Fibonacci Series¶

0 1 1 2 3 5 8 13 21 ...

fibonacci Expresion¶

fib(n) = fib(n-1) + fib(n-2)
base case for the fibonacci expression -> fib(0) = 0; fib(1) = 1

Psuedocode¶

int fib(n) {
    if (n <= 1) return n;
    return fib(n - 1) + (n - 2);
}

Time complexity for the above code : O(2^N)
Space Complexity for the above code : O(N)

Problem 1 Fibonacci Series¶

Properties of Dynamic Programming¶

Optimal Substructure - i.e. solving a problem by solving smaller subproblems
Overlapping Subproblems - solving some subproblems multiple times

Solution for Dynamic Programming¶

Store the information about already solved sub-problem and use it

Psuedocode of Fibonacci series using dynamic Programming¶

int f[N + 1] // intialize it with -1

int fib(n) {
    if (N <= 1) return n;

    // if already solved, don't repeat
    if (f[N] != -1) return f[N];

    // store it
    f[N] = fib(n - 1) + (n - 2);
    return f[N];
}

Two main operations performed in the above code of dynamic programming:

If we have already solved a problem just return the solution, don't repeat the step
If not solved, solve and store the solution

Dry Run¶

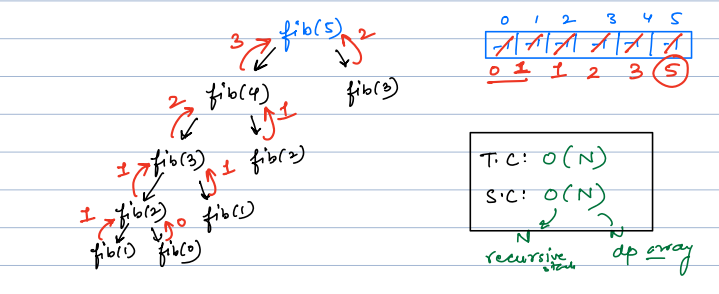
We're going to figure out what fib(5) is using a method called recursion, and we'll keep track of our answers in an array. Here's how it works, step by step:

Starting Point:

We want to find out what fib(5) is. Our array, where we store our results, starts with -1 in every spot because we haven't calculated anything yet.

Breaking it Down:

To get fib(5), we first need to know fib(4) and fib(3).

Going Deeper:

For fib(4), we need fib(3) and fib(2). And for fib(3) (the one we saw earlier), we also need fib(2) and fib(1).

Even Deeper:

To find fib(2), we look at fib(1) and fib(0).

Simple Answers:

Now, fib(1) and fib(0) are easy; they are 1 and 0. We use these to find out fib(2), which is 1 (0 + 1). Store it before moving forward.

Building Up:

We keep using these small answers to find the bigger ones. If we already know an answer (like fib(2)), we don't have to calculate it again; we just use the answer from our array.

By the end, we'll have the answer to fib(5), and all the smaller fib numbers stored in our array!

Time and Space Complexity¶

Time Complexity for the above code is O(N) and space complexity is O(N). Thus, we were able to reduce the time complexity from O(2^N) to O(N) using dynamic programing

Dynamic Programming Types¶

Types of DP Solution:¶

Dynamic programming solution can be of two types:

Top-Down [Also know as Memoization]
- It is a recursive solution
- We start with the biggest problem and keep on breaking it till we reach the base case.
- Then store answers of already evaluated problems.
Bottom-Up
- It is an iterative solution
- We start with the smallest problem, solve it and store its result.
- Then we keep on moving to the bigger problems and use the already calculated results from sub-problems.

Bottom Up Approach for Fibonacci series¶

Psuedocode¶

int fib[N + 1];

fib[0] = 0;
fib[1] = 1;

for (i = 2, i <= N; i++) {
    fib[i] = fib[i - 1] + fib[i - 2];
}

Complexity¶

Time Complexity: O(N)
Space Complexity: O(N)

Through this approach we were able to eliminate recursive stack.

Further optimising the Space Complexity¶

If seen closely, the above approach can be optimised by using just simple variables instead of an array. In this way, we can further optimize the space.

Pseudocode¶

int a = 0;
int b = 1;
int c;
for (int i = 2; i <= N; i++) {
    c = a + b;
    a = b;
    b = c;
}

In the above code we were able to optimize the space complexity to O(1).

Question¶

What is the purpose of memoization in dynamic programming?

Choices

To minimize the space complexity of the algorithm
To store and reuse solutions to subproblems
To calculate results of all calls
To improve the readability of the code

Question¶

Which approach is considered as an iterative process?

Choices

Top-down approach
Bottom-up approach
Both are iterative
Neither is iterative

Problem 2 Climbing Staircase¶

Calculate the number of ways to reach the Nth stair. You can take 1 step at a time or 2 steps at a time.

CASE 1: (number of stairs = 1) {1}

Number of ways to reach first stair : 1 (as shown in fig)

CASE 2: (number of stairs = 2)

{1, 1}

Number of ways to reach two stairs : 2 (as shown in fig)

CASE 3: (number of stairs = 3)

{1, 2}
{1, 1, 1}

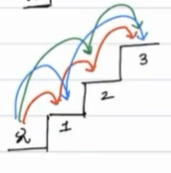
Number of ways to reach two stairs : 3 (as shown in fig)

CASE 4: (number of stairs = 4)

{1, 1, 2}
{2, 2}
{1, 2, 1}
{1, 1, 1, 1}

Question¶

In Stairs Problems, the result for N=4

Choices

4
5
6
7

Explanation:

To reach 1^st staircase : 1 way
To reach 2^nd staircase : 2 ways
To reach 3^rd staircase : 3 ways
To reach 4^th staircase : 5 ways

Warning

Please take some time to think about the solution approach on your own before reading further.....

Problem 2 Climbing Staircase Approach¶

Approach¶

We can come to 4^th stair from 2^nd and 3^rd step.

If I get to know #steps to reach stair 3, we can take length 1 step and reach stair 4.
Similarly, if I get to know #steps to reach stair 2, we can take length 2 step and reach stair 4.

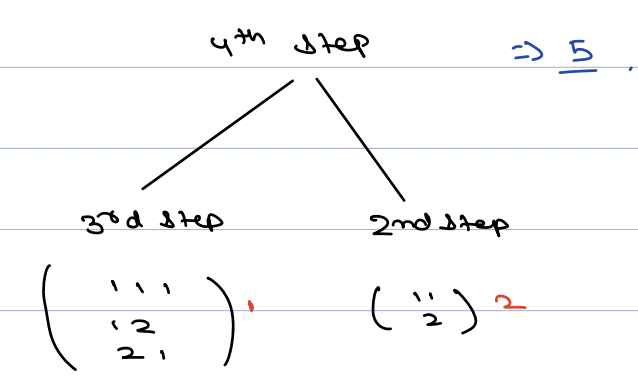
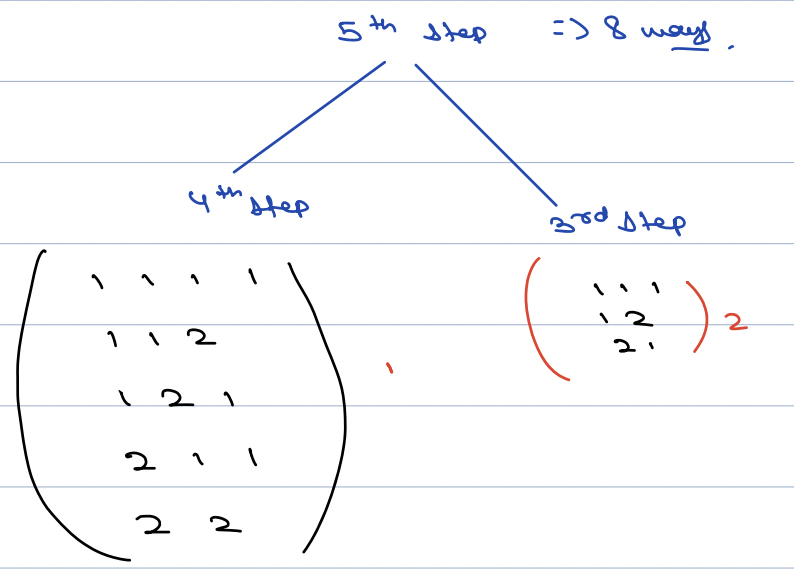
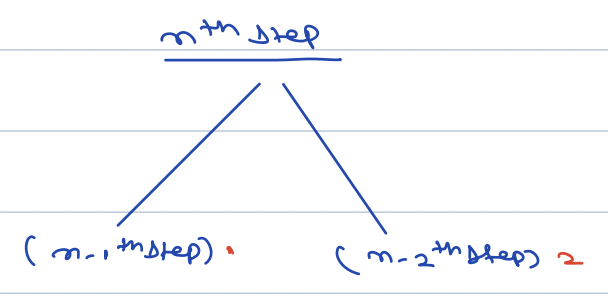
Number of ways we can reach to the nth step is either by (n - 1) or (n - 2).
Answer will be summation of number of ways to reach (n - 1)th step + number of ways to reach (n - 2)th step

We can see that the above has been deduced to fibonacii expression

Problem 3 Get Minimum Squares¶

Find minimum number of perfect squares required to get sum = N. (duplicate squares are allowed)

example 1 → N = 6

sum 6 can be obtained by the addition of following squares:

1^2+1^2+1^2+1^2+1^2+1^2
1^2+1^2+2^2 → minimum number of squares is 3 in this case

example 2 → N = 10

sum 10 can be obtained by the addition of following squares:

1^2+1^2+..... 10 times
2^2 + 1^2..... 6 times
2^2 + 2^2 + 1^2 + 1^2
3^2 + 1^2→ minimum number of squares is 2 in this case

example 3 → N = 9

sum 10 can be obtained by the addition of following squares:

1^2+1^2+..... 9 times
2^2 + 1^2..... 5 times
2^2 + 2^2 + 1^2
3^2 → minimum number of squares is 1 in this case

Question¶

What is the minimum number of perfect squares required to get sum = 5. (duplicate squares are allowed)

Choices

5
1
2
3

Explanation:

sum 5 can be obtained by the addition of following squares:

1^2 + 1^2 + 1^2 + 1^2 + 1^2
2^2 + 1^2 → minimum number of squares is 2 in this case

Warning

Please take some time to think about the solution approach on your own before reading further.....

Get Minimum Squares Approach¶

Approach 1¶

Can we simply do N - (nearest perfect square) ?
- Verifying approach 1 with example N=12
- 12-9 (closest square) = 3
- 3-1 = 2
- 2-1 = 1
- 1-1 = 0
- We are using 4 perfect squares, whereas the minimum number of square is 3 (2^2 + 2^2 +2^2) so approach 1 is not useful in this case

Brute Force Approach¶

Try every possible way to form the sum using brute force to solve a example N = 12

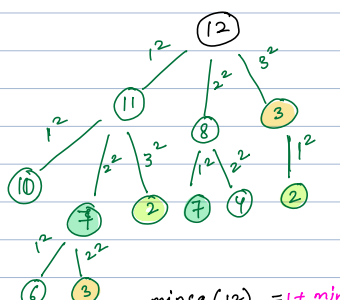
The above image shows all possiblities to achieve 12.

Now, to get minimum sum of 12 we will find minimum square of 11 or minimum square of 8 or minimum square of 3 + 1.

The above is a recursive problem where we can see overalapping subproblems, like for N=7.

Dynamic Programming Approach¶

Here optimal structure has been obtained as well as overlapping subproblems

So, we can say that square(i) = 1 + min{ squares(i - x^2) for all x^2 <= i}and base case is square[0] = 0

Psuedocode¶

int dp[N + 1]; //initialise (-1)
int psquares(int N, int dp[]) {
    if (n == 0) return 0;
    if (dp[N] != -1) return dp[N];
    ans = int - max;
    for (x = 1; x * x <= N; x++) {
        ans = min(ans, psquares(N - x ^ 2)); // dp
    }
    dp[N] = 1 + ans;
    return dp[N];
}

Time complexity for the above code is O(N(sqrt(N))) and space complexity is O(N).