DP 2: Two Dimensional¶
Problem 1 Maximum Subsequence Sum¶
Find maximum subsequence sum from a given array, where selecting adjacent element is not allowed.
Examples
Example 1: ar[] = {9, 4, 13}
Output 1: 22. Since out of all possible non adjacent element subsequences, the subsequence (9, 13) will yield maximum sum.
Example 2: ar[] = {9, 4, 13, 24}
Output 2: 33 (24 + 9)
Question¶
Find maximum subsequence sum from [10, 20, 30, 40], where selecting adjacent element is not allowed.
Choices
- 70
- 60
- 100
- 50
Explanation:
Maximum Subsequence is 60. Since, Out of all possible non adjacent element subsequences, the subsequence (20, 40) will yield maximum sum of 60.
Maximum Subsequence Sum Brute Force Approach¶
Warning
Please take some time to think about the brute force approach on your own before reading further.....
Brute Force Approach¶
- Consider all the valid subsequences
(this a backtracking step). - For creating subsequences, for every element we can make a choice, whether to select it or reject it.
- Say, we start from right most element. If we keep it, then (n - 1)th element can't be considered, so jump to (n - 2)th. If we don't, then (n - 1)th element can be considered. So on...
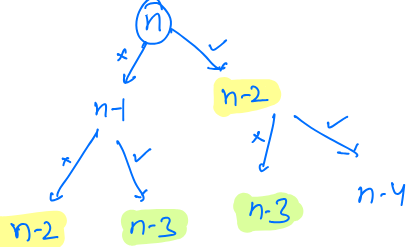
The above image shows tree which has all the choices of selection. Here we can see that the choices are overlapping.
Moreover, as the problem can be broken into smaller problems and has overlapping sub problems, we can use dynamic programming.
Maximum Subsequence Sum Top Down Approach¶
Top Down Approach¶
So for maxSum(i) there are two options:
- either we can select element present at index i
- if we select that element we will include its value ie ar[i] and the recursive call will be maxSum(i-2)
- or we cannot select the element present at index i
- so in this case we will not include its value and will make recursive call which is maxSum(i-1)
dp[i] = stores the maximum value that can be obtained by selecting 0 to ith toy.
The maximum of the choice we make will give us the final answer
Psuedocode¶
int dp[N] //initialize it with negative infinity
// i will be initialised with N-1, i.e we start with the last element
int maxSum(int[] arr, i, dp[N]) {
if (i < 0) {
return 0
}
if (dp[i] != -infinity) {
return dp[i]
}
//Don't consider the ith element, in this case we can consider (i-1)th element
f1 = maxSum(arr, i - 1, dp);
//Consider the ith element, in this case we can't consider (i-1)th element, so we jump to (i-2)th element
f2 = arr[i] + maxSum(arr, i - 2, dp);
ans = max(f1, f2)
dp[i] = ans;
return ans
}
Time & Space Complexity¶
Time complexity: O(N). As we are filling the DP array of size N linearly, it would take O(N) time. Space complexity: O(N), because of dp array of size N.
Maximum Subsequence Sum Bottom Up Approach¶
Problem 1
dp[i] is defined as the maximum subsequence sum from [0 - i] provided no adjacent elements are selected
arr = {9, 4, 13, 24}
We can start from arr[0] and we have two choices: either we can select arr[0] or reject.
- If we select it, the maximum value we can acheive is arr[0] = 9
- If we reject it, the value which we will get is 0
-
So, we will store arr[0] in dp[0]
-
Now, we will look at arr[0] and arr[1] to find the maximum
- As arr[0] > arr[1], we will store arr[0] in dp[1]
- Similary we will repeat the above steps to fill dp[].
Psuedocode¶
dp[N]
for(i = 0; i < N; i++){
dp[i] = max(dp[i - 1], arr[i] + dp[i - 2])
}
return dp[N - 1]
Time & Space Complexity¶
Time complexity: O(N). As we are filling the DP array of size N linearly, it would take O(N) time.
Space complexity: O(N), because of dp array of size N.
Problem 2 Count Unique Paths¶
Given mat[n][m], find total number of ways from (0,0) to (n - 1, m - 1). We can move 1 step in horizontal direction or 1 step in vertical direction.
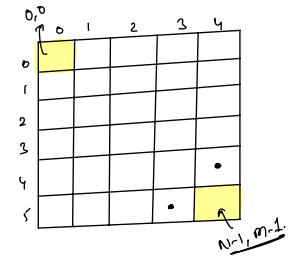
Example
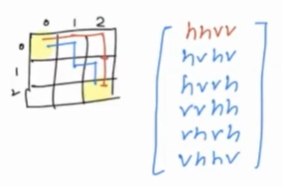
hrepresents movement in horizontal direction andvrepresents movement in vertical direction
Ans: 6
Question¶
Find the total number of ways to go from (0, 0) to (1, 2)
| o | ||
|---|---|---|
| o |
Choices
- 1
- 2
- 3
- 4
Explanation:
The 2D matrix dp is
| 0 | 1 | 2 | |
|---|---|---|---|
| 0 | 1 | 1 | 1 |
| 1 | 1 | 2 | 3 |
From here, the number of ways to go from (0, 0) to (1, 2) is 3.
Count Unique Paths Brute Force Approach¶
Warning
Please take some time to think about the solution approach on your own before reading further.....
Brute Force Appoarch¶
Backtracking, i.e., start from (0, 0) and try all possible scenarios to reach (n - 1, m - 1)
Observation¶
Can we break it into subproblems?
- We can reach (n - 1, m - 1) in one step (by moving vertically) from (n - 2, m - 1)
- We can reach (n - 1, m - 1) in one step (by moving horizontally) (n - 1, m - 2)
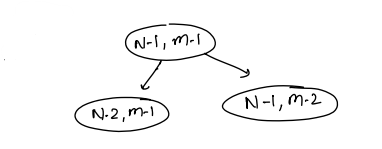
Recursive Relation¶
ways(i, j) = ways(i - 1, j) + ways(i, j - 1)
Base Condition¶
- When i == 0, we have only one path to reach at the end, i.e., by moving vertically.
- Similary, when j == 0, we have only one path to reach at the end, i.e., by moving horizontally.
Therefore, ways(0, j) = ways(i, 0) = 1
Pseudocode:¶
int ways(i, j) {
if (i == 0 || j == 0) {
return 1;
}
return ways(i - 1, j) + ways(i, j - 1);
}
Time Complexity: O(2 ^ (N * M)), as at every step we have two options, and there are total of N * M cells.
Count Unique Paths Optimization¶
Optimization using DP¶
We can see the optimal substructure in this problem as it can be defined in terms of smaller subproblems.
Are there overlapping subproblems as well?
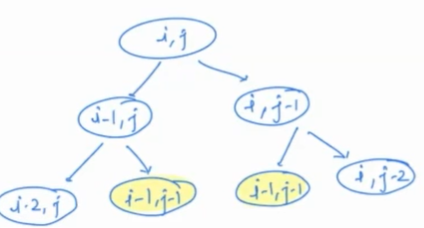
We can see that, (i - 1, j - 1) are the overlapping subproblems.
Since there is optimal substructure and overlapping subproblems, DP can be easily applied.
Which type of array should be used?
Since two args (i and j) are varying in above method, 2-d storage is needed of size N x M.
Top Down Approach¶
dp[i][j] = It is defined as the total ways to reach from 0,0 to i,j
Pseudocode¶
int dp[N][M]; // initialized with -1
int ways(i, j) {
if (i == 0 || j == 0) {
return 1;
}
if (dp[i][j] != -1) {
return dp[i][j];
}
ans = ways(i - 1, j, dp) + ways(i, j - 1, dp);
dp[i][j] = ans;
return ans;
}
Complexity¶
Time Complexity: O(N * M), as we are filling a matrix of size N * M.
Space Complexity: O(N * M), as we have used dp matrix of size N * M.
In how many ways can we reach (0, 0) starting from (0, 0)?
If you say 0, that means there is no way to reach (0, 0) or (0, 0) is unreachable. Hence, to reach (0, 0) from (0, 0), there is 1 way and not 0.
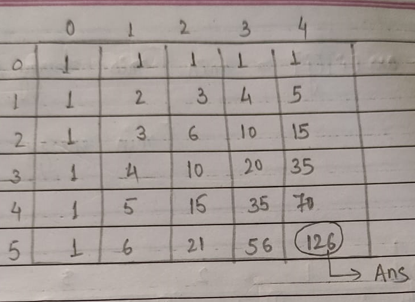
Bottom Up Approach:¶
Consider a 2D matrix dp of size N * M.
dp[i][j] = It is defined as the total ways to reach from 0,0 to i,j
In bottom up approach, we start from the smallest problem which is (0, 0) in this case.
- No. of ways to move (0, 0) from (0, 0) = ways(0, 0) = 1
- Similarly, ways(0, 1) = ways(0, 2) = . . . = 1
- Also, ways(1, 0) = ways(2, 0) = . . . = 1
- Now, ways(1, 1) = ways(1, 0) + ways(0, 1) = 2
- Similarly, ways(1, 2) = ways(1, 1) + ways(0, 2) = 3, and so on.
Pseudocode¶
dp[N][M];
// Initialize `dp` row - 0 and col - 0 with 1.
for (i = 1; i <= N; i++) {
for (j = 1; j <= M; j++) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[N - 1][M - 1];
Time Complexity: O(N * M)
Space Complexity: O(N * M)
Can we further optimize the space complexity?¶
- The answer of every row is dependent upon its previous row.
- So, essentially, we require two rows at a time - (1) current row (2) previous row. Thus, the space can be optimized to use just two 1-D arrays.
Problem 3 Total number of ways to go to bottom right corner from top left corner¶
Find the total number of ways to go to bottom right corner (N - 1, M - 1) from top left corner (0, 0) where cell with value 1 and 0 represents non-blocked and blocked cell respectively.
We can either traverse one step down or one step right.

Solution¶
| 1 | 1 | 1 | 1 |
|---|---|---|---|
| 1 | 0 | 1 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 2 |
| 0 | 0 | 1 | 3 |
The given problem is just a variation of above problem. Only advancement is that if cell value has 0, then there is no way to reach the bottom right cell.
Warning
Please take some time to think about the solution approach on your own before reading further.....
Pseudocode (Recursive Approach)¶
if (mat[i][j] != 0) {
ways(i, j) = ways(i - 1, j) + ways(i, j - 1);
} else {
ways[i][j] = 0;
}
Similar base condition can be added to top-down and bottom-up approach to optimize it using DP.
Question¶
How many unique paths in the grid from (0, 0) to (2, 2) ?
| 1 | 1 | 1 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
where cell with value 1 and 0 represents non-blocked and blocked cell respectively.
Choices
- 0
- 1
- 2
- 3
Explanation:
On the Grid, Row 1 is completely blocked. So there is no path from (0, 0) to (2, 2).
Thus, the Total number of unique paths is 0.
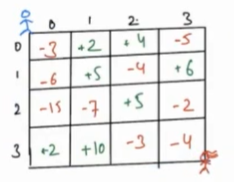
Problem 4 Dungeons and Princess¶
Find the minimum health level of the prince to start with to save the princess, where the negative numbers denote a dragon and positive numbers denote red bull.
Redbull will increase the health whereas the dragons will decrease the health.
The prince can move either in horizontal right direction or vertical down direction. If health level <= 0, it means prince is dead.
Warning
Please take some time to think about the solution approach on your own before reading further.....
Observation¶
One might argue to solve it by finding the path with minimum sum or maximum sum.
Let's check does it even work or not?
Using path with minimum sum(fails)¶
- For the above matrix, the path with minimum sum is -3 -> -6 -> -15 -> -7 -> 5 -> -3 -> -4, which yields sum as 33. So, minimum health level should be (3 + 6 + 15 + 7) + 1 = 32, right?
- No because if we start with health 4 and follow the path -3 -> 2 -> 4 -> -5 -> 6 -> -2 -> -4, we can definitely reach the princess with lesser initial health.
- Thus, finding the path with minimum sum doesn't work/
Using path with maximum sum(fails)¶

- For the above matrix, the path with maximum sum is -2 -> -8 -> 100 -> 1, which yields sum as 91. So, minimum health level should be (2 + 8) + 1 = 11, right?
- No because if we start with health 7 and follow the path -2 -> -1 -> -3 -> 1, we can definitely reach the princess with lesser initial health.
- Similarly, finding the path with maximum sum doesn't work.
NOTE:
Finding the path with maximum or minimum sum is a greedy approach, which doesn't work for this problem.
How to approach the problem then?¶
Let's start with finding the smallest problem.
Where does smallest problem lie?* (0, 0) ? NO
The smallest problem lies at (M - 1, N - 1), because we need to find the minimum health to finally enter that cell to save the princess.
Now, what should be the minimum health to enter a cell?
Suppose the cell(M - 1, N - 1) has value -4, then to enter the cell needed is: minimum_health + (-4) > 0 => minimum_health + (-4) = 1 => minimum_health = 5
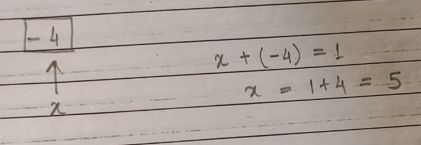
There are two ways to enter the cell:
(1) via TOP (2) via LEFT.
Which one to choose?
We know, to enter the cell with value -4, the minimum health should be 5. Therefore, if we want to enter from top cell with value -2, then x + (-2) = 5; x = 7, where 'x' is minimum health to enter top cell.
Similary, y + (-3) = 5; y = 8.
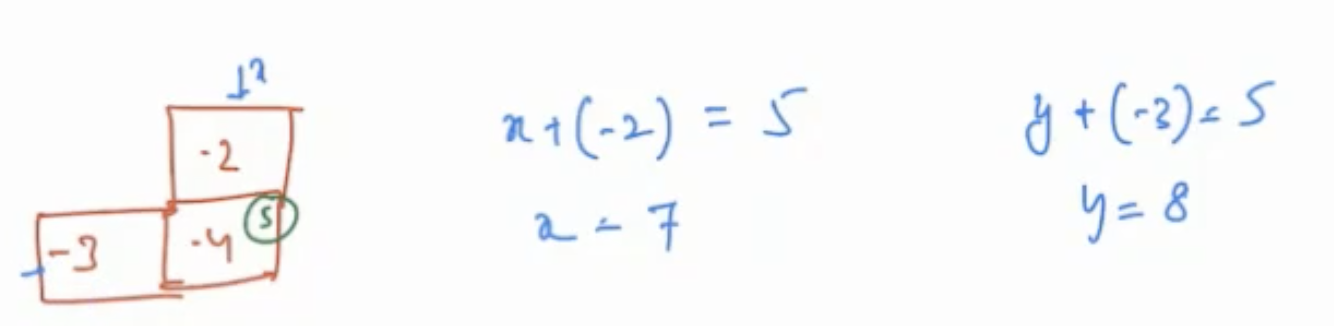
Hence, we should choose minimum of these and enter the cell via top.
What is the minimum health required to enter a cell (i, j) which has two options to move ahead?
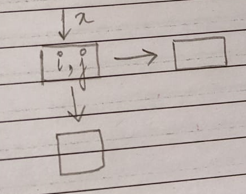
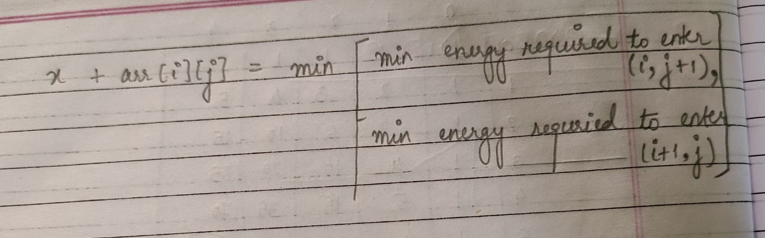
If the minimum health evaluates to negative, we should consider 1 in place of that as with any health <= 0, the prince will die.
Let's fill the matrix using the same approach.
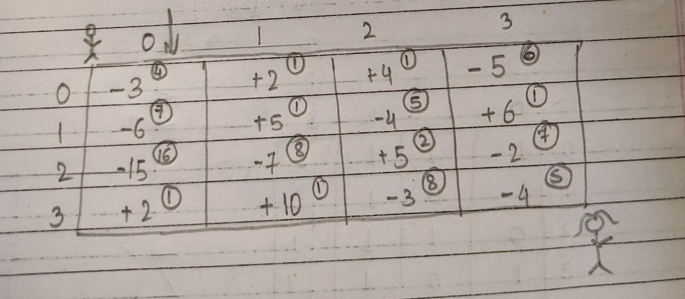
Here, dp[i][j] = min health with which prince should take the entry at (i, j) so that he can save the princess.
Question¶
What is the Time Complexity to find minimum cost path from (0,0) to (r-1, c-1)?
Choices
- O(max(r, c))
- O(c )
- O(r * c)
- O(r + c)
Dungeons and Princess Algorithm and Pseudocode¶
Algorithm¶
arr[i][j] + x = min(dp[i + 1][j], dp[i][j + 1])
x = min(dp[i + 1][j], dp[i][j + 1]) - arr[i][j]
Since x should be > 0
x = max(1, min(dp[i + 1][j], dp[i][j + 1]) - arr[i][j])
Pseudocode:¶
declare dp[N][M];
if (arr[N - 1][M - 1] > 0) {
dp[N - 1][M - 1] = 1;
} else {
dp[N - 1][M - 1] = 1 + abs(arr[N - 1][M - 1]);
}
// Fill the last column and last row
for (i = N - 2; i >= 0; i--) {
for (j = M - 2; j >= 0; j--) {
x = max(1, min(dp[i + 1][j], dp[i][j + 1]) - arr[i][j]);
dp[i][j] = x;
}
}
return dp[0][0];
Complexity¶
Time Complexity: O(N * M)
Space Complexity: O(N * M)
Catalan Numbers¶
The Catalan numbers form a sequence of natural numbers that have numerous applications in combinatorial mathematics. Each number in the sequence is a solution to a variety of counting problems. The Nth Catalan number, denoted as Cn, can be used to determine:
- The number of correct combinations of N pairs of parentheses.
- The number of distinct binary search trees with N nodes, etc.
Here is the sequence,
C0 = 1
C1 = 1
C2 = C0 * C1 + C1 * C0 = 2
C3 = C0 * C2 + C1 * C1 + C2 * C0 = 5
C4 = C0 * C3 + C1 * C2 + C2 * C1 + C3 * C0 = 14
C5 = C0 * C4 + C1 * C3 + C2 * C2 + C3 * C1 + C4 * C0 = 42
Formula¶

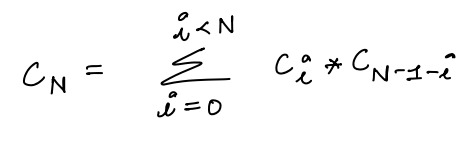
Psuedo Code¶
int C[N + 1];
C[0] = 1;
C[1] = 1;
for (int i = 2; i <= N; i++) {
for (int j = 0; j < i; j++) {
C[i] += C[j] * C[N - 1 - j];
}
}
Complexity¶
Time Complexity: O(N2)
Space Complexity: O(N)
Now, Let's look into a problem, which can be solved by finding the Nth catalan number.
Problem 5 Total Number of Unique BSTs¶
You are given a number N, Count Total number of Unique Binary Search Trees, that can be formed using N distinct numbers.
Example
Input:
N = 3
Output:
5
Explanation:
The Unique binary Search Trees are
30 10 30 10 20
/ \ / \ / \
10 20 20 30 10 30
\ \ / /
20 30 10 20
Question¶
Count Total number of Unique Binary Search Trees, that can be formed using 2 distinct numbers
Choices
- 1
- 2
- 5
- 4
Explanation:
Lets take 2 distinct numbers as [10, 20]
The possible BSTs are
20 10
/ \
10 20
Warning
Please take some time to think about the solution approach on your own before reading further.....
Total Number of Unique BSTs Dryrun¶
Lets take N = 5, the numbers are [10, 20, 30, 40, 50].
Lets keep each number as the root! one by one.
10 as root
10
\
\
\
20, 30, 40, 50
Here we notice that, 20, 30, 40 and 50 can be structured by various sub-roots. So, lets denote by C4.
Also on the right side, there is no elements. So denoting by C0.
10 as root => C0 * C1
20 as root
20
/ \
/ \
/ \
10 30, 40, 50
There are 1 element on the left side and 3 elements on the right side.
20 as root => C1 * C3
30 as root
30
/ \
/ \
/ \
10, 20 40, 50
There are 2 element on the left side and 2 elements on the right side.
30 as root => C2 * C2
40 as root
40
/ \
/ \
/ \
10, 20, 30 50
There are 3 element on the left side and 1 elements on the right side.
40 as root => C0 * C1
50 as root
50
/
/
/
10, 20, 30, 40
There are 4 element on the left side and 1 elements on the right side.
10 as root => C4 * C0
C5 = C0 * C4 + C1 * C3 + C2 * C2 + C3 * C1 + C4 * C0
which is 42.
Solution¶
The Solution for finding the total number of Unique BSTs is the Nth Catalan Number.
Total Number of Unique BSTs Pseudo Code¶
Psuedo Code¶
The pseudo code is same as the Catalan Number Psuedo code.
function findTotalUniqueBSTs(int N) {
int C[N + 1];
C[0] = 1;
C[1] = 1;
for (int i = 2; i <= N; i++) {
for (int j = 0; j < i; j++) {
C[i] += C[j] * C[N - 1 - j];
}
}
return C[N];
}
Complexity¶
Time Complexity: O(N2)
Space Complexity: O(N)
