Advanced DSA: Greedy

---

Introduction on Greedy

The greedy approach deals with maximizing our profit and minimizing our loss.

Example 1:

Suppose we want to buy an iPhone, and the price of an iPhone at Amazon is 1.3 lakhs, the price at Paytm at 1.2 lakhs and the price at Flipkart is 1.25 lakhs. So we will buy an iPhone from Paytm as it has a minimum price. Here we are considering only one factor i.e. the amount of an iphone.

Example 2:

Suppose we want to switch a company and we have three offer letters. The first company is given a 22 LPA offer, the second company is given a 25 LPA, and the third company is given a 28 LPA offer.

So we are going to select 28 LPA offer company. Here we are again considering the money factor, we are not considering the factors:

• Job is remote
• Work culture
• Timings
• Growth

But if 25 LPA company has other facilities better than 28 LPA offer company. 25 LPA company has flexible working hours, provides remote job and good work culture. Then we are going to choose 25 LPA offer company.

If we involve only one factor then selection will become easier and if multiple factors are involved then the decision becomes a bit difficult.

In this lecture, we are going to do questions which involve multiple factors.

---

Problem 1 Flipkart's Challenge in Effective Inventory Management

In the recent expansion into grocery delivery, Flipkart faces a crucial challenge in effective inventory management. Each grocery item on the platform carries its own expiration date and profit margin, represented by arrays A[i] (expiration date for the ith item) and B[i] (profit margin for the ith item). To mitigate potential losses due to expiring items, Flipkart is seeking a strategic solution. The objective is to identify a method to strategically promote certain items, ensuring they are sold before their expiration date, thereby maximizing overall profit. Can you assist Flipkart in developing an innovative approach to optimize their grocery inventory and enhance profitability?

A[i] -> expiration time for ith item

B[i] -> profit gained by ith item

Time starts with T = 0, and it takes 1 unit of time to sell one item and the item can only be sold if T < A[i].

Sell items such that the sum of the profit by items is maximized.

Example

A[] = [3 1 3 2 3]
B[] = [6 5 3 1 9]
index: 0 1 2 3 4

Idea 1 - Pick the highest profit item first

• We will first sell the item with the highest profit.

Initially T = 0

• We have the maximum profit item at index 4, so will sell it and increment T by 1.

T	Item Index	Profit
1	4	9

• Now the item at index 1 can't be sold as A[1] <= T. So we can not sell it.

• Now we will sell the item at 0 index.

T	Item Index	Profit
1	4	9
2	0	6

• Now the item at index 3 can't be sold as A[3] <= T. So we can not sell it.

• Now we will sell the item at 2 index.

T	Item Index	Profit
1	4	9
2	0	6
3	2	3

So we have a total profit: 18.

But we can have a better answer than this answer. Let us try one more combination of selling items.

A[] = [3 1 3 2 3]
B[] = [6 5 3 1 9]
index: 0 1 2 3 4

Initially T = 0

• We have sold the item at index 1 and increment T by 1.

T	Item Index	Profit
1	1	5

• Now we have sold the item at index 4 and again increment T by 1.

T	Item Index	Profit
1	1	5
2	4	9

• Now the item at index 3 can't be sold as A[3] <= T. So we can not sell it.

• Now have sold the item at 0 index.

T	Item Index	Profit
1	1	5
2	4	9
3	0	6

• Now the item at index 2 can't be sold as A[2] <= T. So we can not sell it

So we have a total profit 20.

Here we are getting the total profit greater than the total profit of the previously sold combination of items.

And we can achieve maximum profit 20.

The greedy approach is selecting the path by greedy approach, in greedy we will select one path based on some conditions by assuming that this path will give us the solution.

---

Question

What is the maximum profit we can achieve if we have two items with expiration time in A and profit in B:

A = [1, 2]
B = [3, 1500]

Choices

• 3
• 1500
• 1503
• 0

Explanation

A = [1, 2] B = [3, 1500]

Initially T = 0

• We have selected the item at index 9 and incremented T by 1.

T	Item Index	Profit
1	0	3

• Now we have selected the item at index 1 and again increment T by 1.

T	Item Index	Profit
1	0	3
2	1	1500

So we have a total profit 1503.

---

Solution - Effective Inventory Management

• Pick the highest profit item first approach is not giving us the maximum profit, so it will not work. We have to think of another approach.

Idea: Sell Everything

Our approach is always towards selling all the items so that we can achieve maximum profit. So our approach is to first sell the item with the minimum end time.

For this, we have to sort the expiration time in ascending order.

Example:

A[] = [1, 3, 3, 3, 5, 5, 5, 8]
B[] = [5, 2, 7, 1, 4, 3, 8, 1]

Initially T = 0

• We can sell an item available at index 0, as A[0] = 1, and T < A[0]

T	Item Index	Profit
1	0	5

• We can sell an item available at index 1, as A[1] = 3, and T < A[1]

T	Item Index	Profit
1	0	5
2	1	2

• We can sell a item available at index 2, as A[2] = 3, and T < A[2]

T	Item Index	Profit
1	0	5
2	1	2
3	2	7

• But we can not sell the item available at index 3, as A[3] = 3, and A[3] <= T, here the profit of the item at index 3 is 1, so we ignore it easily as it has very little profit.
• We can sell a item available at index 4, as A[4] = 5, and T < A[4].

T	Item Index	Profit
1	0	5
2	1	2
3	2	7
4	4	4

• We can sell a item available at index 5, as A[5] = 5, and T < A[5].

T	Item Index	Profit
1	0	5
2	1	2
3	2	7
4	4	4
5	5	3

• But we can not sell the item available at index 6, as A[6] = 5, and A[6] <= T. But we can say that we must have to select this item to get the maximum profit as it has the larger profit. But we are rejecting it.
• To select the item available at index 6, we have to remove one of the previously selected items.
• So we want to discard the item with the minimum profit among all the selected items.

T	Item Index	Profit
1	0	5
2	1	2
3	2	7
4	4	4
5	5	3
5	6	8

• We can sell item available at index 7, as A[7] = 8, and T < A[7].

T	Item Index	Profit
1	0	5
2	1	2
3	2	7
4	4	4
5	5	3
5	6	8
6	7	1

So we have a total profit 28.

At any point, if we weren't able to choose a item as T >= A[i] and realize we made a wrong choice before, we will get rid of the item with least profit we previously picked and choose the current one instead.

Approach

The solution to this question is just like the team selection. We have to select the strongest player, if we have any player who is stronger than the player in our team, then we will remove the weaker player from the team and add that player to our team.

Example: Solving using min-heap

	0	1	2	3	4	5	6	7
A[ ]	1	3	3	3	5	5	5	8
B[ ]	5	2	7	1	4	3	8	1

Solution

Initially T = 0 and we have a empty min-heap.

All the items are sorted in the ascending order of expiration time.

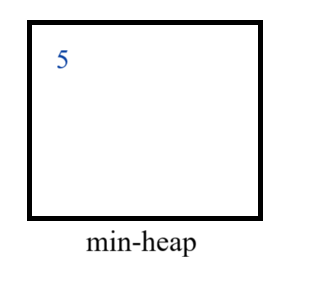
• We can sell a item available at index 0, as A[0] = 1, so here T < A[0], so we will sell the item available at index 0 and add its profit in min-heap.

T = 1

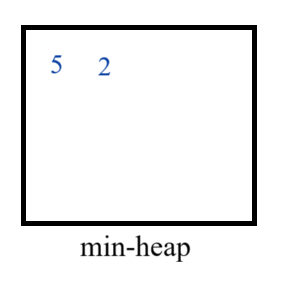
• We can sell a item available at index 1, as A[1] = 3, so here T < A[1], so we will sell the item available at index 1 and add its profit in min-heap.

T = 2

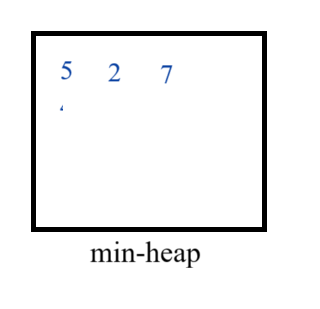
• We can sell a item available at index 2, as A[2] = 3, so here T < A[2], so we will sell the item available at index 2 and add its profit in min-heap.

T = 3

• But we can not sell the item available at index 3, as A[3] = 3, and A[3] <= T. Now we will check if we have taken any incorrect steps in the past.

• We check if we have any items in the heap with profit less than 1. So we have 2 minimum profit in the heap but 2 > 1, so it proves all our past decisions are correct. So we will skip the item available at index 3.

• We can sell a item available at index 4, as A[4] = 5, and T < A[4] and add its profit in min-heap.

T = 4

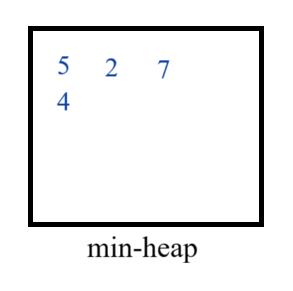
• We can sell a item available at index 5, as A[5] = 5, so here T < A[5] and add its profit in min-heap.

T = 5

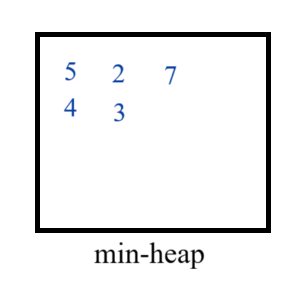
• But we can not sell the item available at index 6, as A[6] = 5, and A[6] <= T. Now we will check if we have made any incorrect decisions in the past.
• We have minimum profit 2 in the heap, so remove it from the heap and add the profit of the item available at index 6 in the heap.

T = 5

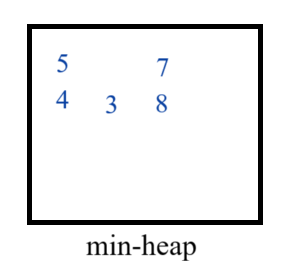
• We can sell a item available at index 7, as A[7] = 8, so here T < A[7], so we will sell the item available at index 7 and add its profit in min-heap.

T = 6

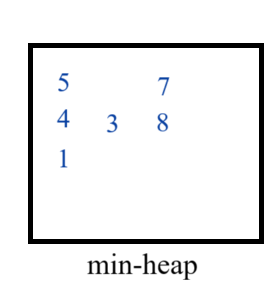
• Now we can find the answer by removing one-by-one elements from the heap and adding them to the answer.

So we have final answer = 1 + 3 + 4 + 5 + 7 + 8 = 28

PseudoCode

1. Sort them in increasing order of time.
2. Minheap heap:
    T = 0
for (i = 0; i < N; i++) {
    if (T < A[i]) {
        heap.insert(B[i])
        T++
    } else {
        if (B[i] <= root of heap) -> ignore {

        }
        else {
            extractMin()
            heap.insert(B[i])
        }
    }
}
3. Remove all elements from the heap and add them to get the answer.

---

Question

What is the time and space complexity of this question?

Choices

• TC: O(N), SC: O(N)
• TC: O(NlogN), SC: O(N)
• TC: O(N²), SC: O(N)
• TC: O(N²) , SC: O(N²)

---

Effective Inventory Management Complexity

Time Complexity

1. Sort them in increasing order of time.-- -> NlogN
2. Minheap heap:
    T = 0
for (i = 0; i < N; i++) {
    -- -> N
    if (T < A[i]) {
        heap.insert(B[i]) -- -> logN
        T++
    } else {
        if (B[i] <= root of heap) -> ignore {

        }
        else {
            extractMin() -- -> logN
            heap.insert(B[i]) -- -> logN
        }
    }
}

3. Remove all elements from the heap and add them to get the answer.

So overall time complexity = O(NlogN) + O(NlogN)

• Time Complexity: O(NlogN)
  
• Space Complexity: O(N)

---

Problem 2 Candy Distribution

There are N students with their marks. The teacher has to give them candies such that

a) Every student should have at least one candy b) Students with more marks than any of his/her neighbours have more candies than them.

Find minimum candies to distribute.

Example

Input: [1, 5, 2, 1]

Explanation:

First we will give 1 candy to all students.

index	0	1	2	3
marks	1	5	2	1
candy	1	1	1	1

Index 1 student has marks greater than their neighbours. So it must have candies greater than his neighbors.

index	0	1	2	3
marks	1	5	2	1
candy	1	1 2	1	1

Index 2 student has marks greater than its right neighbour. So it must have candies greater than his right neighbour.

index	0	1	2	3
marks	1	5	2	1
candy	1	1 2	1 2	1

Now index 1 student again has marks greater than both neighbors but its candies are not greater than its right neighbor's candies. So it must have candies greater than his both neighbors.

index	0	1	2	3
marks	1	5	2	1
candy	1	1 2 3	1 2	1

Now all the conditions of the question are satisfied, so total 7 candies are required to be distributed among students.

Output: 7

---

Question

What is the minimum number of candies teacher has to use if the marks are: [4, 4, 4, 4, 4]

Choices

• 1
• 5
• 10
• 20

Explanation

[4, 4, 4, 4, 4]

First, we will give 1 candy to all students. |index|0|1|2|3|4| |-|-|-|-|-|-| |marks|4|4|4|4|4| |candy|1|1|1|1|1|

Now any student does not have marks greater than its neighbors. So our candy distribution is perfect.

So total 5 candies are required.

---

Candy Distribution Example

Example

Input: [8, 10, 6, 2]

First, we will give 1 candy to all students. |index|0|1|2|3| |-|-|-|-|-| |marks|8|10|6|2| |candy|1|1|1|1|

• Now student at index 2 has marks greater than its right neighbor, so it receive 2 candies.

index	0	1	2	3
marks	8	10	6	2
candy	1	1	1 2	1

• Student at index 1 has marks greater than both neighbours, so it must candies greater than both neighbours. So it receives 3 candies.

index	0	1	2	3
marks	8	10	6	2
candy	1	1 3	1 2	1

So total 7 candies are required.

Output: 7

---

Question

What is the minimum number of candies the teacher has to use if the marks are: [1, 6, 3, 1, 10, 12, 20, 5, 2]

Choices

• 15
• 19
• 21
• 20

Explanation

[1, 6, 3, 1, 10, 12, 20, 5, 2]

First, we will give 1 candy to all students. | index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |:-----:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:| | marks | 1 | 6 | 3 | 1 | 10 | 12 | 20 | 5 | 2 | | candy | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |

First, let us consider the left nighbor of all the indexes.

• Now a student at index 1 has marks greater than its left neighbour, so it should receive at least 2 candies.

index	0	1	2	3	4	5	6	7	8
marks	1	6	3	1	10	12	20	5	2
candy	1	1 2	1	1	1	1	1	1	1

• Now student at index 2, and 3 does not have marks greater than their left neighbour.

• Student at index 4 has marks greater than its left neighbour, so it should receive at least 2 candies.

index	0	1	2	3	4	5	6	7	8
marks	1	6	3	1	10	12	20	5	2
candy	1	1 2	1	1	1 2	1	1	1	1

• Student at index 5 has marks greater than its left neighbour, so it should receive at least 3 candies.

index	0	1	2	3	4	5	6	7	8
marks	1	6	3	1	10	12	20	5	2
candy	1	1 2	1	1	1 2	1 3	1	1	1

• Student at index 6 has marks greater than its left neighbour, so it should receive at least 4 candies.

index	0	1	2	3	4	5	6	7	8
marks	1	6	3	1	10	12	20	5	2
candy	1	1 2	1	1	1 2	1 3	1 4	1	1

• Student at index 7 and index 8 does not have marks greater than their left neighbour.

Now let us consider the right neighbour.

• Student at index 7 has marks greater than its right neighbour, so it should receive at least 2 candies.

index	0	1	2	3	4	5	6	7	8
marks	1	6	3	1	10	12	20	5	2
candy	1	1 2	1	1	1 2	1 3	1 4	1 2	1

• Student at index 6 has marks greater than its right neighbour, so it should receive at least 3 candies but it has 4 candies already which is greater than its right neighbour candies, so it is fine.

• Student at index 5, 4 and 3 do not have marks greater than their right neighbour.

• Student at index 2 has marks greater than its right neighbour. So it receives at least 2 candies.

index	0	1	2	3	4	5	6	7	8
marks	1	6	3	1	10	12	20	5	2
candy	1	1 2	1 2	1	1 2	1 3	1 4	1 2	1

• Student at index 1 has marks greater than its right neighbour. So it receives at least 3 candies.

index	0	1	2	3	4	5	6	7	8
marks	1	6	3	1	10	12	20	5	2
candy	1	1 2 3	1 2	1	1 2	1 3	1 4	1 2	1

• Student at index 0 does not have marks greater than its right neighbour.

So a total 19 candies are required.

Output: 19

---

Candy Distribution - Solution

Warning

Please take some time to think about the solution approach on your own before reading further.....

Step 1:

Assign 1 candy to all the students.

Step 2:

For all the values of i, consider its left neighbour, if(A[i] > A[i - 1]) then C[i] > C[i - 1], means candy of ith index should be greater than (i-1)th index candy, so we will follow the greedy approach as we want to distribute a minimum number of candies, so we do C[i] = C[i - 1] + 1

if(A[i] > A[i - 1]){
    C[i] = C[i - 1] + 1
}

Step 3:

For all the values of i, consider its right neighbour, if(A[i] > A[i+1]) then C[i] > C[i + 1], means candy of ith index should be greater than (i+1)th index candy, so first we check it has candies greater than his right neighbour or not if not then we will follow the greedy approach as we want to distribute a minimum number of candies, then we do C[i] = C[i + 1] + 1

if(A[i] > A[i + 1]){
    if(C[i] < C[i + 1] + 1)
        C[i] = C[i + 1] + 1
}

PsuedoCode

int C[N];
for all i, C[i] = 1
for (i = 1; i < N; i++) {
    if (arr[i] > arr[i - 1]) {
        C[i] = C[i - 1] + 1
    }
}
for (i = N - 2; i >= 0; i--) {
    if (arr[i] > arr[i + 1] && C[i] < C[i + 1] + 1) {
        C[i] = C[i + 1] + 1
    }
}

ans = sum of all values in C[]

Complexity

• Time Complexity: O(N)
  
• Space Complexity: O(N)

---

Problem 3 Maximum jobs

Given N jobs with their start and end times. Find the maximum number of jobs that can be completed if only one job can be done at a time.

Example

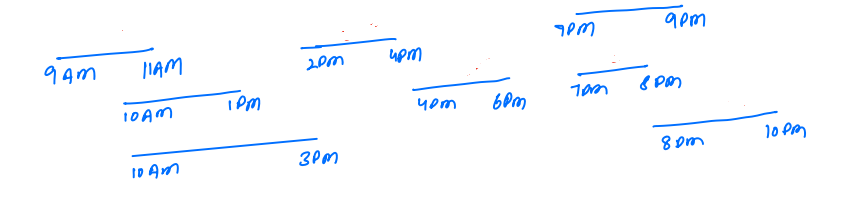
Answer: 5

We will select the jobs that are not overlapping:

• We select job 9 am - 11 am, then we can not select 10 am - 1 pm and 10 am - 2 pm
• Then we select jobs 3 pm - 4 pm and 4 pm - 6 pm
• Then we select job 4 pm - 8 pm and 8 pm - 10 pm but we do not select job 7 pm - 9 pm

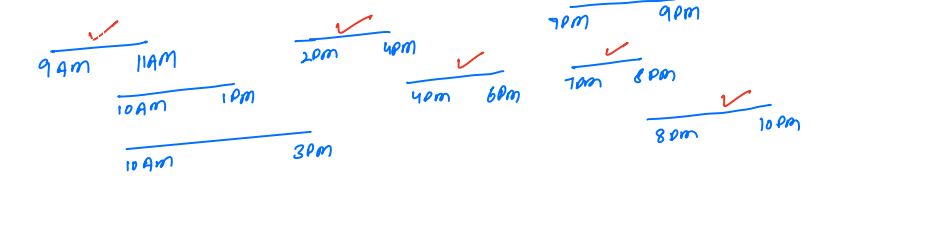
Approach

We have to select the job in such a way that the start time of a currently selected job is greater than or equal to the end time of the previous job.

S[i] >= E[i - 1]

---

Question

What is the maximum number of jobs one person can do if only one job at a time is allowed, the start times and end times of jobs are:

S = [1, 5, 8, 7, 12, 13]
E = [2, 10, 10, 11, 20, 19]

Choices

• 2
• 3
• 4
• 5

Explanation

S = [1, 5, 8, 7, 12, 13]
E = [2, 10, 10, 11, 20, 19]

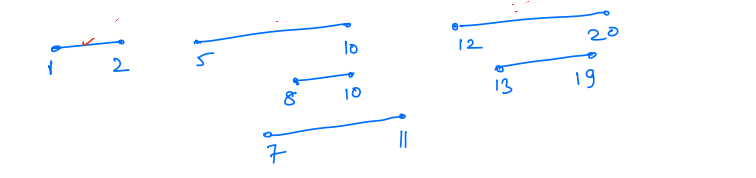
We will pick jobs 1 - 2, 5 - 10 and 12 - 20. So we can pick total three jobs.

---

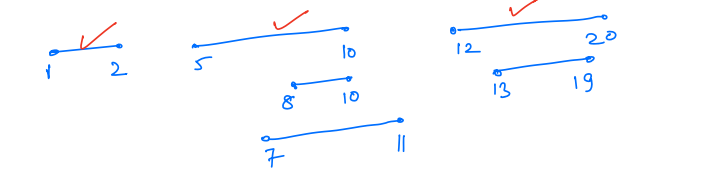
Maximum jobs - Solution

The first idea towards a solution is to first pick a job with minimum duration.

Idea 1 - Greedy based on duration

Pick the job in the ascending order of the minimum duration. Let us take an example:

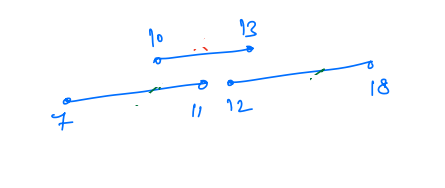
In this case, if we select the minimum duration job first, then we will select the job 10 - 13, then we can not select any other job because both overlap with it.

But if we have not selected 10 - 13, then we can select both other jobs, which means we can select two jobs.

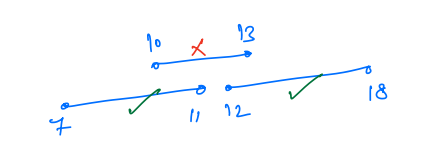
So selecting a job in the ascending order of the duration will not always give us the maximum number of jobs.

Idea 2 - Greedy based on start time

Pick the job in the ascending order of the start time. Let us take an example:

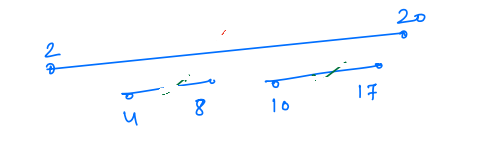
In this case, if we select the minimum start time job first, then we will select the job 2 - 20, then we can not select any other job because both overlap with it.

But if we have not selected 2 - 20, then we can select both other jobs, which means we can select two jobs.

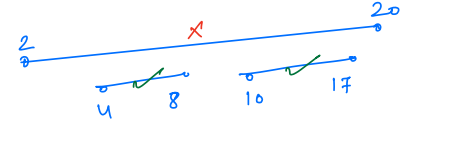
So selecting a job in the ascending order of the start time will not always give us the maximum number of jobs.

Observation

We have to take a combination of the above approaches means we have to start early with the minimum duration job.

start early + minimum duration

A combination of both is nothing but simply means ending early.

start early + minimum duration = end early

Solution

We have to be greedy based on the end time, so we have to select jobs in the ascending order of end times.

Example:

S = [1, 5, 8, 7, 12, 13]
E = [2, 10, 10, 11, 20, 19]

Sort these jobs based on the end time.

S = [1, 5, 8, 7, 13, 12]
E = [2, 10, 10, 11, 19, 20]

Initially ans = 0.

Index	0	1	2	3	4	5
Start time	1	5	8	7	13	12
end time	2	10	10	11	19	20

• We will start with the first job, which has an end time 2 but now the start time of any next job must be greater than the end time of this job.

So we need to keep track of the last end time.

Till now lastEndTime = 2
ans+=1, ans = 1

• Now the job at index 1 has start time = 5, lastEndTime <= start time, so can select this job and lastEndTime will be updated to the end time of the current job and the answer is incremented by 1.
  lastEndTime = 10
  ans+=1, ans = 2
• Now the job at index 2 has start time = 8, lastEndTime > start time, so we can not select this job.
• Now the job at index 3 has start time = 7, lastEndTime > start time, so we can not select this job.
• Now the job at index 4 has start time = 13, lastEndTime <= start time, so can select this job and lastEndTime will be updated to the end time of the current job and the answer is incremented by 1.
  lastEndTime = 19
  ans+=1, ans = 3
• Now the job at index 5 has start time = 20, lastEndTime > start time, so we can not select this job.

Answer: 3

PseudoCode

1. Sort on the basis of end-time
2. ans = 1, lastEndTime = E[0]
   for( i = 1 ; i < N ; i++){
       if(S[i] >= lastEndTime){
           ans++;
           lastEndTime = E[i];
       }
   }
3. return ans;

Complexity

• Time Complexity: O(NlogN)
  
• Space Complexity: O(N)

---