Hashmap Implementation¶

Check if given element exists in Q queries¶

Given an array of size N and Q queries. In each query, an element is given. We have to check whether that element exists or not in the given array.

Example

A [ ] = {2, 4, 11, 15 , 6, 8, 14, 9}

4 Queries
K = 4 (return true)
K = 10 (return false)
K = 17 (return false)
K = 14 (return true)

Warning

Please take some time to think about the solution approach on your own before reading further.....

Brute Force Approach¶

For every query, loop through the given array to check the presence.

Time Complexity - O(N * Q)
Space Complexity - O(1)

Observation¶

We can create an array to mark the presence of an element against that particular index.

A [ ] = {2, 4, 11, 15 , 6, 8, 14, 9}

For example we can mark presence of
2 at index 2
4 at index 4 and so on....

To execute that, we'll need to have indices till 15(max of Array).
The array size needed is 16.

Let's call that array as - DAT (Direct Access Table)
int dat[16] = {0}; //initally assuming an element is not present

0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0

Let's mark the presence.

for(int i = 0; i < N; i++) {
    dat[A[i]] = 1;
}

Below is how that array looks like -

0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
0	0	1	0	1	0	1	0	1	1	0	1	0	0	1	1

Advantage of using DAT¶

Time Complexity of Insertion - O(1)
Time Complexity of Deletion - O(1)
Time Complexity of Search - O(1)

Issues with such a representation¶

1. Wastage of Space

Say array is A[] = {23, 60, 37, 90}; now just to store presence of 4 elements, we'll have to construct an array of size 91.

2. Inability to create big Arrays

If values in array are as big as \(10^{15}\), then we will not be able to create this big array. At max array size possible is 10⁶(around)

3. Storing values other than positive Integers

We'll have to make some adjustments to store negative numbers or characters. (It'll be possible but needs some work-around)

Overcome Issues while retaining Advantages¶

Let's say we have restriction of creating only array of size 10.

Given Array -
A [ ] = {21, 42, 37, 45 , 99, 30}

How can we do so ?

In array of size 10, we'll have indices from 0 to 9. How can we map all the values within this range ?

Basically, we can take a mod with 10.

21 % 10 = 1 (presence of 21 can be marked at index 1)

42 % 10 = 2 (presence of 42 can be marked at index 2)

37 % 10 = 7 (presence of 37 can be marked at index 7)

45 % 10 = 5 (presence of 45 can be marked at index 5)

99 % 10 = 9 (presence of 99 can be marked at index 9)

30 % 10 = 0 (presence of 30 can be marked at index 0)

0	1	2	3	4	5	6	7	8	9
30	21	42	0	0	45	0	37	0	99

What Have We Done ?¶

We have basically done Hashing. Hashing is a process where we pass our data through the Hash Funtion which gives us the hash value(index) to map our data to.
In this case, the hash function used is MOD. This is the simplest hash function. Usually, more complex hash functions are used.
The DAT that we created is known as Hash Table in terms of Hashing.

Issue with Hashing ?¶

COLLISION!

Say given array is as follows -

A [ ] = {21, 42, 37, 45, 77, 99, 31}

Here, 21 & 31 will map to the same index => 1 37 & 77 map to same index => 7

Can we completely avoid collision ?

Not Really!

No matter how good a hash function is, we can't avoid collision!

Why ?

We are trying to map big values to a smaller range, collisions are bound to happen.

Moreover, this can be explained using Pigeon Hole Principle!

Example -

Say we have 11 pigeons and we have only 8 holes to keep them. Now, provided holes are less, atleast 2 pigeons need to fit in a single hole.

But, we can find some resolutions to collision.

Collision Resolution Techniques¶

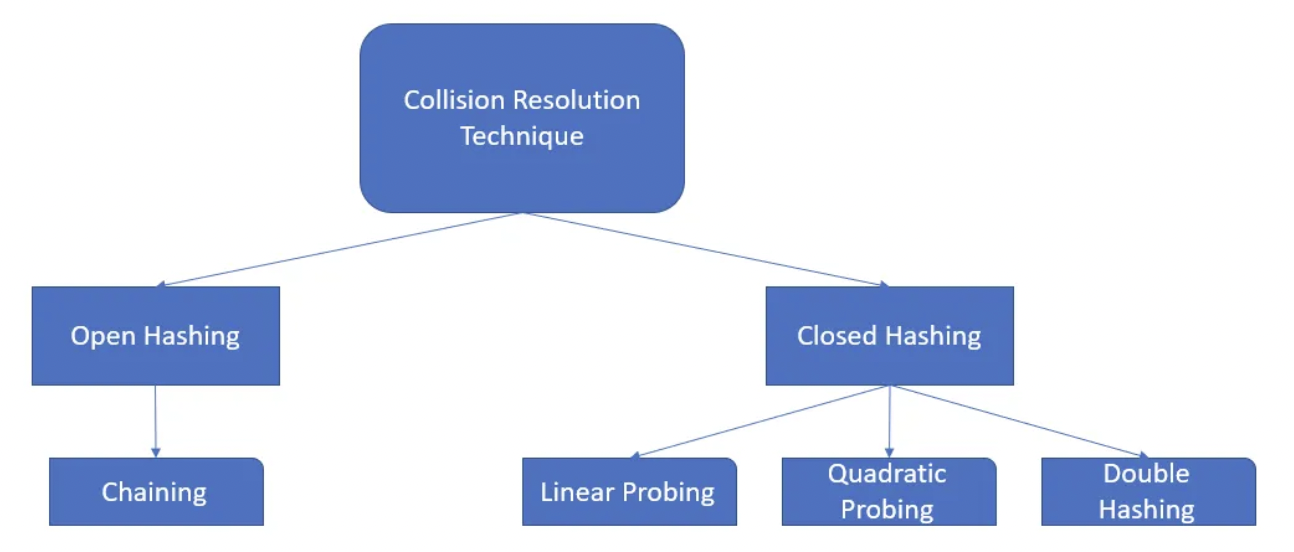
From Interview Perspective, Open Hashing is Important hence, we'll dive into that.

Chaining¶

Let's take the above problem where collision happened!

A [ ] = {21, 42, 37, 45, 77, 99, 31}

Here, 21 & 31 will map to the same index => 1 37 & 77 map to same index => 7

How can we resolve Collision here?

We can somehow store both 21 & 31 at the same index.

Basically we can have a linked list at every index.
i.e, Array of Linked List

Every index shall have head node of Linked List.

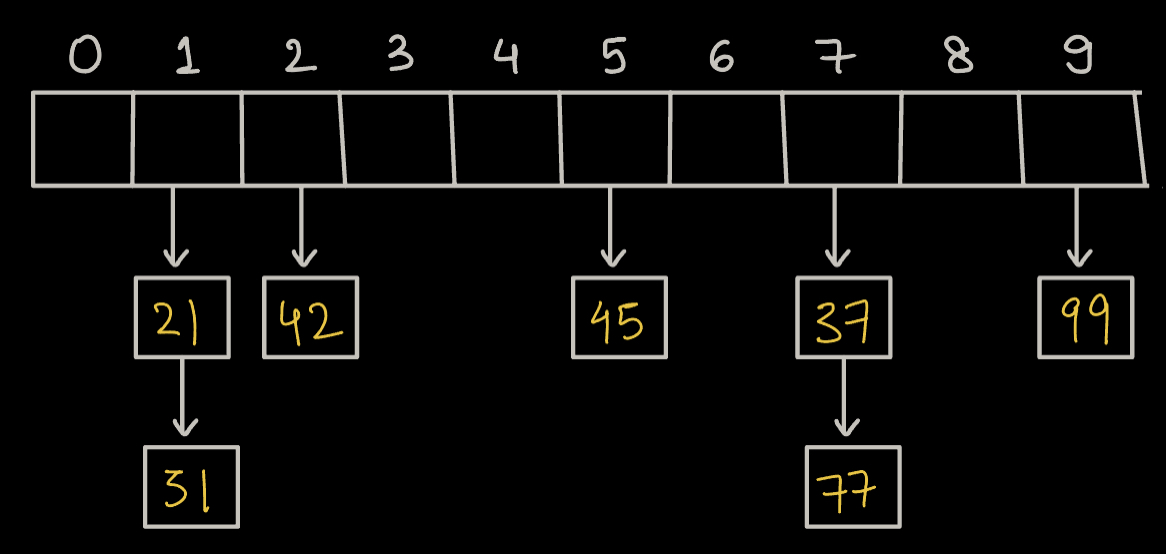
The above method is known as Chaining.

Chaining is a technique used in data structures, particularly hash tables, to resolve collisions. When multiple items hash to the same index, chaining stores them in a linked list or another data structure at that index.

What will be the Time Complexity of Insertion ?

First we will pass the given element to Hash Function, which will return an index. Now, we will simply add that element to the Linked List at that index.
If we insert at tail => O(N)
If we insert at head => O(1)

Since order of Insertion doesn't matter to us, so we can simply insert at head.

What will be the Time Complexity of Deletion and Searching ?

Time Complexity on average is always less than \(\lambda\). \(\lambda\) is known as lamda.
Time Complexity in worst case is still O(N)

What is lamda¶

There is a lamba(\(\lambda\)) function which is nothing but a ratio of (number of elements inserted / size of the array).

Example:

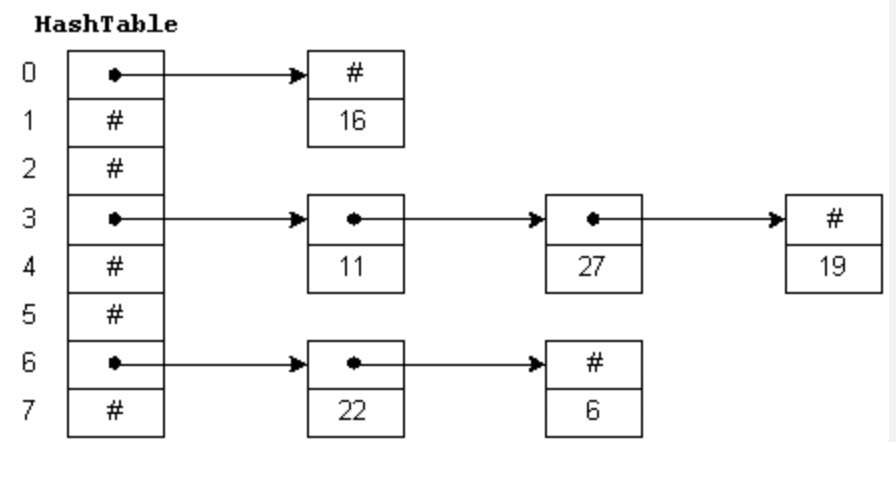
Table size(Array size) = 8
Inserted Elements = 6

\(\lambda\) = \(\frac{6}{8}\) = 0.75

Let's assume the predefined threshold is 0.7. The load factor is exceeding this value, so we will need to rehash the table.

Rehashing:

Create a new hash table with double the size of the original hash table. In this case, the new size will be
8×2=16
Redistribute the existing elements to their new positions in the larger hash table using a new hash function.
The load factor is now recalculated for the new hash table:
\(\lambda\) = \(\frac{6}{16} = 0.375\) (within the threshold of 0.7)

Code Implementation¶

Declaring the HashMap Class¶

Let's go through the code implementation of a hashmap:

The HashMap class is defined with generic types K and V for keys and values.
The inner class HMNode represents a node containing a key-value pair.
buckets is an array of ArrayLists to store key-value pairs.
size keeps track of the number of key-value pairs in the hashmap.
The initbuckets() method initializes the array of buckets with a default size of 4.

import java.util.ArrayList;

class HashMap < K, V > {

        private class HMNode {
            K key;
            V value;

            public HMNode(K key, V value) {
                this.key = key;
                this.value = value;
            }
        }

        private ArrayList < HMNode > [] buckets;
        private int size; // number of key-value pairs

        public HashMap() {
            initbuckets();
            size = 0;
        }

        private void initbuckets() {
            buckets = new ArrayList[4];
            for (int i = 0; i < 4; i++) {
                buckets[i] = new ArrayList < > ();
            }
        }

Put Method¶

The put method adds a key-value pair to the hashmap.
It calculates the bucket index (bi) using the hash method and finds the data index within the bucket using getIndexWithinBucket.
If the key is found in the bucket, it updates the value. Otherwise, it inserts a new node.
After inserting, it checks the load factor (lambda) and triggers rehashing if the load factor exceeds 2.0.

    public void put(K key, V value) {
        int bi = hash(key);
        int di = getIndexWithinBucket(key, bi);

        if (di != -1) {
            // Key found, update the value
            buckets[bi].get(di).value = value;
        } else {
            // Key not found, insert new key-value pair
            HMNode newNode = new HMNode(key, value);
            buckets[bi].add(newNode);
            size++;

            // Check for rehashing
            double lambda = size * 1.0 / buckets.length;
            if (lambda > 2.0) {
                rehash();
            }
        }
    }

Hash Method¶

The hash method calculates the bucket index using the hash code of the key and takes the modulus to ensure it stays within the array size.

    private int hash(K key) {
      int hc = key.hashCode();
      int bi = Math.abs(hc) % buckets.length;
      return bi;
  }

Get Index within Bucket¶

The getIndexWithinBucket method searches for the data index (di) of a key within a specific bucket. It returns -1 if the key is not found

    private int getIndexWithinBucket(K key, int bi) {
        int di = 0;
        for (HMNode node: buckets[bi]) {
            if (node.key.equals(key)) {
                return di; // Key found
            }
            di++;
        }
        return -1; // Key not found
    }

Rehash Method¶

The rehash method is called when the load factor exceeds 2.0.
It creates a new array of buckets, initializes the size to 0, and iterates through the old buckets, reinserting each key-value pair into the new array.

    private void rehash() {
        ArrayList < HMNode > [] oldBuckets = buckets;
        initbuckets();
        size = 0;

        for (ArrayList < HMNode > bucket: oldBuckets) {
            for (HMNode node: bucket) {
                put(node.key, node.value);
            }
        }
    }

Get Method¶

The get method retrieves the value associated with a given key. It calculates the bucket index and searches within the bucket to find the key.

    public V get(K key) {
        int bi = hash(key);
        int di = getIndexWithinBucket(key, bi);

        if (di != -1) {
            return buckets[bi].get(di).value;
        } else {
            return null;
        }
    }

Contains Key Method¶

The containsKey method checks if a given key exists in the hashmap by calculating the bucket index and checking the data index within the bucket.

    public boolean containsKey(K key) {
        int bi = hash(key);
        int di = getIndexWithinBucket(key, bi);

        return di != -1;
    }

Remove Method¶

The remove method removes a key-value pair from the hashmap. If the key is found, it returns the value; otherwise, it returns null

    public V remove(K key) {
        int bi = hash(key);
        int di = getIndexWithinBucket(key, bi);

        if (di != -1) {
            // Key found, remove and return value
            size--;
            return buckets[bi].remove(di).value;
        } else {
            return null; // Key not found
        }
    }

Size Method¶

The size method returns the total number of key-value pairs in the hashmap.

    public int size() {
        return size;
    }

Key Set Method¶

The keyset method returns an ArrayList containing all the keys in the hashmap by iterating through the buckets and nodes.

    public ArrayList < K > keyset() {
        ArrayList < K > keys = new ArrayList < > ();
        for (ArrayList < HMNode > bucket: buckets) {
            for (HMNode node: bucket) {
                keys.add(node.key);
            }
        }
        return keys;
    }
    }

Question¶

What is the time complexity of the brute-force approach for checking the existence of an element in the array for Q queries?

Choices

O(N)
O(Q)
O(N * Q)
O(1)

Question¶

What advantage does the Direct Access Table (DAT) provide in terms of time complexity for insertion, deletion, and search operations?

Choices

O(1) for all operations
O(N) for all operations
O(1) for insertion and deletion, O(N) for search
O(N) for insertion and deletion, O(1) for search

Question¶

What is the purpose of the load factor (lambda) in a hashmap?

Choices

It represents the number of elements in the hashmap.
It is used to calculate the hash code of a key.
It determines when to trigger rehashing.
It controls the size of the hashmap.

Question¶

What does the rehashing process involve in a hashmap?

Choices

Reducing the size of the hashmap
Creating a new hash table with double the size and redistributing elements
Deleting all elements from the hashmap
Removing collision resolution techniques