Hashing Problems

---

Problem 1 Pair Sum K

Given arr[N] and K, check if there exists a pair(i, j) such that,

arr[i] + arr[j] == K && i != j

Example

Let's say we have an array of 9 elements and K, where K is our target sum,

Index	0	1	2	3	4	5	6	7	8
Array	8	9	1	-2	4	5	11	-6	4

K = 6: arr[2] + arr[5] : such a pair exists
K = 22: does not exist
K = 8: arr[4] + arr[8]: such a pair exists

Hence if K = 6 or 8 the answer is true, for K = 22, it will be false.

---

Question

Check if there exists a pair(i, j) such that, arr[i] + arr[j] == K && i != j in the given array A = [3, 5, 1, 2, 1, 2] and K = 7.

Choices

• true
• false

Question

Check if there exists a pair(i, j) such that, arr[i] + arr[j] == K && i != j in the given array A = [3, 5, 1, 2, 1, 2] and K = 10.

Choices

• true
• false

---

Warning

Please take some time to think about the bruteforce approach on your own before reading further.....

Problem 1 Brute Force

Idea 1:

Iterate on all pairs(i, j) check if their sum == k

Example 2:

Take another example of arr[5]

Index	0	1	2	3	4
arr[5]	3	2	6	8	4

We can have following cases of pairs from an array of size 5

• Here, since we are not allowed to consider pairs where i == j these diagonal elements (marked in red) will not be considered.
• Now, as you can see the upper (blue) and lower (yellow) triangles represent the same pairs (order of pair doesn't matter here) our program would work with either one of these triangular parts.

Now, considering upper triangle -

Observation:

i	j loops from [i...(N - 1)]
0	[0..N-1]
1	[1..N-1]
2	[2..N-1]
3	[3..N-1]
4	-

Here for every index of i, j loops from i to N - 1

For an arr[i], the target will be K-arr[i]

Pseudocode:

boolean checkPair(int arr[], int K) {

    int N = arr.length
    for (int i = 0; i < N; i++) {
        //target: K-arr[i]
        for (int j = i; j < N; j++) {
            if (arr[i] == K - arr[i]) {
                return true;
            }
        }
    }
    return false;
}

Complexity

Time Complexity: O(N^2)

Space Complexity: O(1)

---

Problem 1 Optimization with HashSet(Doesn't Work)

• We can insert all elements in the set initially.
• Now, iterate over every arr[i] and check if K-arr[i] is present in the set. If yes, return tue, else false.

---

ISSUE: (Edge Case)

• For even K value, say arr[i] is K/2 and only one occurrence of it is present.
• Eg: A[] = {8, 9, 2, -1, 4, 5, 11, -6, 4}; K=4, we will end up considering 2(present at index 2) two times.

We can see the above logic isn't working

Resolution:

We need not insert all elements into set at once. Rather only insert from [0, i - 1].

---

Problem 1 Optimization with HashSet(Works)

At ith index: Hashset should contain all the elements:[0...i - 1]

Let's take an example,

• Initially set is empty.
• For every element at ith index, search for target (arr[i] - K) in set.
• If found, it means it must have been previously inserted. If not, we'll insert arr[i], because in future if we'll find a pair, we'll be able to get the current element.

Let's take another example,

Pseudocode:

boolean targetSum(int arr[], int K) {
    int N = arr.length;
    Hashset < int > bs;

    for (int i = 0; i < N; i++) {
        //target = K - arr[i]
        if (bs.contains(K - arr[i])) {
            return true;
        } else {
            bs.add(arr[i]);
        }
    }
    return false;
}

---

Question

Count pairs(i, j) such that, arr[i] + arr[j] == K && i != j in the given array. A = [3, 5, 1, 2, 1, 2] and K = 3.

Choices

• 1
• 2
• 3
• 4

In the given array A = [3, 5, 1, 2, 1, 2], pairs with sum = 3 are:

Pairs
{2, 3}
{2, 5}
{3, 4}

---

Problem 2 Count no. of pairs with sum K

Given an arr[n], count number of pairs such that

arr[i] + arr[j] = K && i != j

Example

Provided we have an arr[8] and K = 10, we have

Index	0	1	2	3	4	5	6	7
arr[8]	2	5	2	5	8	5	2	8

Pairs:

Pairs: 9
{0, 4}
{0, 7}
{1, 5}
{1, 3}
{2, 4}
{2, 7}
{3, 5}
{4, 6}
{6, 7}

Here (i, j) and (j, i) considered as same.

Warning

Please take some time to think about the optimised approach on your own before reading further.....

Optimised Approach(Same as in previous question)

• Similar to our previous problem, we'll be searching for our target.
• This time we also need to consider the frequency of how many times a particular element appeared, so we shall be maintianing a map.

Pseudocode:

int countTargetSum(int arr[], int K) {
    int N = arr.length;
    Hashmap < int, int > hm;

    int c = 0;

    for (int i = 0; i < n; i++) {
        //target = K-arr[i]
        if (hm.contains(K - arr[i])) {
            c = c + hm[K - arr[i]] //freq of target = pairs
        }

        //insert arr[i]
        if (hm.contains(arr[i])) {
            hm[arr[i]]++;
        } else {
            hm.put(arr[i], 1);
        }
    }
    return c;
}

Complexity

Time Complexity: O(N)

Space Complexity: O(N)

---

Problem 3 Subarray with Sum K

Given an array arr[n] check if there exists a subarray with sum = K

Example:

We have the following array

Index	0	1	2	3	4	5	6	7	8
arr[7]	2	3	9	-4	1	5	6	2	5

Possible subarrays for the following values of K are,

• k = 11: {2 3 9 -4 1}, {5, 6}
• k = 10: {2 3 9 -4}
• k = 15: {-4, 1, 5, 6, 2, 5}

---

Question

Check if there exist a subarray with sum = 110 in the given array?
A = [ 5, 10, 20, 100, 105 ]

Choices

• No
• YES

---

Approach

To get subarray sum for any subarray in constant time, we can create a prefix sum array.

Now, a subarray sum PF[i] - PF[j] should be equal to K

OR

a - b = K

We can fix a and get the corresponding pair for it, given by a - K

We can create a HashSet at the time of traversal simultaneously
Here, instead of creating prefix sum initially, we are calculating it while iterating through the array.

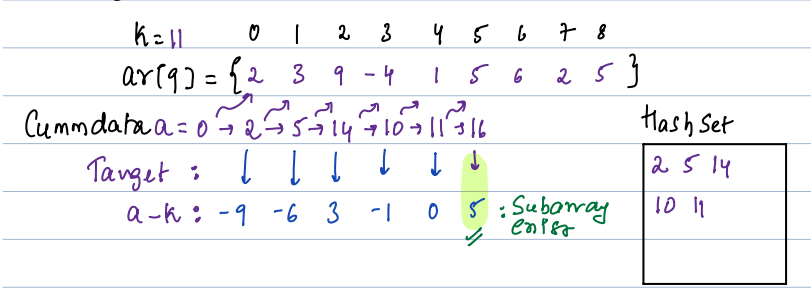
Edge case:

If subarray from index 0 has sum = K.
Say, K = 10
a = 10, b = 10-10=0, now 0 won't be present in the array.
Please take below example:

To resolve this, take 0 in the set initially.

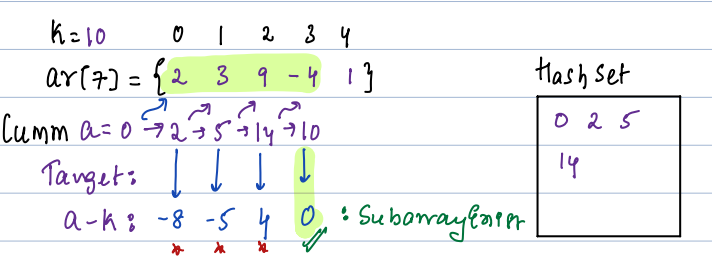
Pseudocode:

boolean targetSubarray(int arr[], int K) {
    int N = arr.length;
    long a = 0;

    //cumulative sum, long -> to avoid overflow
    HashSet < long > hs;
    hs.add(0);
    for (int i = 0; i < N; i++) {
        a = a + arr[i];

        //cumulative sum = target = a - k
        if (hs.contains(a - K)) {
            //subarray exists
            return true;
        } else {
            hs.add(a);
        }
    }
    return false;
}

Complexity

Time Complexity: O(N)

Space Complexity: O(N)

---

Problem 4 Distinct elements in every window of size K

Given an array of integers and a number, K. Find the count of distinct elements in every window of size K in the array.

Example

// Input:
Array = [1, 2, 1, 3, 4, 2, 3]
K = 4

// Output:
[3, 4, 4, 3]

• In the first window [1, 2, 1, 3], there are 3 distinct elements: 1, 2, and 3.
• In the second window [2, 1, 3, 4], there are 4 distinct elements: 2, 1, 3, and 4.
• In the third window [1, 3, 4, 2], there are again 4 distinct elements: 1, 3, 4, and 2.
• In the fourth window [3, 4, 2, 3], there are 3 distinct elements: 3, 4, and 2.

Warning

Please take some time to think about the solution approach on your own before reading further.....

Approach - Using HashSet

• The code iterates through each possible window of size K in the given array.
• For each window, a temporary HashSet (distinctSet) is created to store the distinct elements within that window.
• Within the inner loop, the code adds each element of the window to the HashSet.
• After processing the entire window, the size of the HashSet is calculated using distinctSet.size(), which represents the count of distinct elements.
• The count is then added to the result list.
• This process is repeated for all possible windows in the array.
• The result list contains the count of distinct elements in each window

Pseudocode

//Pseudo code for 'countDistinctElements' function
function countDistinctElements(arr, k):
    result = empty list

    for i = 0 to length of arr - k:
        distinctSet = empty set

        for j = i to i + k - 1:
            add arr[j] to distinctSet

        add size of distinctSet to result

    return result

Complexity

Time Complexity: O((N-K+1) * K)

Considering the values of K as N/2, 1, and N.

When K = N/2:

If K is about half of N, then the expression simplifies to O((N/2 + 1) * N/2), which further simplifies to O((N^2 + N) / 4). In this case, the primary factor is N^2, leading to a time complexity of approximately O(N^2).

When K = 1:

When K is set to 1, the expression becomes O((N - 1 + 1) * 1), which straightforwardly simplifies to O(N). It's important to note that this doesn't align with the original statement of the time complexity being O(N^2).

When K = N:

If K is equal to N, then the expression becomes O((N - N + 1) * N), which further simplifies to O(N^2).

Space Complexity: O(K)

---

Problem 4 Sliding Window - Map

Sliding Window suggests to insert all elements of the first window in the set. Now slide the window, throw the prev element out and insert new adjacent element in the set.

But we can't use Set here, since it is possible that the element just thrown out may be present in the current window.

We will also need to maintain the frequency of elements, hence we will use Hashmap.

• Maintain a HashMap to track the frequency of elements within the current subarray.
• Initially, the algorithm populates the HashMap with the elements of the first subarray, counting distinct elements.
• Then, as the window slides one step at a time:
  • The algorithm updates the HashMap by updating frequency of the element leaving the window and increasing frequency of the new element entering the window.
• The distinct element count for each subarray is determined by the size of the HashMap.

Pseudocode

void subfreq(int ar[], int k) {
  int N = ar.length;

  HashMap < int, int > hm;

  // Step 1: Insert 1st subarray [0, k-1]
  for (int i = 0; i < k; i++) {
    //Increase frequecy by 1
    if (hm.contains(ar[i])) {
      int val = hm.get(ar[i]);
      hm.put(ar[i], val + 1);
    } else {
      hm.put(ar[i], 1);
    }

    print(hm.size());
  }

  //step 2: Iterate all other subarrays
  int s = 1, e = k;

  while (e < N) {
    //Remove ar[s-1]
    int val = hm[ar[s - 1]];
    hm[ar[s - 1]]--;

    if (hm.get[ar[s - 1]] == 0) {
      hm.remove(ar[s - 1]);
    }

    //add ar[e]
    if (hm.contains(ar[e])) {
      //Inc freq by 1
      int val = hm[ar[e]];
      hm[ar[e]]++;
    } else {
      hm.put(ar[e], 1);
    }

    print(hm.size());
    s++

  }
}

Complexity

Time Complexity: O(n)

Space Complexity: O(n)

---