Heaps 1: Introduction¶

Problem 1 Connecting the ropes¶

We are given an array that represents the size of different ropes. In a single operation, you can connect two ropes. Cost of connecting two ropes is sum of the length of ropes you are connecting. Find the minimum cost of connecting all the ropes.

To illustrate:

Example 1:

int A[] = {2, 5, 3, 2, 6}

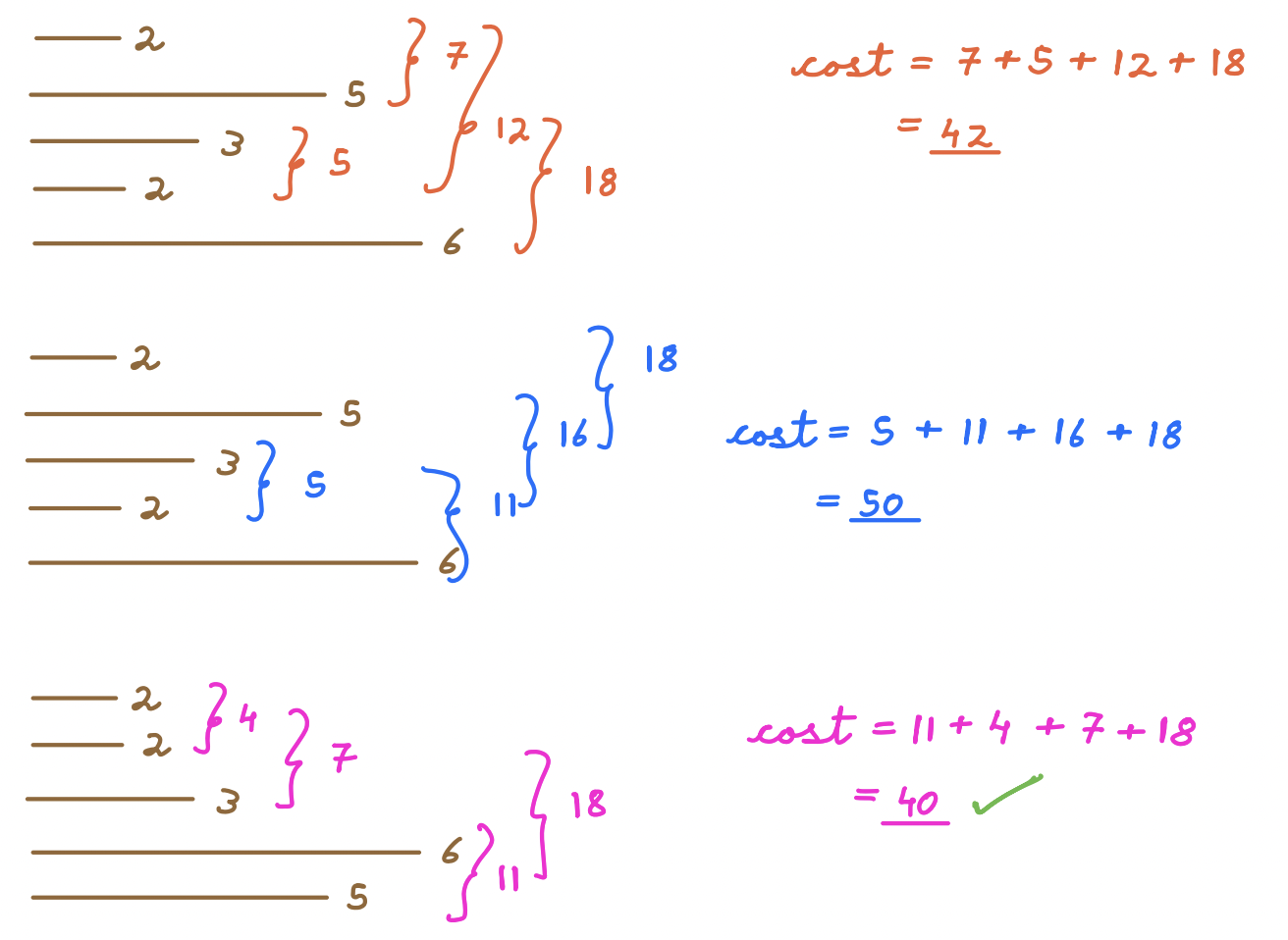
Example 2:

Initial Ropes: [2, 5, 6, 3]

Connect 2 and 5 (Cost = 2 + 5 = 7)
Total Cost: 7
New Ropes: [7, 6, 3]
Next Step: [7, 6, 3]

Connect 7 and 6 (Cost = 7 + 6 = 13)
Total Cost: 7 + 13 = 20
New Ropes: [13, 3]
Final Step: [13, 3]

Connect 13 and 3 (Cost = 13 + 3 = 16)
Total Cost: 20 + 16 = 36
Final Rope: [16]

This is one of the options for finding the cost of connecting all ropes, but we need to find the minimum cost of connecting all the ropes.

Observation¶

Say, we have 3 ropes, x < y < z
Which 2 ropes should we connect first ?

Case	1	2	3
Step 1	x+y	x+z	y+z
Step 2	(x+y) + z	(x+z) + y	(y+z) + x

Comparing case 1 and 2, y and z are different, now since y < z, we can say cost of 1 < cost of 2.

Comparing case 2 and 3, x and y are different, now since x < y, we can say cost of 2 < cost of 3.

Conclusion: Connecting smaller length ropes gives us lesser cost.

Process:¶

Initial Setup: Start with an array of rope lengths, e.g., [2, 2, 3, 5, 6]. First, sort the array.

Combining Ropes:

Continuously pick the two smallest ropes.
Combine these ropes, adding their lengths to find the cost.
Insert the combined rope back into the array at its correct position in sorted array.
Repeat until only one rope remains.

We are basically applying insertion sort.

Example Steps:

Combine ropes 2 and 2 (cost = 4). New array: [3, 4, 5, 6]. Total cost: 4.
Combine ropes 3 and 4 (cost = 7). New array: [5, 6, 7]. Total cost: 11.
Combine ropes 5 and 6 (cost = 11). New array: [7, 11]. Total cost: 22.
Combine ropes 7 and 11 (cost = 18). Final rope: 18. Total cost: 40.

Complexity¶

Time Complexity: O(N²)

Space Complexity: O(1)

Question¶

What is the minimum cost of connecting all the ropes for the array [1, 2, 3, 4]?

Choices

19
20
10
0

Explanation:

Always pick two of the smallest ropes and combine them.

After combining the two smallest ropes at every step, we need to sort an array again to get the two minimum-length ropes.

1, 2, 3, 4; cost = 3
3, 3, 4; sort: 3, 3, 4; cost = 6
6, 4; sort: 4, 6; cost = 10

Final Length: 10
Total Cost = (3 + 6 + 10) = 19

Warning

Please take some time to think about the solution approach on your own before reading further.....

Connecting the ropes optimisation¶

Heaps efficiently perform the necessary operations:

Insertion of elements in O(log n) time.
Extraction of the minimum element in O(log n) time.

NOTE: We'll understand how we can achive the above complexities, for now assume heap to be a black box solving the above requirements for us in lesser time.

Heap returns the min or max value depending upon it is a min heap or max heap.

Say, for above problem, we use a min heap. At every step, it will give us the 2 small length ropes. Please note below steps for solving above problem.

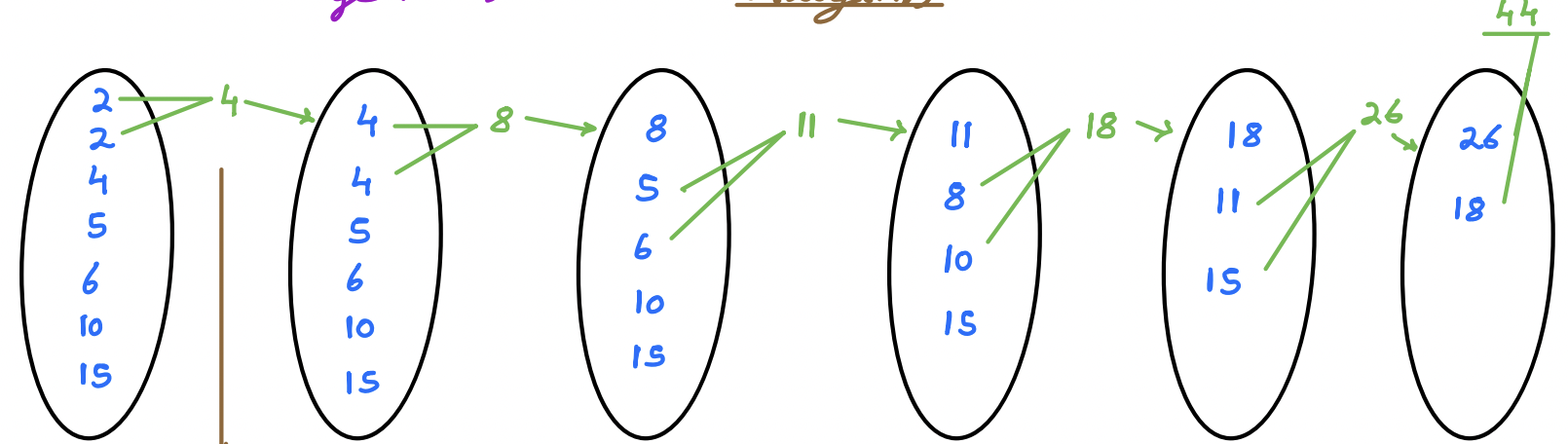
Time & Space Complexity¶

For every operation, we are removing 2 elements and inserting one back, hence it is 3 * log N. For N operations, the time complexity will be O(N * log N)

Space Complexity is O(N)

Heap Data Structure¶

The heap data structure is a binary tree with two special properties.

First property is based on structure.
- Complete Binary Tree: All levels are completely filled. The last level can be the exception but is should also be filled from left to right.
Second property is based on the order of elements.
- Heap Order Property: In the case of max heap, the value of the parent is greater than the value of the children. And in the case of min heap, the value of the parent is less than the value of the children.

Examples

Example 1:

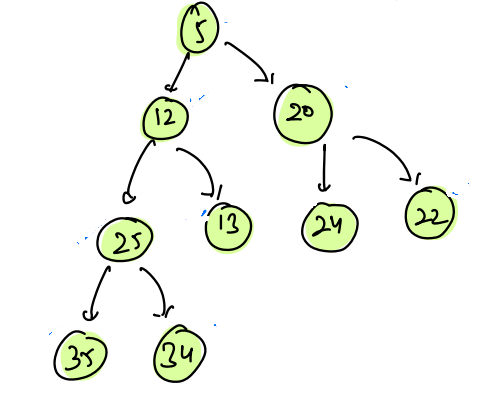
This is the complete binary tree as all the levels are filled and the last level is filled from left to right.
Heap Order Property is also valid at every point in the tree, as 5 is less than 12 and 20, 12 is less than 25 and 13, 20 is less than 24 and 22, 25 is less than 35 and 34.
Hence, it is a min-heap

Example 2:

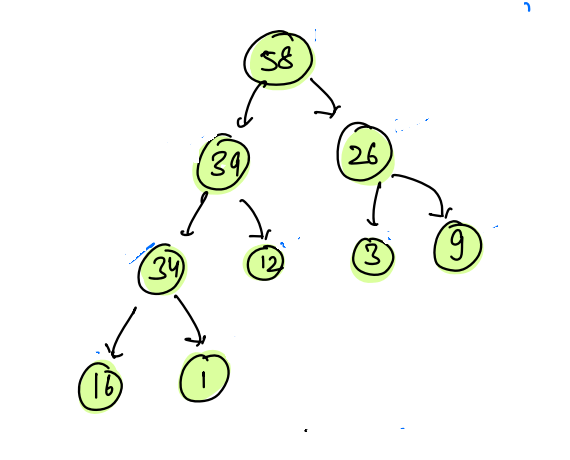
This is the complete binary tree as all the levels are filled and the last level is filled from left to right.
Heap Order Property is also valid at every point in the tree, as 58 is greater than 39 and 26, 39 is greater than 34 and 12, 26 is greater than 3 and 9, 34 is greater than 16 and 1.
Hence, it is a max-heap.

Array Implementation of Trees(Complete Binary Tree)¶

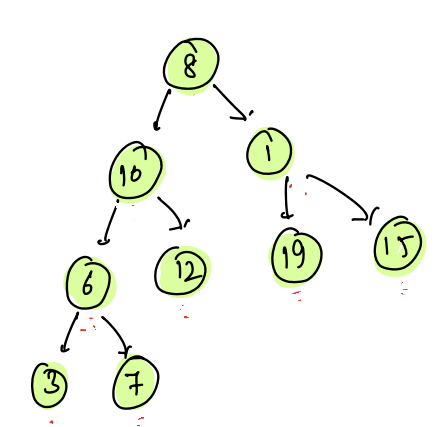
We shall store elements in the array in level order wise.
Such an array representation of tree is only possible if it is a complete binary tree.

Index 0 has its children at index 1 and 2
Index 1 has its children at index 3 and 4
Index 2 has its children at index 5 and 6
Index 3 has its children at index 7 and 8

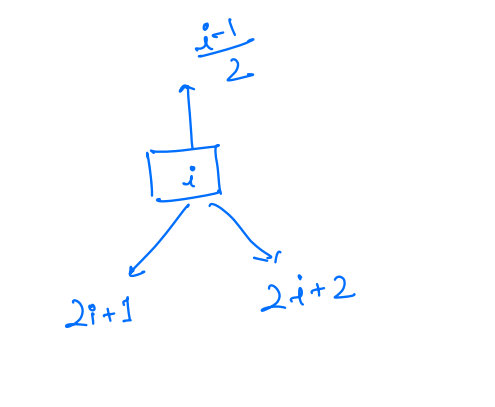
For the particular node stored at the i index, the left child is at (i * 2 + 1 ) and the right child is at (i * 2 + 2 ).

For any node i, its parent is at (i-1)/2.

Insertion in min heap¶

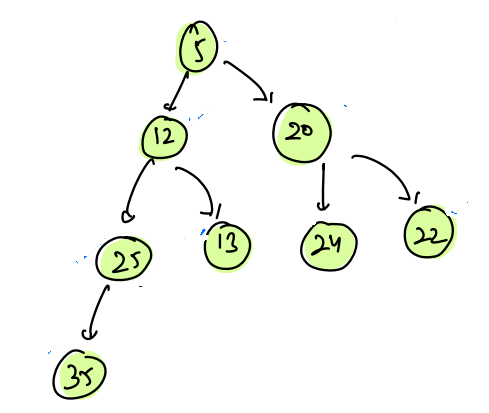
0	1	2	3	4	5	6	7
5	12	20	25	13	24	22	35

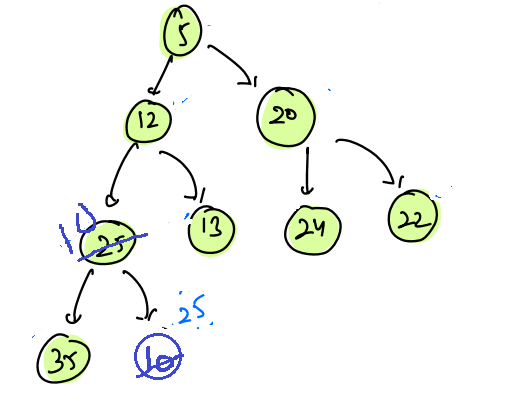
Example 1: Insert 10

In an array, if we will insert 10 at index 8, then our array becomes,

0	1	2	3	4	5	6	7	8
5	12	20	25	13	24	22	35	10

And the tree becomes,

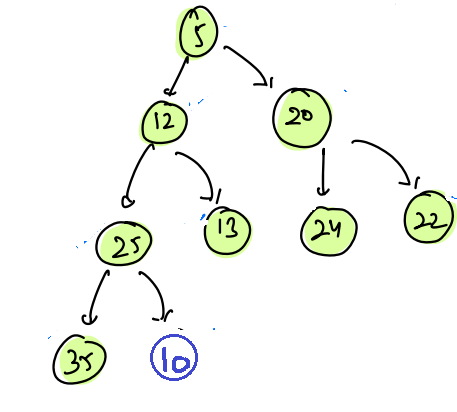
Now tree satisfies the complete binary tree property but the tree does not satisfy the min-heap property, as here 25 > 10.

In this case, we shall start with the inserted node and compare the parent with the child and keep swapping until the property is satisfied.

Let us assume the node inserted at index i and the index of its parent is pi.

if(arr[pi] > arr[i]) swap

i = 8
pi = (8-1)/2 = 3
Since, (arr[3] > arr[8]) swap

0	1	2	3	4	5	6	7	8
5	12	20	10	13	24	22	35	25

Now again we need to confirm whether the heap order property is satisfied or not by checking with its parent again.

i = 3
pi = (3-1)/2 = 1
Since, (arr[1] > arr[3]) swap

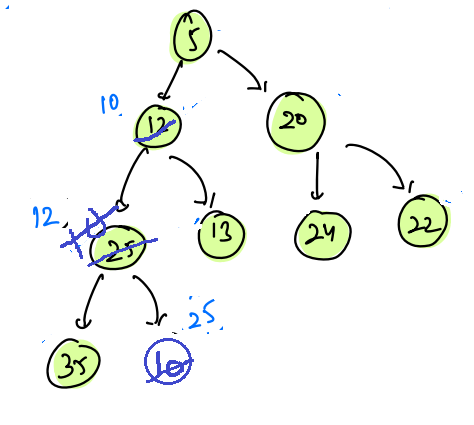
0	1	2	3	4	5	6	7	8
5	10	20	12	13	24	22	35	25

Now again we need to confirm whether the heap order property is satisfied or not by checking with its parent again.

i = 1
pi = (3-1)/2 = 0
Since, (arr[0] < arr[1]) no need to swap

STOP

Now this tree satisfies the min-heap order property.

0	1	2	3	4	5	6	7	8
5	10	20	12	13	24	22	35	25

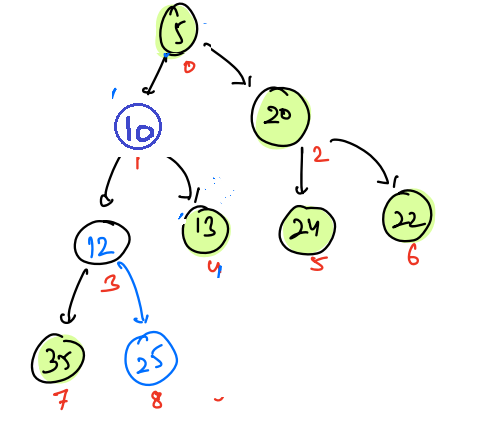
Example 2: Insert 3

First insert 3 at index 9.

0	1	2	3	4	5	6	7	8	9
5	10	20	12	13	24	22	35	25	3

Compare index 9 and parent index ((9-1)/2)= 4 value, as arr[4] > arr[9], swap.
Now again compare index 4 and , parent index((4-1)/2)=1 arr[1]>arr[4], swap again.
Now again compare index 1 and , parent index((1-1)/2)=0 arr[0]>arr[1], swap again.
Now zero index does not have any parent so stop.

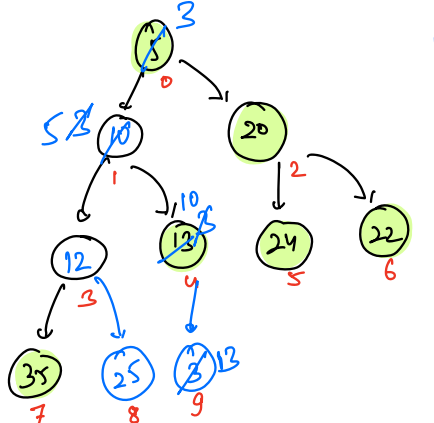
0	1	2	3	4	5	6	7	8	9
3	5	20	12	10	24	22	35	25	13

NOTE: The maximum swap we can perform for any element to be inserted is equal to the height of the tree.

Question¶

Time Complexity of inserting an element in a heap having n nodes?

Choices

O(1)
O(log n)
O(sqrt n)
O(n)

Inserting in min heap pseudocode¶

Pseudocode¶

heap[];
heap.insert(val); // inserting at last
i = heap.size - 1;
while (i > 0) {
    pi = (i - 1) / 2;
    if (heap[pi] > heap[i]) {
        swap(heap, pi, i);
        i = pi;
    } else {
        break;
    }
}

Complexity¶

Time Complexity: O(height of tree) = O(logN)

Extract Min¶

Min Heap -

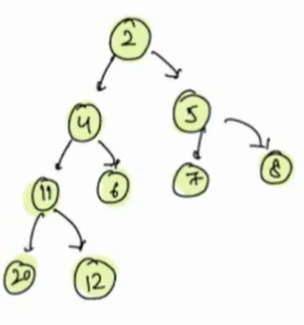
0	1	2	3	4	5	6	7	8
2	4	5	11	6	7	8	20	12

In this tree, we have a minimum element at the root. First we swap the first and last elements, then remove the last index element of an array virtually, i.e. consider your array from index 0 to N-2.

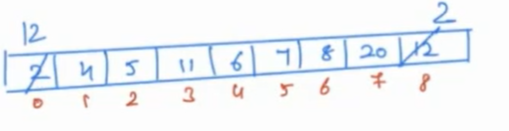
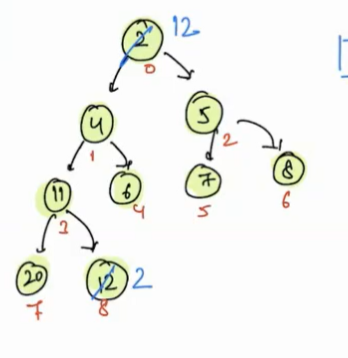
But the tree is not satisfying the heap-order property. To regain this heap-order property, first check 12, 4 and 5, the minimum is 4, so swap 12 with 4.

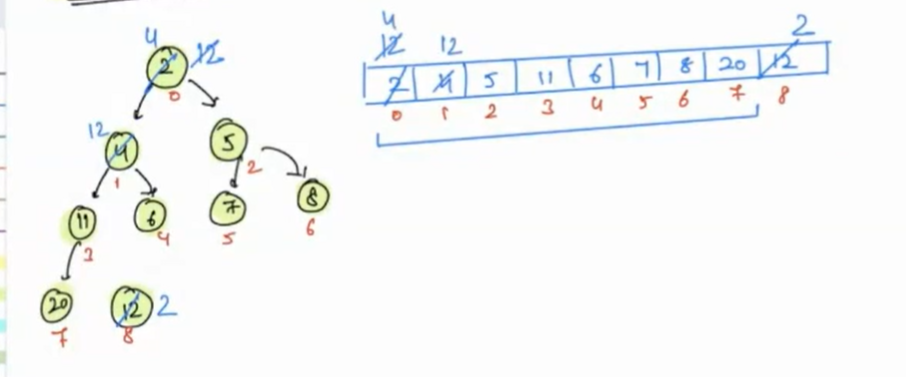
Now check the index 1(12) value, it greater than index 3(11) and index 4(6), so we need to swap this value with the minimum of left and right child i.e. 6.

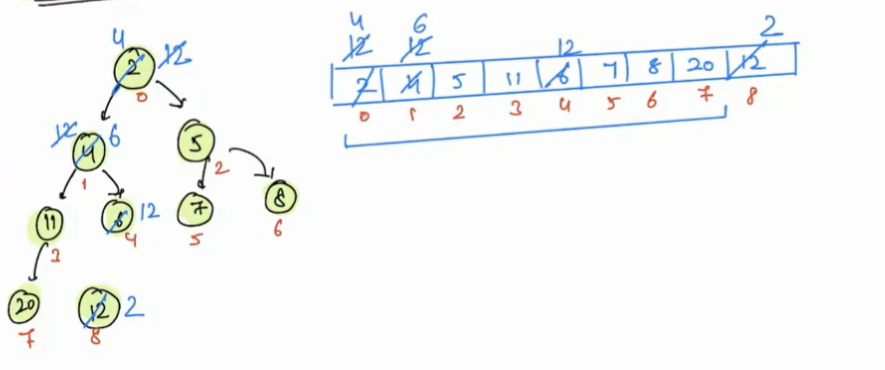
Now index 4(12) does not have any child, so we will stop here. Now the heap-order property is regained.

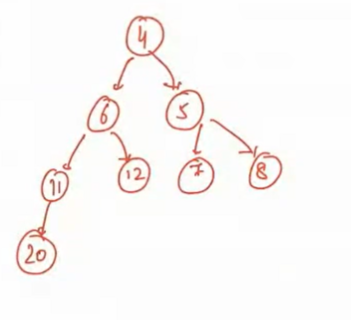
NOTE to Instructor: Perform extract-min again for more clarity on above tree.

Pseudocode¶

swap(heap, 0, heap - size() - 1)
heap.remove(heap.size() - 1)
heapify(heap[], 0);

void heapify(heap[], i) {
    while (2 i + 1 < N) { //need to handle the edge case when left child is there but not the right child
        x = min(heap[i], heap[2 i + 1], heap[2 i + 2])

        if (x == heap[i]) {
            break
        } else if (x == heap[2 i + 1]) {
            swap(heap, i, 2 i + 1)
            i = 2 i + 1
        } else {
            swap(heap, i, 2 i + 2)
            i = 2 i + 2
        }
    }
}

Complexity¶

Time Complexity: O(log N)

Build a heap¶

We have an array of values, we want to make a heap of it.
[5, 13, -2, 11, 27, 31, 0, 19]

Idea 1¶

Sort the array.

[-2, 0, 5, 11, 13, 19, 27, 31]

Looking at the tree below, we can see this is a heap.

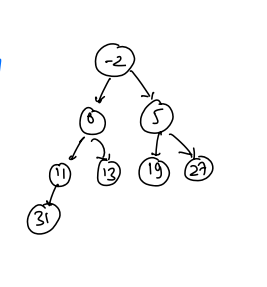
Time Complexity: O(N * logN)

Idea 2¶

Call insert(arr[i]) for every element of an array.

Explanation:

When insert(val) is called, at every insert we shall make sure heap property is being satisfied.

It will take N * logN, as for each element, we will take O(log N) as heapify shall be called.

Time Complexity:O(N * logN)

--

Build a heap Idea 3¶

Idea to build in linear time¶

We have an array
[7, 3, 5, 1, 6, 8, 10, 2, 13, 14, -2]

We can represent this array in the form of a tree.

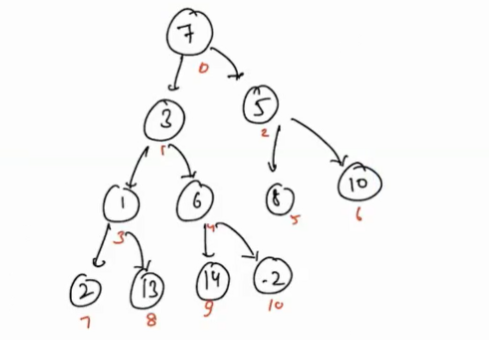
In the above tree, the heap-order property is automatically valid for the leaf node, hence no need to heapify them.
Rather, we shall start with the first non-leaf node.
The first non-leaf is nothing but the parent of the last leaf node of the tree and the index of the last node is \(n-1\), so the index of the first non-leaf is \(((n-1-1)/2)=((n-2)/2)=(n/2)-1\).
We will call heapify() starting from for \((n/2)-1\) index to index 0.

for (int i = (n / 2) - 1; i >= 0; i--) {
    heapify(heap[], i);
}

Firstly it will call for i = 4(6), heapfiy(heap[], 4), minimum of 6, 14, -2 is -2 so 6 and -2 will be swapped.

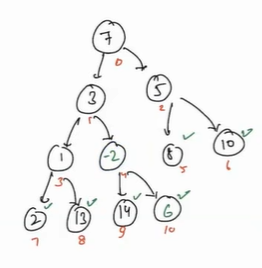
Now 6 does not have any children so we will stop here.
Call heapify for i = 3(1), now we will check minimum of 1, 2, 13 is 1, so here min-heap property is already satisfied.
Call heapify for i = 2(5), minimum of 5, 8, 10 is 5 and it is at index 2, so here min-heap property is already satisfied.
Call heapify for i = 1, minimum of 3, 1, -2 is -2 and so swap.

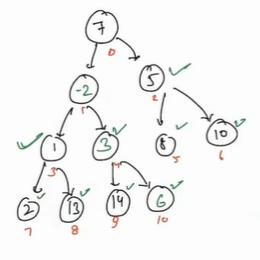
Now we will again check for 3, and 3 is less than 14 and 6, so here heap-order property is valid here.
Call heapify for i = 0, here also heap-order property is not satisfied as -2 is less than 7, so swap.

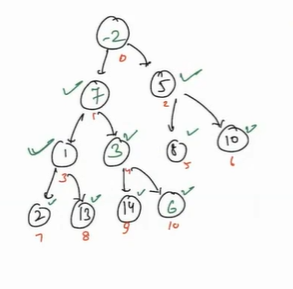
Now again check for 7, here minimum of 7, 1 and 3 is 1, so again swap it.

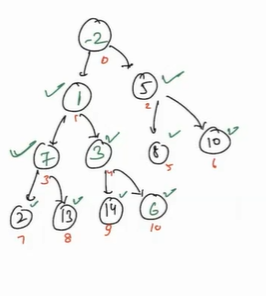
Now again check for minimum of 7, 2 and 13 is 2, so again swap it.

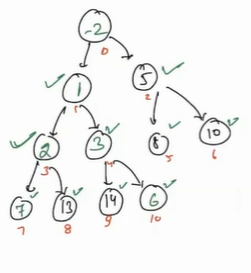
Now 7 does not have any child so stop here.
Now all the nodes has valid heap-order property.

Time Complexity¶

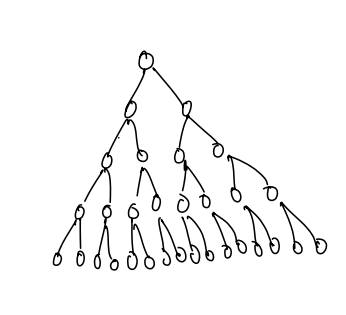
Total Number of elements in tree = N
Elements at last level = N/2

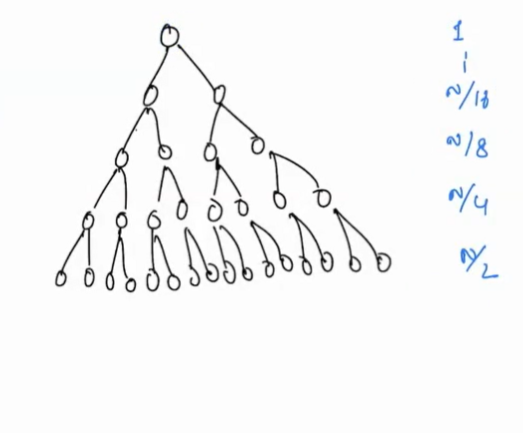
We are not calling heapify() for the last level(leaf node), So for the leaf node, total swaps are 0.
For the last second level, we have N/4 nodes and at maximum, there can be 1 swap for these nodes i.e. with the last level.
And maximum swaps for N/8 level nodes 2.
Similar, for the root node, maximum swaps can be equal to the height of the tree.

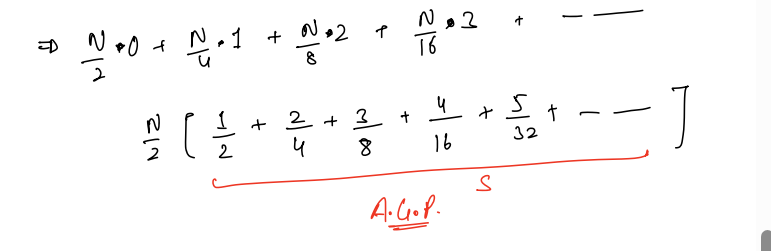
Here it is an Arithmetic Geometric progression. We need to find the sum of

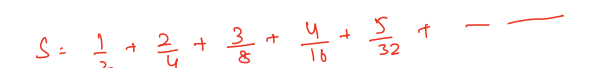
Multiply both sides by ½

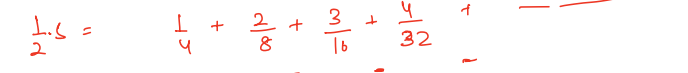
Now subtract the above two equations

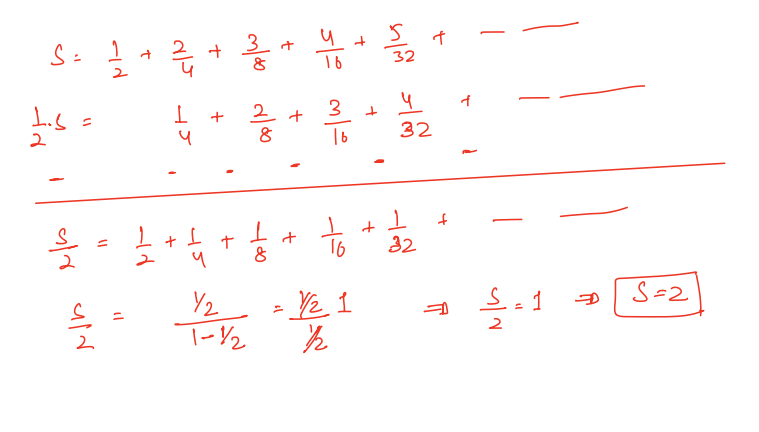
Here we are using the formula of the sum of GP.

And put the value of the sum in this equation

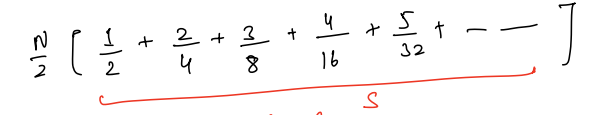
Then
(N/2) * 2
Here both will cancel out with each other and so our overall time complexity for building a heap is O(N)

Question¶

What is the time complexity for building a heap with N nodes?

Choices

O(1)
O(N\(^2\))
O(N)
O(logN)

Merge N-sorted arrays¶

a - [2, 3, 11, 15, 20]
b - [1, 5, 7, 9]
c - [0, 2, 4]
d - [3, 4, 5, 6, 7, 8]
e - [-2, 5, 10, 20]

We have to merge these sorted arrays.

Idea¶

If we want to merge two sorted arrays then we need two pointers.
If we want to merge three sorted arrays then we need three pointers.
If we want to merge N sorted arrays then we need N pointers, in which complexity becomes very high and we need to keep track of N pointers.

Question¶

For merging N sorted arrays, which data structure would be the most efficient for this task ?

Choices

Linked List
Array
Min-Heap
Hash Table

Explanation:

A Min-Heap is an efficient data structure choice. The Min-Heap ensures that the smallest element among all the elements in the arrays is always at the front. This allows for constant-time access to the minimum element, making it efficient to extract and merge elements in sorted order.

Warning

Please take some time to think about the optimised approach on your own before reading further.....

Optimized Solution¶

First, we need to compare the 0^th index element of every array.
Now we use heap here.
We will add an index 0 element of every array in the heap, in the form of element value, array number and Index of the element in particular.

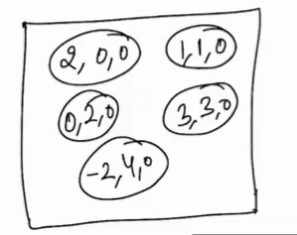
Now take the minimum element and insert it in the resultant array,

Now insert the next element of the list for which the minimum element is selected, like first, we have taken the fourth list element, so now insert the next element of the fourth list.

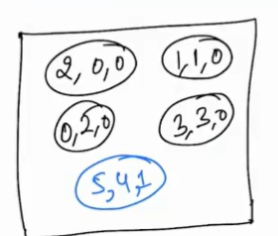
Now again extract-min() from the heap and insert the next element of that list to which the minimum element belongs.
And keep repeating this until we have done with all the elements.

Time Complexity¶

Time Complexity: (XlogN) Here X is a total number of elements of all arrays.