Advanced DSA: Arrays 3 - Interview Problems¶
Merge Intervals¶
An Interval is defined by start and end time, where start <= end.
Say we are given a list of Intervals, we will have to merge them if they overlap.
Let's look at them below -
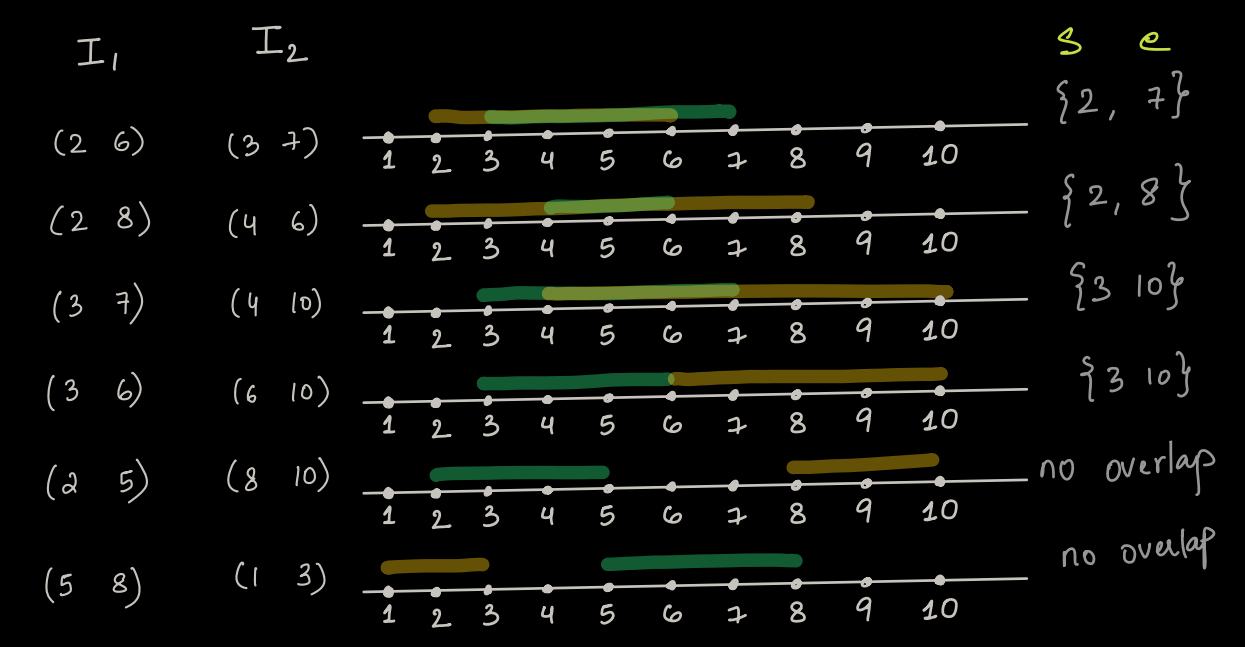
Non-Overlapping Condition¶
Say there are two Intervals, I1 {s1 e1} & I2 {s2 e2} Then the condition for them to not overlap is -
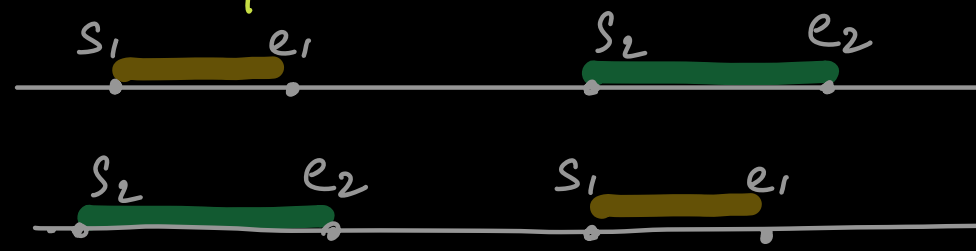
if(s2 > e1 || s1 > e2)
So, if above condition is not followed, it says that Intervals are overlapping!
How to merge overlapping Intervals ?¶
[I1.start , I1.end] & [I2.start , I2.end]
After merging -
[min(I1.start, I2.start) , max(I1.end, I2.end)]
Question¶
If the intervals [3, 8] and [5, 12] are given, do they overlap?
Choices
- Yes
- No
Explanation:¶
Answer: Yes
The intervals [3, 8] and [5, 12] overlap because 8 is greater than 5. The overlapping area is [5, 8]
Question¶
What is the correct way to represent the merged result of intervals [6, 10] and [8, 15]?
Choices
- [6, 15]
- [6, 8, 10, 15]
- [6, 10] and [8, 15]
- [8, 10]
Explanation:¶
[6, 15]
This is because the merging of intervals involves combining overlapping intervals into a single, continuous interval
Problem 1 : Merge sorted Overlapping Intervals¶
Problem Statement
Given a sorted list of overlapping intervals, sorted based on start time, merge all overlapping intervals and return sorted list.
Input:
Interval[] = {(0,2), (1,4), (5,6), (6,8), (7,10), (8,9), (12,14)}
Output:
{(0,4), (5,10), (12,14)}
Explanation:¶
| Interval 1 | Interval 2 | Answer Interval List | |
|---|---|---|---|
| 0-2 | 1-4 | Overlapping | 0-4 |
| 0-4 | 5-6 | Not Overlapping | 0-4, 5-6 |
| 5-6 | 6-8 | Overlapping | 0-4, 5-8 |
| 5-8 | 7-10 | Overlapping | 0-4, 5-10 |
| 5-10 | 8-9 | Overlapping | 0-4, 5-10 |
| 5-10 | 12-14 | Not Overlapping | 0-4, 5-10, 12-14 |
The Array Is Sorted Based on Start Time. What Is the Overlapping Condition?¶
Say start time of A < start time of B
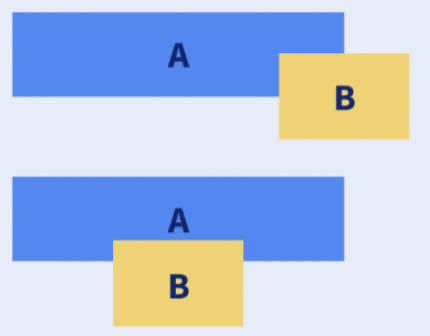
Overlapping Condition -
If start of B <= end of A
Question¶
Given a sorted list of overlapping intervals, sorted based on start time, merge all overlapping intervals and return sorted list.
Input:
Interval[] = { (1,10), (2, 3), (4, 5), (9, 12)}
Choices
- (1, 12)
- (1, 10), (9, 12)
- (1, 9), (9, 12)
- No Change
Problem 1 Approach¶
- Create an array to store the merged intervals.
- If the current and ith intervals overlaps, merge them. In this case update the current interval with the merged interval.
- Else, insert the current interval to answer array since it doesn't overlap with any other interval and update the current Interval to ith Interval.
Dry Run¶
Input:
Interval[] = {(0,2), (1,4), (5,6), (6,8), (7,10), (8,9), (12,14)}
Explanation:¶
| current | ith | After merging | answer list | |
|---|---|---|---|---|
| 0-2 | 1-4 | Overlapping | 0-4 | |
| 0-4 | 5-6 | Not Overlapping | Not needed | 0-4 |
| 5-6 | 6-8 | Overlapping | 5-8 | 0-4 |
| 5-8 | 7-10 | Overlapping | 5-10 | 0-4 |
| 5-10 | 8-9 | Overlapping | 5-10 | 0-4 |
| 5-10 | 12-14 | Not Overlapping | Not needed | 0-4, 5-10 |
| 12-14 | end |
At the end, we are left with the last interval, so add it to the list.
Pseudocode¶
//Already a class/structure will be present for Interval
//We will only need to create an answer array of type Interval
list < Interval > ans;
// Current Segment
int cur_start = A[0].start, cur_end = A[0].end;
for (int i = 1; i < A.size(); i++) {
// if i'th interval overlaps with current interval
if (A[i].start <= cur_end) {
// merging them
cur_end = max(cur_end, A[i].end);
} else {
//adding current interval to answer.
//create a new Interval
Interval temp(cur_start, cur_end); //if struct is declared, otherwise if class is declared then we can simply use new keyword
ans.push_back(temp);
// update cur Interval to ith
cur_start = A[i].start;
cur_end = A[i].end;
}
}
Interval temp(cur_start, cur_end);
ans.push_back(temp);
return ans;
Complexity¶
Time Complexity: O(N)
Space Complexity: O(1)
Problem 2 Sorted Set of Non Overlapping Intervals¶
Given a sorted list of overlapping intervals based on start time, insert a new interval such that the final list of intervals is also sorted and non-overlapping. Print the Intervals.
Example 1:
N = 9
(1,3)
(4,7)
(10,14)
(16,19)
(21,24)
(27,30)
(32,35)
(38,41)
(43,50)
New Interval
(12, 22)
Explanation:
| ith | new Interval | Overlaps? | |
|---|---|---|---|
| (1,3) | (12,22) | No | (1,3) |
| (4,7) | (12,22) | No | (4,7) |
| (10,14) | (12,22) | Yes; merged: (10,22) | |
| (16,19) | (10,22) | Yes; merged: (10,22) | |
| (21,24) | (10,22) | Yes; merged: (10,24) | |
| (27,30) | (10,22) | No; small new Interval gets printed first | (10,22) |
| (32,35) | (32,35) | ||
| (38,41) | (38,41) | ||
| (43,50) | (43,50) |
Please Note: Once the new Interval gets printed, all the Intervals following it also gets printed.
More Examples
Example 2:
N = 5
(1,5)
(8,10)
(11,14)
(15,20)
(21,24)
New Interval
(12, 24)
| ith | new Interval | Overlaps? | |
|---|---|---|---|
| (1,5) | (12, 24) | No | (1,5) |
| (8,10) | (12, 24) | No | (8,10) |
| (11,14) | (12, 24) | Yes; merged:(11, 24) | |
| (15,20) | (11, 24) | Yes; merged:(11, 24) | |
| (21,24) | (11, 24) | Yes; merged:(11, 24) |
We are done with all the intervals but left the new Interval at the end; in this case we have to print the new Interval.
Example 3:

Question¶
If the sorted set of non-overlapping intervals is [1, 5], [6, 10], and [12, 15], what happens if you add the interval [4, 7] such that the final list of intervals is also sorted and non-overlapping.?
Choices
- [1, 10] and [12, 15]
- [1, 5], [4, 7], [6, 10], [12, 15]
- [1, 5] and [6, 10] only
- No change
Explanation:¶
(1,5)
(6,10)
(12,15)
New Interval
(4, 7)
| ith | new Interval | Overlaps? | |
|---|---|---|---|
| (1,5) | (4, 7) | Yes; merged:(1, 7) | |
| (6,10) | (1, 7) | Yes; merged:(1, 10) | |
| (12,15) | (1, 10) | No; small new Interval gets printed first | (1, 10) |
| (12,15) | (12, 15) |
Thus after merging, the intervals are [1, 10] and [12, 15]
Problem 2 Pseudocode¶
void merge(int Interval[], int nS, int nE) {
for (int i = 0; i < N; i++) {
int L = Interval[i].start, R = Interval[i].end;
//Not Overlapping
if (nS > R) {
print({
L,
R
});
}
// new Interval is not overlapping and is smaller
// print new Interval and then all the remaining Intervals
else if (L > nE) {
print({
nS,
nE
});
for (int j = i; j < N; j++) {
print({
Interval[j].start,
Interval[j].end
})
}
return;
} else {
nS = min(L, nS);
nE = max(R, nE);
}
}
print({
nS,
nE
});
}
Complexity¶
Time Complexity: O(N)
Space Complexity: O(1)
Problem 3 Find First Missing Natural Number¶
Given an unsorted array of integers, Find first missing Natural Number.
Examples
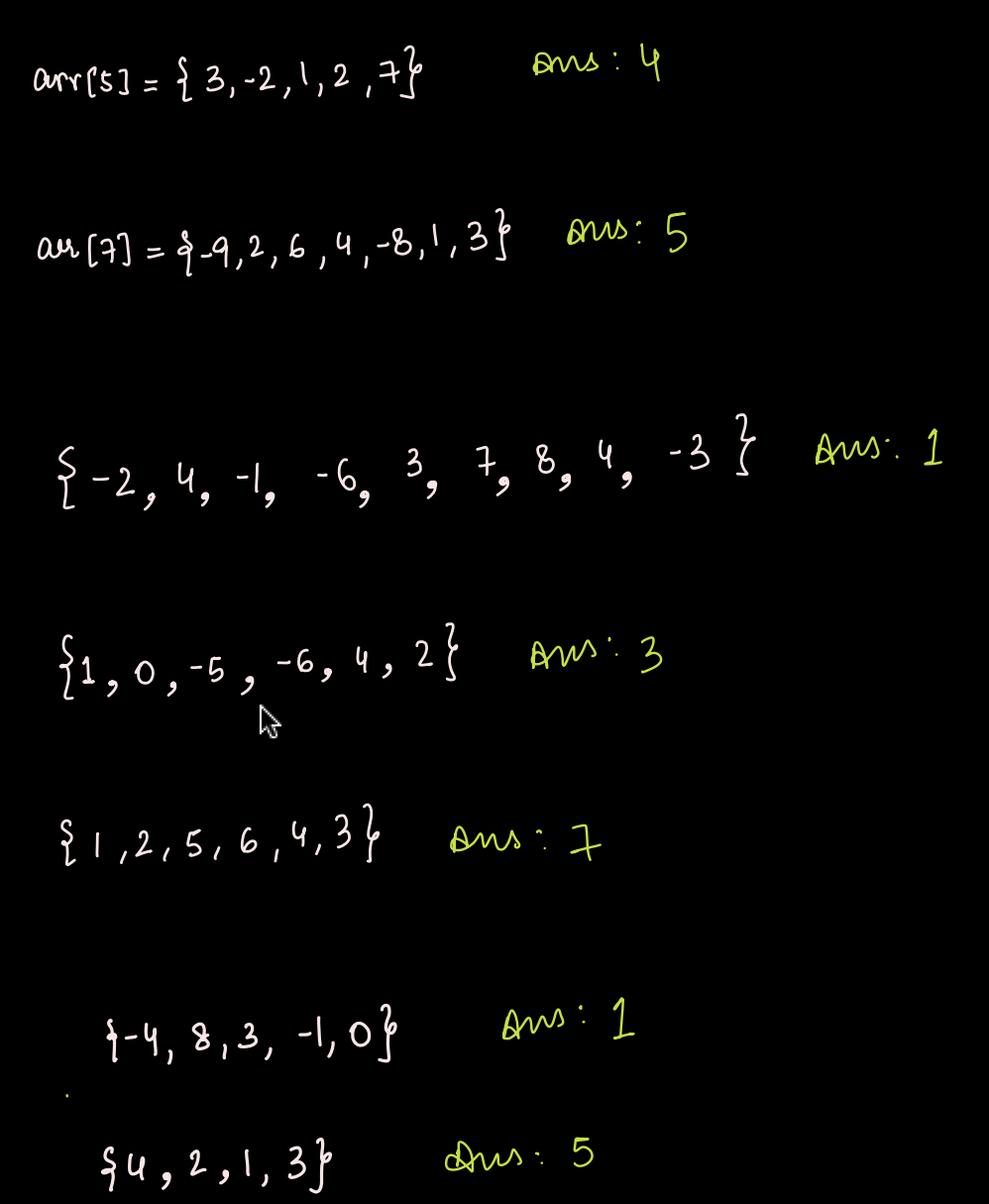
Question¶
In the array [5, 3, 1, -1, -2, -4, 7, 2], what is the first missing natural number?
Choices
- 4
- 6
- -3
- 8
Warning
Please take some time to think about the solution approach on your own before reading further.....
Find First Missing Natural Number Solution Approach¶
Approach 1: Brute Force¶
Check for all the numbers from 1 till we get the answer
T.C - O(N * ans)
Here, in the worst case answer can go uptil N+1, in case if all numbers from 1 to N are present in the array.
Example - {4, 1, 3, 2}
Here we will have to iterate till 5, ie. N+1.
Idea¶
Can we utilise the fact that answer can be out of 1 to N+1?
If any number other than 1 to N is present, then missing is out of 1 to N only.
If all elements from 1 to N are present, then it will be N+1.
Say we start checking if 1 is present or not, we somehow want to mark the presence of 1.
Now, since we can't use extra space, so we can use indices to mark the presence of a number.
Index 0 can be used to mark presence of 1.
Index 1 can be used to mark presence of 2.
Index 2 can be used to mark presence of 3.
so on....
Now how do we mark the presence ?
One Solution:
We can set element at that index as negative.
But what if negative number is part of the input?
Let's assume only positive numbers are present
We can use indices to mark the presence of a number.
We can set element at that index as negative.
A[ ] = {8, 1, 4, 2, 6, 3}
N = 6
Answer can be from [1 7]
So, if any number is beyond this range, we don't care!
| index | element | presence marked at index | state of the array |
|---|---|---|---|
| 0 | 8 | don't care, since out of answer range | |
| 1 | 1 | 0 | {-8, 1, 4, 2, 6, 3} |
| 2 | 4 | 3 | {-8, 1, 4, -2, 6, 3} |
| 3 | 2 | 1 | {-8, -1, 4, -2, 6, 3} |
| 4 | 6 | 5 | {-8, -1, 4, -2, 6, -3} |
| 5 | 3 | 2 | {-8, -1, -4, -2, 6, -3} |
Now, we can just iterate from left to right and whichever element is not ve-, we can return i+1 as the answer.
Example: {-8, -1, -4, -2, 6, -3}
Here, index: 4 is +ve, hence 5 is the answer.
NOTE: Since we are marking elements as negative, so when checking presence of a certain number, we'll have to consider the absolute value of it.
Pseudocode¶
for (int i = 0; i < N; i++) {
int ele = abs(A[i]);
if (ele >= 1 && ele <= N) {
int idx = ele - 1;
A[idx] = -1 * abs(A[i]);
}
}
Find First Missing Natural Number For Negative Numbers¶
How to resolve for negative numbers ?¶
Will negatives ever be our answer?
NO!
So, we don't have to care about them!
Should we change them to ve+ ?
NO! They may fall in our answer range.
Should we mark them 0?
NO! Then we will not be able to mark the presence of a number!
We can just change negative number to a number that is out of our answer range. It can be N+2.
for (int i = 0; i < N; i++) {
if (A[i] <= 0) {
A[i] = N + 2;
}
}
for (int i = 0; i < N; i++) {
int ele = abs(A[i]);
if (ele >= 1 && ele <= N) {
int idx = ele - 1;
A[idx] = -1 * abs(A[i]);
}
}
for (int i = 0; i < N; i++) {
if (A[i] > 0) return i + 1;
}
return N + 1;
Please show a dry run on - {4, 0, 1, -5, -10, 8, 2, 6}
Complexity¶
Time Complexity: O(N)
Space Complexity: O(1)
