Linked List 1: Introduction¶

Linked List¶

Issues with Array¶

We need continuous space in memory to store Array elements. Now, it may happen that we have required space in chunks but not continuous, then we will not be able to create an Array.

Linked List¶

A linear data structure that can utilize all the free memory
We need not have continuous space to store nodes of a Linked List.

Representation of Linked List¶

it has a data section where the data is present
a next pointer which points to next element of the linked list

Structure of Linked List¶

class Node{
    int data;
    Node next;
    Node(int x){
        data = x;
        next = null;
    }
}

Example of Linked List

the first node of the linked list is called head
any linked list is represented by its first node

Question¶

Where will the "next" pointer of the last node point to?

Choices

First Node
Any Node
Middle Node
Null

Question¶

From which node can we travel the entire linked list ?

Choices

Middle
First
Last
Any Node

Operation on Linked List¶

1. Access kth element(k = 0; k is the first element)¶

Node temp = Head // temp is a compy
for i -> 1 to k {
    temp = temp.next
}
return temp.data // never update head otherwise the first node is lost

Time complexity to access the kth element is O(K). Here we can see that linked list takes more time compared to array as it would take constant time to access the kth element.

2. Check for value X (searching)¶

We can simply iterate and check if value X exists of not.

temp = Head
while (temp != null){
    if(temp.data == X)
    return true
    temp = temp.next
}
return false

Here if the Linked List is empty i.e if Head = NULL, if we try to access head.next it will give null pointer expection error.

Time Complexity for searching in Linked list is O(N).

In linked list we cannot perform binary search because we have to travel to the middle element. We cannot jump to the middle element unlike array.

Question¶

What is the time complexity to search any node in the linked list?

Choices

O(1)
O(log(N))
O(N)
O(N²)

Question¶

What is the time complexity to access the Kth element of the linked list? [index K is valid]

Choices

O(1)
O(log(N))
O(N)
O(K)

Problem 1 Insert a New Node with Data¶

Insert a New Node with Data¶

Insert a new node with data v at index p in the linked list

Though indexing doesn't exist is LL, but for our understanding, let's say Node 1 is at index 0, Node 2 at index 1, etc.

Testcase 1

v = 60 and p = 3

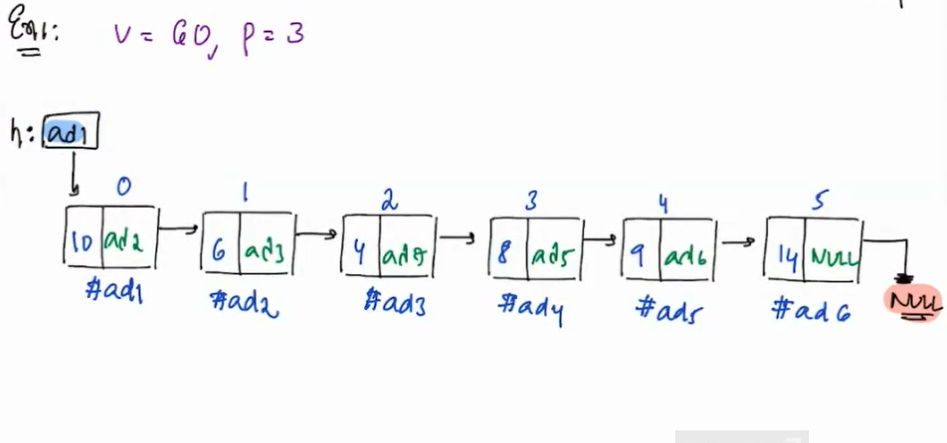
Solution to Testcase 1

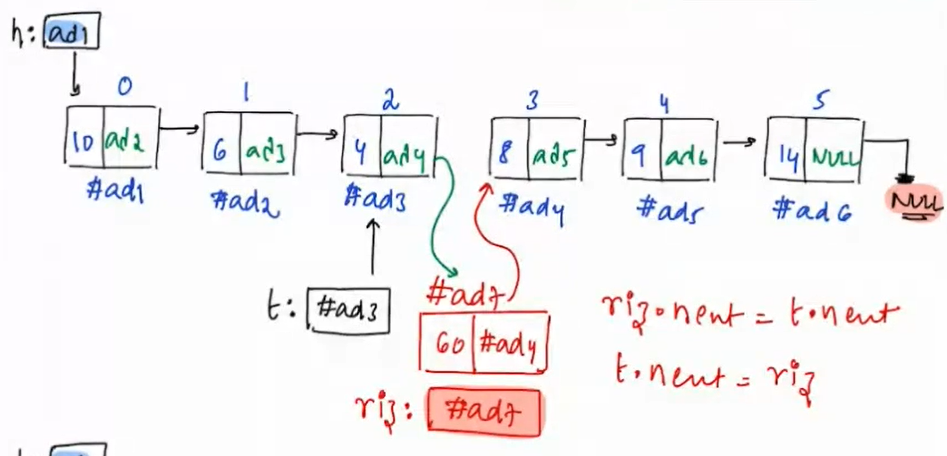
Iterate to the node having index p-1 where p-1>=0 from start of linked list. Here p is 3 so we iterate till 2
On reaching index 2 we create a new node riz with data v i.e. 60
Set riz.next = t.next and set t.next = riz

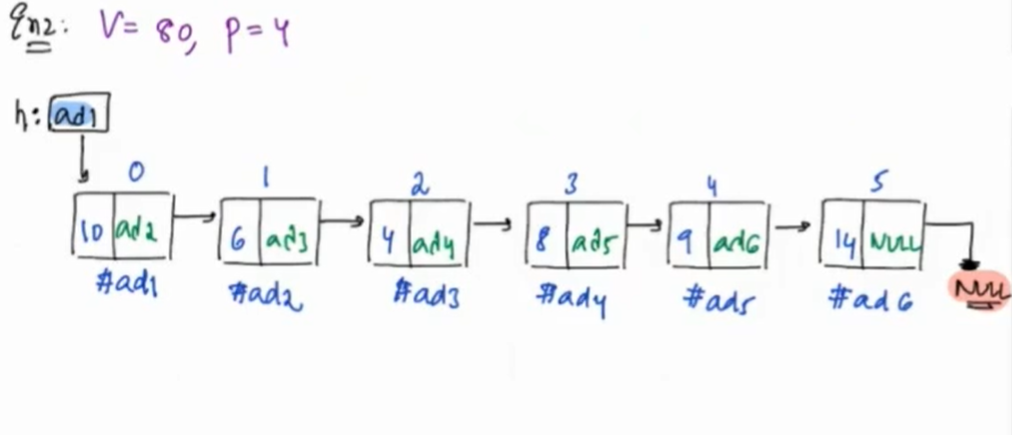
Testcase 2

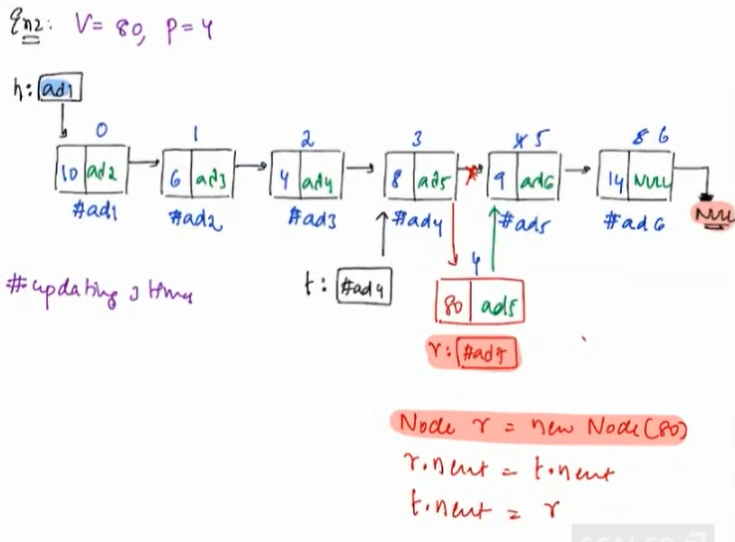
Solution to Testcase 2

We can do the dry run similar to testcase 1 here is the final result

Question¶

Insert a new node with data 10 at index 2 in the Given linked list.

Head -> 1 -> 6 -> 7 -> 9 -> Null

Choose the correct LinkedList after insertion.

Choices

Head -> 1 -> 6 -> 7 -> 9 -> 10 -> Null
Head -> 1 -> 6 -> 10 -> 7 -> 9 -> Null
Head -> 1 -> 10 -> 6 -> 7 -> 9 -> Null
Head -> 10 -> 1 -> 6 -> 7 -> 9 -> Null

Insert a New Node with Data Approach¶

Approach¶

Traverse till (p - 1)th node. Let's call it t.
Create a new node newNode, with data v.
Set newNode.next equals to t.next.
Set t.next to reference of newNode.

Pseudocode 1¶

Function insertAtIndex(p, v, Node head) {
  Node t = head
  for (i = 1; i < p; i++) // iterating updating t, p-1 times
  {
    t = t.next
  }

  // create a new node
  Node newNode = Node(v)

  // Inserting the Node
  newNode.next = t.next
  t.next = newNode
}

Again there is an edge case to above solution can anyone figure it out ?

Edge Case¶

If p = 0 then where to insert the node ?

=> At head of the list.

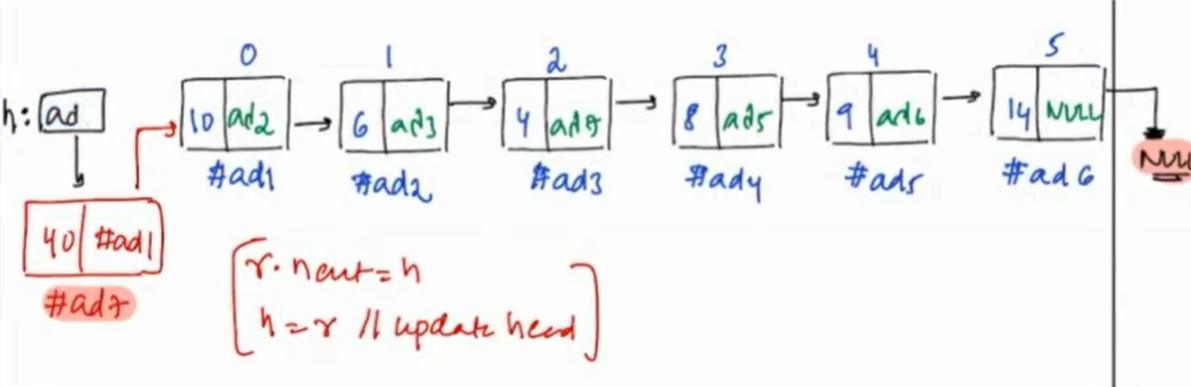
Pseudocode 2¶

Function insertAtIndex(p, v, Node head) {
  // create a new node
  Node newNode = Node(v)

  Node t = head

  if (p == 0) { // edge case
    newNode.next = head
    head = newNode
  }

  for (i = 1; i < p; i++) { // iterating updating t p-1 times
    t = t.next
  }

  // Inserting the Node
  newNode.next = t.next
  t.next = newNode
}

Time Complexity for Insertion¶

O(K)

Deletion in Linked List¶

Delete the first occurrence of value X in the given linked list. If element is not present, leave as is.

Example 1:

List: 1 -> 8 -> 4 -> -2 -> 12
X = -2

Ans:
List: 1 -> 8 -> 4 -> 12
-2 has been deleted from the list.

Example 2:

List: 1 -> 8 -> 4 -> -2 -> 4 -> 12
X = 4

Ans:
List: 1 -> 8 -> -2 -> 4 -> 12
The first occurrence of 4 has been deleted from the list.

Cases:¶

Empty list i.e., head = null

List: null
X = 4

Ans:
List: null

head.data = X i.e., delete head

List: 4
X = 4

Ans:
List: null

X is somewhere in between the list, find and delete node with value X

List: 1 -> 8 -> 4 -> -2 -> 4 -> 12
X = 4

Ans:
List: 1 -> 8 -> -2 -> 4 -> 12 (removed first occurrence)

X is not in the list, simply return

List: 1 -> 8 -> -2 -> 7 -> 12
X = 4

Ans:
List: 1 -> 8 -> -2 -> 7 -> 12

Question¶

Delete the first occurrence of value X in the given linked list. If element is not present, leave as is.

Linked List : 5 -> 4 -> 7 -> 1 -> NULL
X (to Delete) : 1

Choices

5 -> 4 -> 7 -> 1 -> NULL
5 -> 4 -> 7 -> NULL
4 -> 7 -> 1 -> NULL
5 -> 7 -> NULL

Explanation:

The Value 1 is not present in the Linked List. So leave as it is.

Thus, the final Linked List is 5 -> 4 -> 7 -> -1 -> NULL

Deletion in Linked List Approach and Pseudocode¶

Approach¶

Check if the list is empty; if so, return it as is.
If the target value X is at the head, update the head to the next node.
Otherwise, iterate through the list while looking for X.
When X is found, skip the node containing it by updating the next reference of the previous node.
Return the modified head (which may or may not have changed during the operation).

Pseudocode¶

if (head == null) return head
if (head.data == X) {
  tmp = head
  free(tmp) //automatically done in java, whereas have to do manually for c++ and other languages.
  head = Head.next
  return head
}
temp = head
while (temp.next != null) {
  if (temp.next.data == X) {
    tmp = temp.next
    temp.next = temp.next.next
    free(tmp)
    return head
  }
  temp = temp.next
}
return head

Time complexity for Deletion¶

O(N)

It can be seen that every operation in linked list takes linear time complexity unlike arrays.

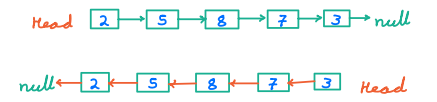
Problem 3 Reverse the linked list¶

Note: We can't use extra space. Manipulate the pointers only.

Example

Warning

Please take some time to think about the solution approach on your own before reading further.....

Approach:¶

Check for Empty List:
- If head is null, return it as is.
Handle Single Node List:
- If head.next is null, return head. (This line is optional and can be omitted without affecting the core functionality.)
Reverse the Linked List:
- Initialize cur as head, pre as null, and a temporary variable nxt.
- While cur is not null, do the following:
  - Store the next node in nxt.
  - Reverse the next pointer of cur to point to pre.
  - Update pre to cur.
  - Move cur to the next node (nxt).
Update head:
- After the loop, set head to pre, making the reversed list the new head.

Dry Run¶

Initialize the pointers

prev = null
curr = 2 -> 5 -> 8 -> 7 -> 3 -> null
nxt = null

Iteration 1:¶

Store the next node in nxt

nxt = curr.next; nxt = 5 -> 8 -> 7 -> 3 -> null

Reverse the next pointer of the current node

curr.next = prev

Update the previous and current pointers

prev = curr
curr = nxt
prev = 2 -> null
curr = 5 -> 8 -> 7 -> 3 -> null

Iteration 2:¶

Store the next node in nxt

nxt = curr.next; nxt = 8 -> 7 -> 3 -> null

Reverse the next pointer of the current node

curr.next = prev

Update the previous and current pointers

prev = curr
curr = nxt
prev = 5 -> 2 -> null
curr = 8 -> 7 -> 3 -> null

Iteration 3:¶

Store the next node in nxt

nxt = curr.next; nxt = 7 -> 3 -> null

Reverse the next pointer of the current node

curr.next = prev

Update the previous and current pointers

prev = curr
curr = nxt
prev = 8 -> 5 -> 2 -> null
curr = 7 -> 3 -> null

Iteration 4:¶

Store the next node in nxt

nxt = curr.next; nxt = 3->null

Reverse the next pointer of the current node

curr.next = prev

Update the previous and current pointers

prev = curr
curr = nxt
prev = 7 -> 8 -> 5 -> 2 -> null
curr = 3 -> null

Iteration 5:

Store the next node in nxt

nxt = curr.next; nxt = null

Reverse the next pointer of the current node

curr.next = prev

Update the previous and current pointers

prev = curr
curr = nxt
prev = 3 -> 7 -> 8 -> 5 -> 2 -> null
curr = null

The loop terminates because curr is now null

Final state of the linked list:

prev = 3 -> 7 -> 8 -> 5 -> 2 -> null
curr = null
The head of the linked list is now prev, which is the reversed linked list:

3 7 8 5 2

Question¶

Reverse the given Linked List.

Linked List : 5 -> 6 -> 7 -> 8 -> 9

Choices

5 -> 6 -> 7 -> 8 -> 9
5 <- 6 <- 7 <- 8 <- 9
9 -> 6 -> 7 -> 8 -> 5
5 <- 6 -> 7 <- 8 <- 9

Reverse the LinkedList Psuedo code and Time Complexity¶

Psuedocode¶

if (head == null)
  return head;

if (head.next == null)
  return head;

cur = head;
pre = null;

while (cur != null) {
  next = cur.next;
  cur.next = pre;
  pre = cur;
  cur = next;
}

head = pre;

TC & SC¶

Time complexity - O(N)
Space complexity - O(1)

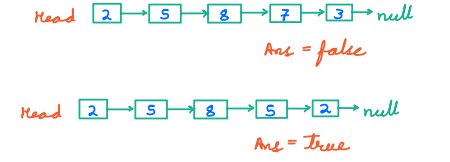
Problem 2 Check Palindrome¶

Given a Linked List, check if it is a palindrome.

Example:

maam, racecar, never, 121, 12321

Question¶

Check the Given linked list is Palindrome or not.

Linked List : Head -> 1 -> Null

Choices

YES
NO

Explanation:

Yes, The Given Linked List is an Palindrome, Because it reads the same in reverse order as well.

Warning

Please take some time to think about the solution approach on your own before reading further.....

Check Palindrome Solution¶

Solution 1 :

Create a copy of linked list. Reverse it and Compare

Complexity

Time Complexity - O(N)
Space Complexity - O(N).

Solution 2 :

Find middle element of linked list
Reverse second half of linked list
Compare first half and compare second half

Step wise solution:

Find length of linked list

n = 0
temp = Head
while(temp != null){
    n++
    temp = temp.next
}

Go to the middle element

// If n = 10(even), we'll reverse from 6^th node.
// If n = 9(odd), then also we'll reverse from 6^th node.(5^th node will be middle one that need not be compared with any node)

So, regardless of even/odd, we can skip (n + 1) / 2 nodes.

temp Head
(for i --> 1 to (n + 1) / 2){
    temp =temp.next
}
//temp middle

Now reverse the linked list from \(((n+1)/2 + 1)th\) node.
Compare both the linked list

T.C & S.C¶

Total time complexity for checking palindrome is O(N) and space complexity is O(N).