Linked List 2: Sorting and Detecting Loop¶
Question¶
What is the time complexity needed to delete a node from a linked list?
Choices
- O(1)
- O(log(N))
- O(N)
- O(N^2)
Explanation¶
To delete a node from the linked list we need to traverse till that node. In the worst case, the time-complexity would be O(N).
Question¶
What is the time complexity needed to insert a node as the head of a linked list?
Choices
- O(1)
- O(log(N))
- O(N)
- O(N\(^2\))
Explanation
No traversal is needed to reach the head node. Therefore the time complexity needed is constant i.e. O(1).
Question¶
What is the time complexity needed to delete the last node from a linked list?
Choices
- O(1)
- O(log(N))
- O(N)
- O(N\(^2\))
Explanation:
To delete the last node from the linked list we need to traverse till that node. In that case, the time-complexity would be O(N).
Question¶
Can we do Binary Search in a sorted Linked List?
Choices
- Yes
- No
Explanation:
Binary search relies on random access to elements, which is not possible in a linked list.
Problem 1 Find the middle element.¶
Given a Linked List, Find the middle element.
Examples
Following 0 based indexing: The middle node is the node having the index (n / 2), where n is the number of nodes.
Input: [1 -> 2 -> 3 -> 4 -> 5]
Output: [3]
Here 3 is the middle element
Input: [1 -> 2 -> 3 -> 4]
Output: [2]
There are two middle elements here: 2 and 3 respectively.
Warning
Please take some time to think about the solution approach on your own before reading further.....
Find the middle element Solution¶
Solution¶
- First, We will find the length of the linked-list.
- Now we will traverse half the length to find the middle node
Pseudocode¶
function findMiddle(head){
if head is null
return null
count = 0
current = head
while current is not null
count = count + 1
current = current.next
middleIndex = count / 2
current = head
for i = 0 to middleIndex - 1
current = current.next
return current
}
Complexity¶
Time Complexity: O(n * 2) = O(n)
Space Complexity: O(1)
Optimized Solution¶
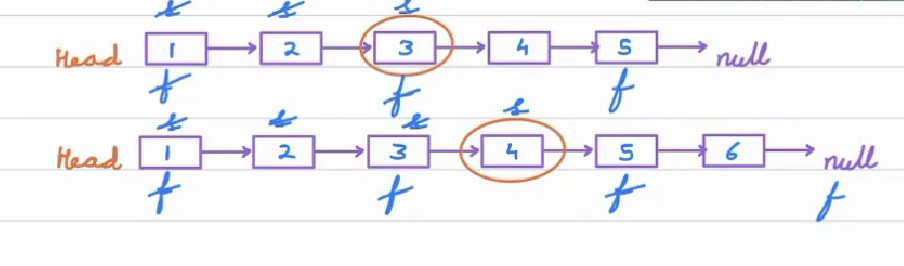
We can optimize the solution using the Two Pointers technique.
- Take two pointers initially pointing at the head of the Linked List and name them slowPointer and fastPointer respectively.
- The fastPointer will travel two nodes at a time, whereas the slowPointer will traverse a single node at a time
- When the fastPointer reaches the end node, the slowPointer must necessarily be pointing at the middle node
Pseudocode¶
function findMiddleTwoPointers(head){
if head is null
return null
slowPointer = head
fastPointer = head
while fastPointer is not null and fastPointer.next is not null
slowPointer = slowPointer.next
fastPointer = fastPointer.next.next
return slowPointer
}
Complexity¶
Time Complexity: O(n / 2) = O(n)
Space Complexity: O(1)
Problem 2 Merge two sorted Linked Lists¶
Given two sorted Linked Lists, Merge them into a single sorted linked list.
Example 1 :
Input: [1 -> 2 -> 8 -> 10], [3 -> 5 -> 9 -> 11]
Output: [1 -> 2 -> 3 -> 8 -> 9 -> 10 -> 11]
Example 2 :
Input: [1 -> 7 -> 8 -> 9], [2 -> 5 -> 10 -> 11]
Output: [1 -> 2 -> 5 -> 7 -> 8 -> 9 -> 11]
Question¶
Given two sorted Linked Lists, Merge them into a single sorted linked list.
Input: [2 -> 10 -> 11] [1 -> 5 -> 12 -> 15]
Choices
- [1 -> 2 -> 5 -> 10 -> 11 -> 12 -> 15]
- [2 -> 10 -> 11 -> 1 -> 5 -> 12 -> 15]
- [1 -> 5 -> 12 -> 15 -> 2 -> 10 -> 11]
- [1 -> 2 -> 10 -> 5 -> 12 -> 11 -> 15]
Warning
Please take some time to think about the solution approach on your own before reading further.....
Merge two sorted Linked Lists Solution¶
Solution¶
- Base Cases Handling: First of all, we need to take care of the Base cases: if either list is empty,we return the other list
- Determine Merged List's Head: The algorithm compares the first nodes of the two lists. The smaller node becomes the head of the merged list.
- Merge the Remaining Nodes:Merge the remaining nodes in such a way that whichever linked lists node is the smallest, we add it to the current list
- We continue doing this till the end of one of the linked lists is reached
- Finally we attach any remaining nodes from list1 or list2
- Returning the Result: We return the linked list
Pseudocode¶
function mergeSortedLists(list1, list2) {
if list1 is null
return list2
if list2 is null
return list1
mergedList = null
if list1.data <= list2.data
mergedList = list1
list1 = list1.next
else
mergedList = list2
list2 = list2.next
current = mergedList
while list1 is not null and list2 is not null
if list1.data <= list2.data
current.next = list1
list1 = list1.next
else
current.next = list2
list2 = list2.next
current = current.next
if list1 is not null
current.next = list1
if list2 is not null
current.next = list2
return mergedList
}
Complexity¶
Time Complexity: O(n + m)
Space Complexity: O(1)
Problem 3 Sort a Linked List¶
A Linked List is given, Sort the Linked list using merge sort.
Example
Input: [1 -> 2 -> 5 -> 4 -> 3]
Output: [1 -> 2 -> 3 -> 4 -> 5]
Input: [1 -> 4 -> 3 -> 2]
Output: [1 -> 2 -> 3 -> 4]
Solution¶
Base Case:
The function starts by checking if the head of the linked list is null or if it has only one element (i.e., head.next is null). These are the base cases for the recursion. If either of these conditions is met, it means that the list is already sorted (either empty or has only one element), so the function simply returns the head itself.
Find the Middle Node:
If the base case is not met, the function proceeds to sort the list. First, it calls the findMiddle function to find the middle node of the current list. This step is essential for dividing the list into two halves for sorting.
Split the List:
After finding the middle node (middle), the function creates a new pointer nextToMiddle to store the next node after the middle node. Then, it severs the connection between the middle node and the next node by setting middle.next to null. This effectively splits the list into two separate sublists: left, which starts from head and ends at middle, and right, which starts from nextToMiddle.
Recursively Sort Both Halves:
The function now recursively calls itself on both left and right sublists. This recursive step continues until each sublist reaches the base case (empty or one element). Each recursive call sorts its respective sublist.
Merge the Sorted Halves:
Once the recursive calls return and both left and right sublists are sorted, the function uses the mergeSortedLists function to merge these two sorted sublists into a single sorted list. This merging process combines the elements from left and right in ascending order.
Return the Sorted List:
Finally, the function returns the sortedList, which is the fully sorted linked list obtained by merging the sorted left and right sublists
Pseudocode¶
// Function to merge two sorted linked lists
function mergeSortedLists(list1, list2)
if list1 is null
return list2
if list2 is null
return list1
mergedList = null
if list1.data <= list2.data
mergedList = list1
mergedList.next = mergeSortedLists(list1.next, list2)
else
mergedList = list2
mergedList.next = mergeSortedLists(list1, list2.next)
return mergedList
function findMiddle(head)
if head is null or head.next is null
return head
slow = head
fast = head.next
while fast is not null and fast.next is not null
slow = slow.next
fast = fast.next.next
return slow
function mergeSort(head)
if head is null or head.next is null
return head
// Find the middle node
middle = findMiddle(head)
nextToMiddle = middle.next
middle.next = null
// Recursively sort both halves
left = mergeSort(head)
right = mergeSort(nextToMiddle)
// Merge the sorted halves
sortedList = mergeSortedLists(left, right)
return sortedList
Complexity¶
Time Complexity: O(Nlog(N))
Space Complexity: O(log(N))
Problem 4 Detect Cycle in a Linked List.¶
Given a Linked List, Find whether it contains a cycle.
Example 1
Input:
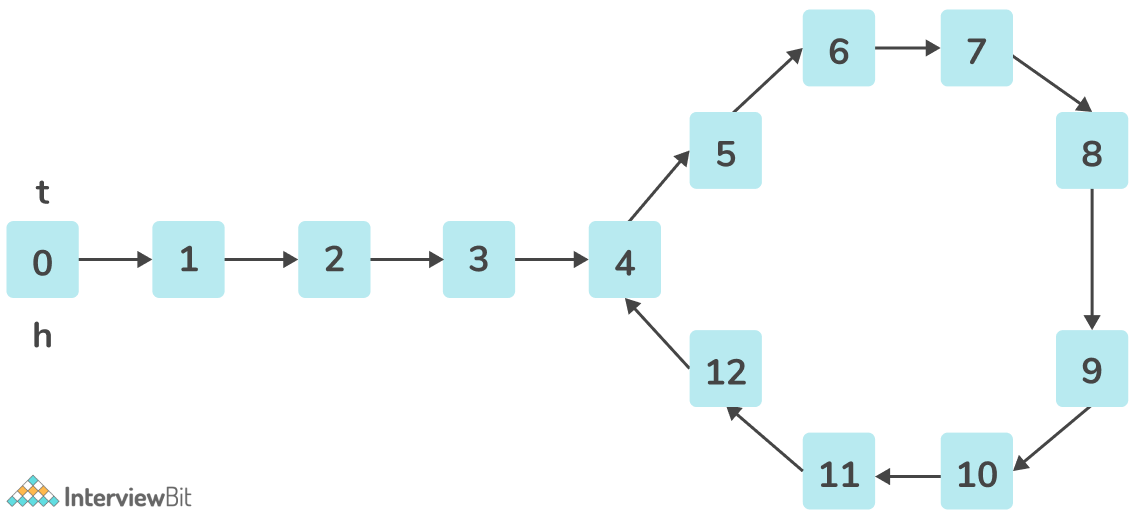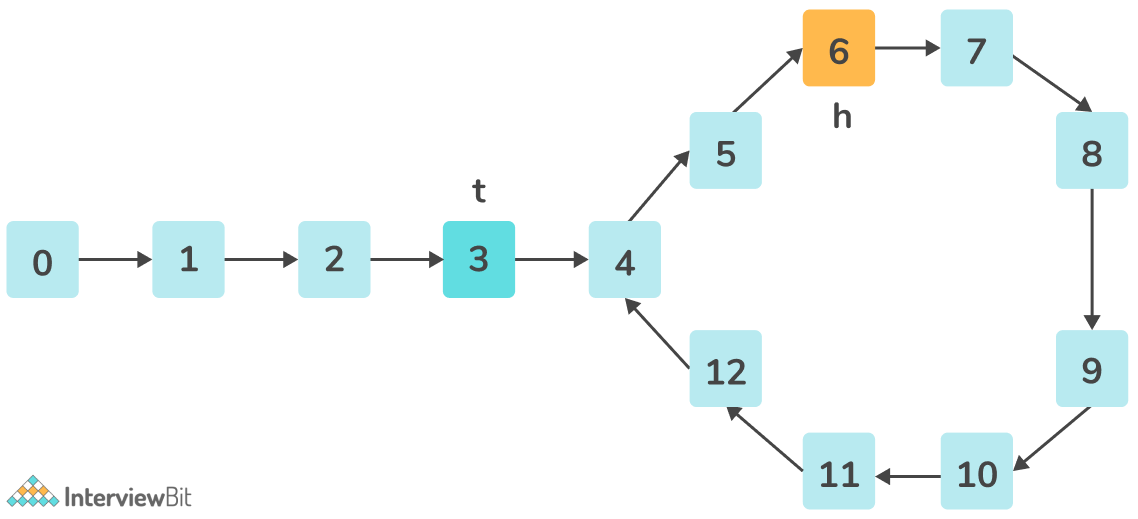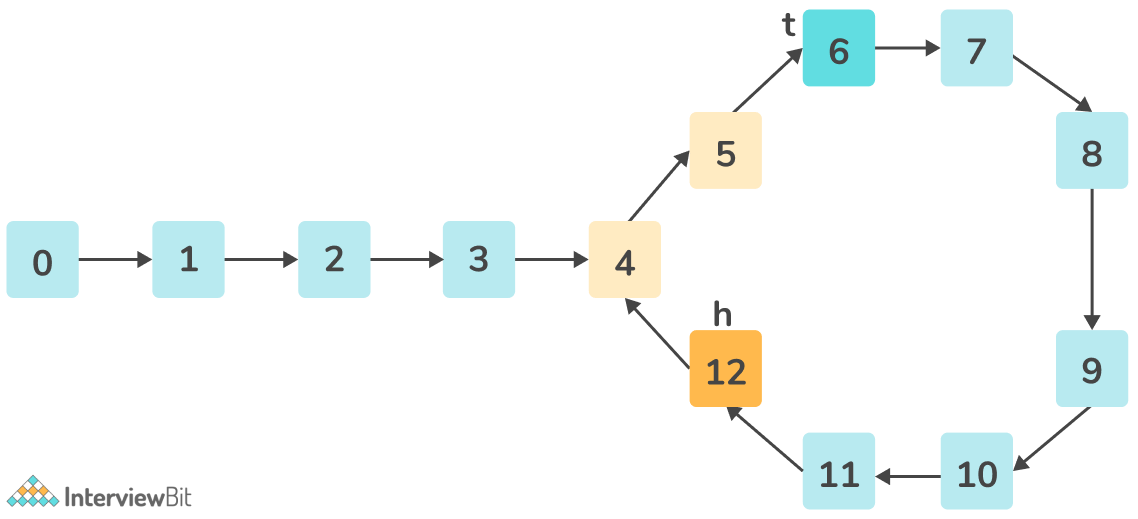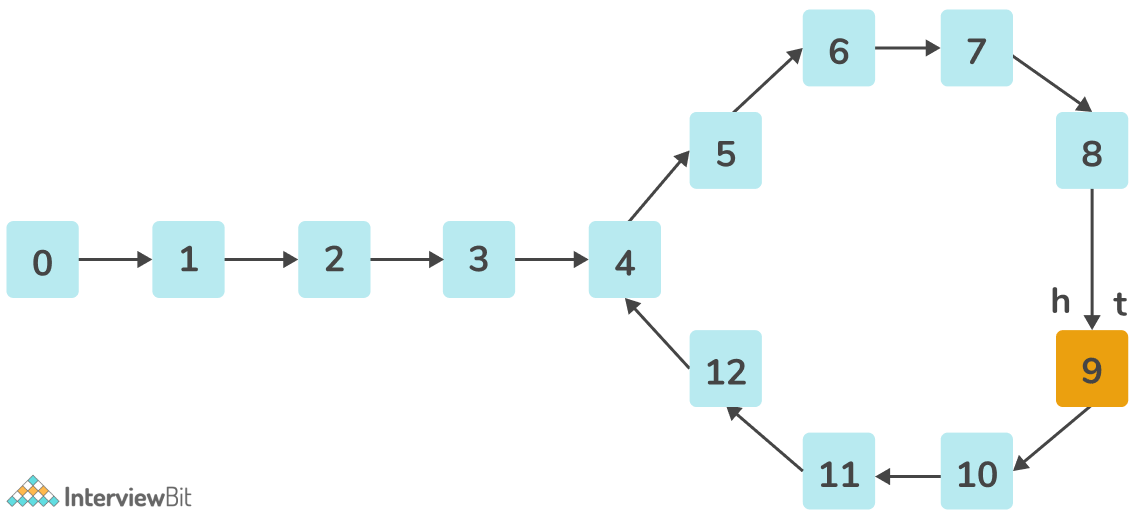
Output:
Yes
Example 2
Input:
Input: [1 -> 4 -> 3 -> 2 -> 11 -> 45 -> 99]
Output:
No
Detect Cycle in a Linked List Solution¶
Solution¶
-
Initialization:
Start with two pointers, slow and fast, both pointing to the head of the linked list. -
Traversal:
In each iteration, the slow pointer advances by one step, while the fast pointer advances by two steps. This mimics the tortoise and hare analogy. If there is a cycle, these two pointers will eventually meet at some point within the cycle. -
Cycle Detection:
While traversing, if the slow pointer becomes equal to the fast pointer, this indicates that the linked list contains a cycle. This is because the fast pointer "catches up" to the slow pointer within the cycle. -
No Cycle Check:
If the fast pointer reaches the end of the linked list and becomes null or if the fast pointer's next becomes nullp, this means there is no cycle in the linked list. -
Cycle Detected:
If the slow and fast pointers meet, it implies that the linked list contains a cycle. The function returns true.
Pseudo Code¶
function hasCycle(head)
if head is null or head.next is null
return false // No cycle in an empty or single-node list
slow = head
fast = head.next
while fast is not null and fast.next is not null
if slow is the same as fast
return true // Cycle detected
slow = slow.next
fast = fast.next.next
return false // No cycle detected
Complexity¶
Time Complexity: O(N)
Space Complexity: O(1)
Problem 5 Find the starting point¶
Given a Linked List which contains a cycle , Find the start point of the cycle.
Example
Input:
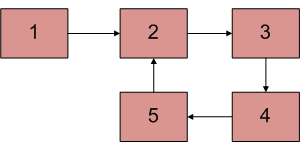
Output:
5
Find the starting point Solution¶
Warning
Please take some time to think about the solution approach on your own before reading further.....
Solution¶
-
Initialization:
Similar to cycle detection, start with two pointers, slow and fast, both pointing to the head of the linked list. -
Cycle Detection:
In each iteration, move the slow pointer by one step and the fast pointer by two steps. If a cycle exists, they will eventually meet within the cycle. -
Meeting Point:
If a cycle is detected (slow meets fast), set a flag hasCycle to true. -
Start Point Identification:
Reset the slow pointer to the head of the list while keeping the fast pointer at the meeting point. Advance both pointers by one step in each iteration. They will eventually meet at the start point of the cycle. -
Returning the Result:
Once the slow and fast pointers meet again, it implies that the linked list has a cycle, and the meeting point is the start of the cycle. Return this pointer.
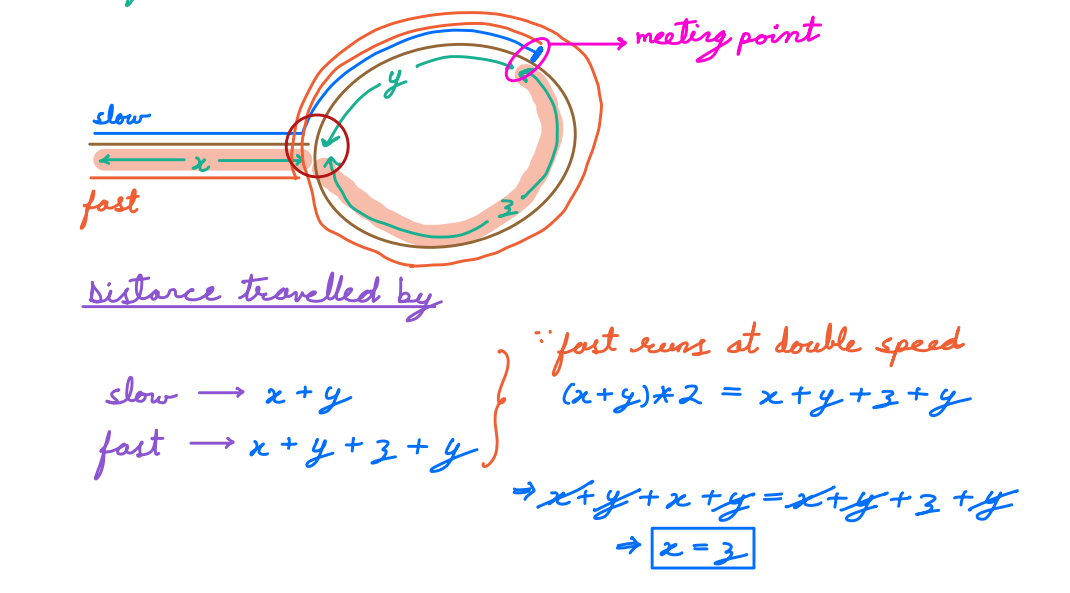
Assume that the length from the head to the first node of cycle is x and the distance from the first node of cycle to the meeting point is y. Also the length from the meeting point to the first node is z.
Now, speed of the fast pointer is twice the slow pointer
2(x + y) = x + y + z + y
x = z
- No Cycle Check: If the fast pointer reaches the end of the linked list (i.e., becomes nullptr) or if the fast pointer's next becomes nullptr, there is no cycle. In such cases, return nullptr.
This approach ensures that you can find the start point of the cycle using the Floyd's Tortoise and Hare algorithm with a slightly modified process.
Pseudo Code¶
function detectCycleStart(head)
if head is null or head.next is null
return null // No cycle in an empty or single-node list
slow = head
fast = head
hasCycle = false
while fast is not null and fast.next is not null
slow = slow.next
fast = fast.next.next
if slow is the same as fast
hasCycle = true
break
if not hasCycle
return null // No cycle detected
slow = head
while slow is not the same as fast
slow = slow.next
fast = fast.next
return slow // Return the start point of the cycle
Complexity¶
Time Complexity: O(N)
Space Complexity: O(1)
