Linked List 3: Problems & Doubly Linked List¶

What is doubly linked list¶

A doubly linked list is a type of data structure used in computer science and programming to store and organize a collection of elements, such as nodes. It is similar to a singly linked list but with an additional feature: each node in a doubly linked list contains pointers or references to both the next and the previous nodes in the list.

Example

Correlation with Singly Linked List¶

The main difference between singly linked lists and doubly linked lists lies in the bidirectional traversal capability of the latter, which comes at the cost of increased memory usage. The choice between them depends on the specific requirements of the problem we're solving and the operations we need to perform on the list

Note-1: Sometimes the previous pointer is called the left pointer and the next pointer is called the right pointer.
Note-2: The previous pointer of the first node always points to null and the next pointer of the last node also points to null in the doubly linked list.

Question¶

prev Pointer of Head of Doubly LinkedLIst points to:

Choices

Next to Head Node
Null pointer
Tail
Depends

Problem 1 Insert node in a doubly linked list¶

A doubly linked list is given. A node is to be inserted with data X at position K. The range of K is between 0 and N where N is the length of the doubly Linked list.

Example

Question¶

In a doubly linked list, the number of pointers affected for an insertion operation between two nodes will be?

Choices

For insertions in the middle of the list four pointer assignments take place.

Insert node in a doubly linked list Solution¶

Solution¶

A naive approach to insert a node with data X at position K in a doubly linked list of length N would involve traversing the list from the beginning until position K is reached, and then updating the pointers of the adjacent nodes to include the new node. This approach takes O(K) time complexity in the worst case.

Our Approach¶

Let us now move on to the below approach:

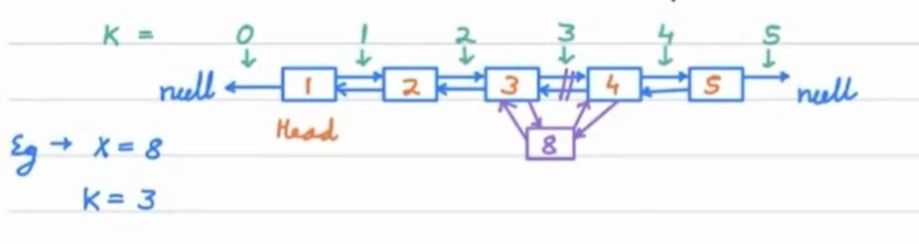
Suppose given data are X = 8 and K = 3 and the provided linked list contains the nodes 1, 2, 3, 4, 5. Now, describe the overall approach in a step-wise manner.

The very first thing that can be done is to create a node with data X whose previous and next pointers are pointing toward null currently.
Next, we need to check if our linked list is empty or not. In the case of an empty linked list head pointer points towards null. So, if the head pointer is pointing towards null, we can simply return a new node with data X.
The next thing that we need to take care of is if the value of K is zero. In this case, we need to add a new node with data X pointed by the head pointer. we also need to update the head pointer and the next pointer of the newly created node.
Now that we have covered the two base cases, we can simply add the node by making K - 1 jumps from the head pointer. For this, we can create a temporary node that is currently pointing toward the head, and we will traverse the K - 1 nodes to reach the position where we want to add the new node.
The last and most important thing that we need to do here is to update the next and previous pointers of K - 1 and K + 1 nodes.

Let us now see the pseudo code of our approach.

Pseudocode¶

xn = new Node(x) // xn.next = xn.pre = null

// Empty List
if (head == null)
  return xn

// Update head
if (k == 0) {
  xn.next = head
  head.pre = xn
  head = xn
  return head
}

temp = head
for i = 1 to(k - 1)
temp = temp.next

xn.next = temp.next
xn.pre = temp
if (temp.next != null)
  temp.next.pre = xn
temp.next = xn
return head

Note: we should also check if our current position of insertion is the last node or not. In the case of the last node, the next pointer is pointing toward the null. So, we have to make it point to the current node.

Time and Space Complexity¶

Time Complexity: O(N), since we traverse the linked list only once.
Space Complexity: O(1) as we are not using any extra list.

Problem 2 Delete the first occurrence of a node from the doubly linked list¶

We have been given a doubly linked list of length N, we have to delete the first occurrence of data X from the given doubly linked list. If element X is not present, don't do anything.

Example

Delete the first occurrence Solution¶

Solution¶

A naive approach to solving this problem would be to start from the beginning of the doubly linked list and traverse it node by node. If the data of a node matches the given element, X, then remove that node by updating the next and previous pointers of the adjacent nodes to bypass the node to be deleted.

Our Approach¶

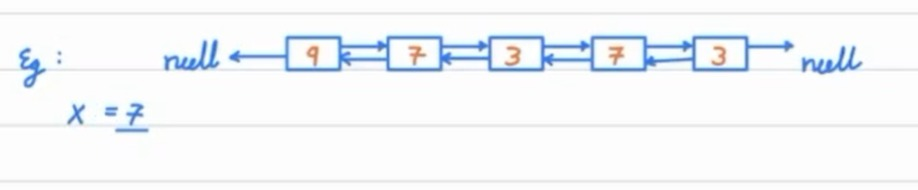
Suppose we have a DLL having nodes 9, 7, 3, 7, and 3, and we have to delete node 7. Let's break it into smaller steps:

The simple thing that we need to do in this problem is to grab the previous node and the next node of node X.
Then make the next pointer of the previous node point to the next node and make the previous pointer of the next node point to the previous node.
Now, move on to corner cases. The first corner case is when the head pointer is pointing to null. In this case, we simply need to return null as we cannot delete anything.
Now let's move on to the normal case and search for our next node. For searching we just need to create a temporary nod that is pointing to the head.
Now, we will traverse the entire list using temporary nodes and check if the current node's value is the same as the X's value.
If the value is found, we just need to stop searching and delete the node.

After traversal, we can have three situations:

If the temp pointer is pointing to null, this means that we have not found our node. So, we can simply return the head pointer.
If the previous pointer of the temporary node is pointing to null, then this means that our desired node is the first node. So, we need to delete the head pointer and simply return null. This will work the same if the next pointer of temp is null.
If both the above corner cases are not encountered, then we can simply delete the current node that is pointed by temp.

Let us now see the pseudo code of our approach.

Pseudocode¶

temp = head

// Searching
while (temp != null) {
  if (temp.data == X)
    break
  temp = temp.next
}

// No update
if (temp == null) {
  return head
}

// Single node
if (temp.pre == null and temp.next == null) {
  return null
} else if (temp.pre == null) // delete head
{
  temp.next.pre = null
  head = temp.next
} else if (temp.next == null) {
  temp.pre.next = null
} else {
  temp.pre.next = temp.next
  temp.next.pre = temp.pre
}
return head

Time and Space Complexity¶

Time Complexity: O(N), since we traverse the linked list only once.
Space Complexity: O(1) as we are not using any extra list.

Problem 3 LRU¶

We have been given a running stream of integers and the fixed memory size of M, we have to maintain the most recent M elements. In case the current memory is full, we have to delete the least recent element and insert the current data into the memory (as the most recent item).

Example

This question is closely related to the concept of an LRU (Least Recently Used) cache memory. An LRU cache is a data structure that maintains a fixed-size memory and stores the most recently accessed items. When the cache is full and a new item needs to be inserted, the least recently used item is evicted to make space for the new item.

Question¶

What is the behavior of an LRU cache memory when a new item is inserted and the cache is already full?

Choices

The new item is added to the cache, and the least recently used item is removed from the cache.
The new item is not added to the cache, and the least recently used item is not removed from the cache.
The new item is added to the cache, and the least recently used item is updated to be the most recently used item.
The new item is not added to the cache, and the most recently used item is removed from the cache.

In an LRU cache, the least recently used item is always the one that is removed when the cache is full and a new item needs to be inserted. This ensures that the most recently accessed items are always prioritized and kept in the cache.

LRU Solution¶

Warning

Please take some time to think about the solution approach on your own before reading further.....

Solution¶

Suppose we have several data to be inserted and the memory size is M = 5. So, we will take data one by one and insert it into the memory. As soon as the memory gets full, we have to delete the oldest data. In case a number comes and the same number is present in the memory pool, it will not be deleted but it will be considered as the most recent element.

A decision tree or flow chart can also be created for the problem.

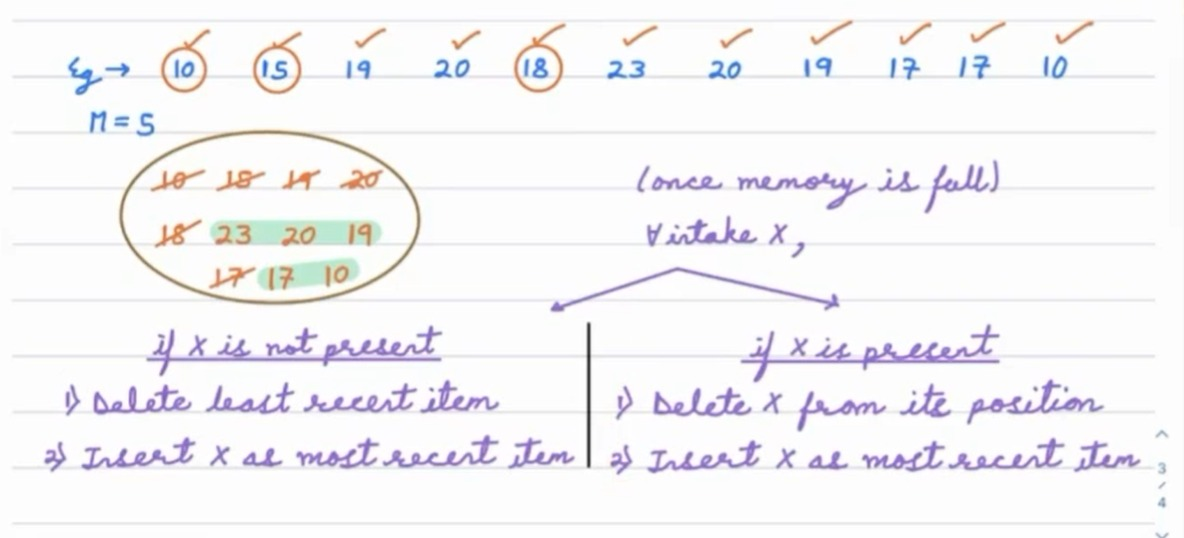
There can be two cases when a new number is to be inserted.

If the current number is not present in the memory pool. In this case, we can simply delete the oldest number (i.e. deleting the head node).
If the current number is present in the memory pool. In this case, we have to maintain the number X, as well as its position. So we can use a data structure called HashMap.

Let us now see the pseudo code of our approach.

Our Approach¶

So, the conclusion is that we have to use a Doubly Linked List or a hashmap for the solution to this problem. Let now move on to the Coding / Solution part:

Create a HashMap. Storing the value X, and the node of X.
Check if the HashMap contains X and the size of memory is not full, then we can simply put a new number at the last position. In this case, we also need to tackle the corner cases of the problem - Deletion of a new node from the doubly linked list.
The last case is when the number X is not present in the memory pool. Here, if the memory is full, we have to delete the oldest number i.e. the head node of the DLL( that we covered in the previous question). If the memory is not full we need to insert a new node into DLL at last.

Important Concept¶

There is an important concept in the Doubly linked list that is shallow copying and deep copying.

In a doubly linked list, the concept related to shallow copying and deep copying is about how references (pointers) to nodes are managed during copying: "Shallow copying" involves copying the structure of the list, including the references, while "deep copying" involves creating new nodes and copying their content to have an independent copy of the original list.

Pseudocode¶

// Take a hashmap (hm)
HashMap < x, node of x > hm;

if (h.containsKey(X)) {
  // Delete x from its position
  xn = hm.get(x)
  head = deleteNode(xn, head)
  // insert as as node
  tail.next = xn
  xn.pre = tail
  tail = xn
} else // Not present
{
  // full memory
  if (hm.size() == M) {
    hm.remove(head.data)
    deleteNode(head)
  }
  xn = new Node(x)
  hm.put(x, xn)
  if (hm.size() > 1) {
    // Insert as last node
    tail.next = xn
    xn.pre = tail
    tail = xn
  } else {
    head = tail = xn
  }
}

Time and Space Complexity¶

Time Complexity: O(N), since we traverse the linked list only once.
Space Complexity: O(1) since we are not using any additional list.

Problem 4 Deep copy of a doubly linked list¶

we have to create a deep copy of the Doubly Linked list with random pointers. Here there is no certain next and previous pointer, a node can point to some other node.

Example

Deep Copy Solution¶

Solution¶

A naive approach to creating a deep copy of a doubly linked list with random pointers could involve iteratively traversing the original list, creating new nodes with the same data and random pointers, and then using additional passes to update the random pointers to point to the corresponding new nodes in the copied list.

Our Approach¶

In a node, we have two pointers. The first one is the next pointer and the second one is a random pointer.
Our goal is to populate the Doubly Linked list using the next and random pointer. For this, we will be using the concept of deep copying in this.
Now, since we don't have the previous and next pointer as of the Doubly Linked list, we can use a HashMap to map the original nodes.
So, we will be creating the HashMap containing two things one is an old node and another is a new node but there is a small problem in this approach, we are using extra space here. As we only want the original mapping, we can solve this with constant space.

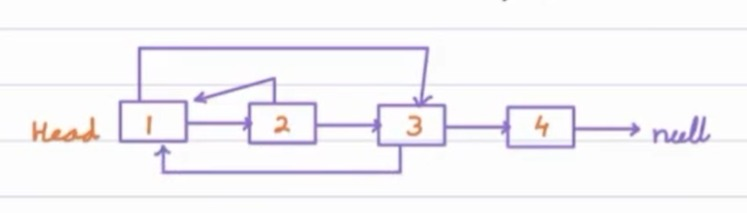
A systematic approach can be:

we will create a copy of each node calling it node_1 and making it pointed by the first node.
After this, we will make it point to the second node. So we are pushing a node between two nodes. > Note: Here, we can teach that this problem can be summarized as pushing a copy of a node between two nodes and then changing the random pointer.
Now, the problem becomes sorted as we only must copy a node and insert it in the middle of its previous and next node.
Finally, we will be shuffling the random pointer. For this, we will be using an extra node X, and X will be traversing until the last node of the list.

Pseudocode¶

// Populate random pointers
x = head
while (x != null) {
  y = x.next
  y.random = x.random.next
  x = x.next.next
}

// Separate two
h = head.next
x = head
while (x != null) {
  y = x.next
  x.next = x.next.next
  if (y.next != null) {
    y.next = y.next.next
  }
  x = x.next
}

return h

Time and Space Complexity¶

Time Complexity: O(N), as we are creating a deep copy of the doubly linked list with random pointers.
Space Complexity:O(N). In the case of deleting the first node, the time complexity remains O(1) as long as the deletion operation itself is O(1).

Question¶

What is the time complexity of creating a deep copy of a Doubly Linked List consists of N nodes with random pointers using extra space?

Choices

O(N)
O(N * N)
O(1)
O(log(N))