Maths 2: Combinatorics Basic¶

Addition and Multiplication Rule Example 1¶

Example - 1¶

Given 10 girls and 7 boys, How many different pairs can be formed?

Note: pair = 1 boy + 1 girl

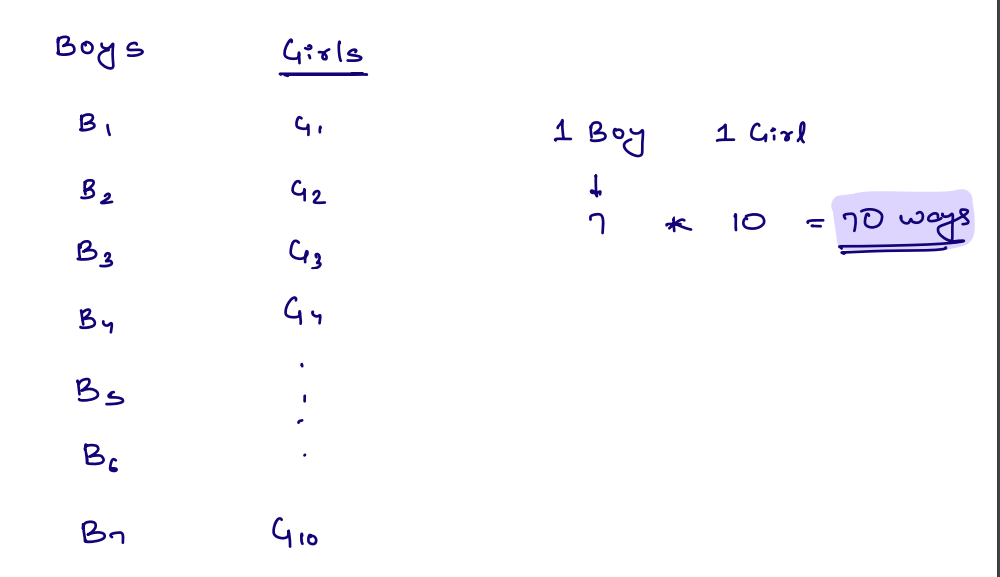
Since each pair consists of one boy and one girl, you can pair each of the 7 boys with any of the 10 girls. This results in a total of 7 boys × 10 girls = 70 different pairs that can be formed.

Addition and Multiplication Rule Example 2¶

Example - 2¶

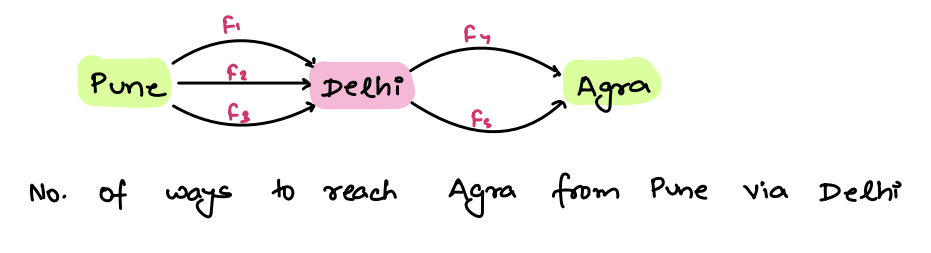
Approach:

To reach Agra via Delhi from Pune, you can combine the ways to get from Pune to Delhi (3 ways) with the ways to get from Delhi to Agra (2 ways).

So, the total number of ways to reach Agra via Delhi from Pune is:

3 ways (Pune to Delhi) * 2 ways (Delhi to Agra) = 6 ways.

Question¶

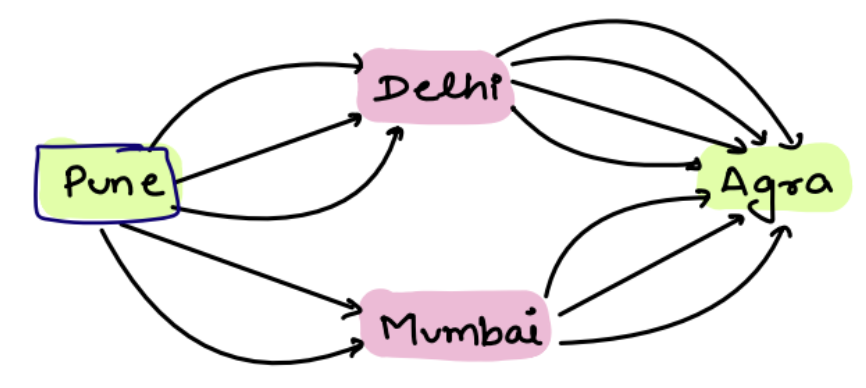
No. of ways of reaching Agra from Pune ?

Choices¶

72
12
18
20

To go to Pune to delhi , there are 3 ways. And do go from delhi to agra there are 4 ways. From pune to Mumbai there are 2 ways, from Mumbai to agra there are 3 ways.

To calculate the number of ways to reach Agra from Pune through different routes, you need to consider the combination of routes from Pune to Delhi and from Delhi to Agra, as well as the routes from Pune to Mumbai and from Mumbai to Agra. Then, you can add these possibilities together.

From Pune to Delhi, there are 3 ways.
From Delhi to Agra, there are 4 ways.

From Pune to Mumbai, there are 2 ways.
From Mumbai to Agra, there are 3 ways.

So, to find the total number of ways to reach Agra from Pune via these routes, you add the possibilities:

(3 ways from Pune to Delhi * 4 ways from Delhi to Agra) + (2 ways from Pune to Mumbai * 3 ways from Mumbai to Agra) = \((3 * 4) + (2 * 3) = 12 + 6 = 18\) ways.

There are 18 different ways to reach Agra from Pune through these routes.

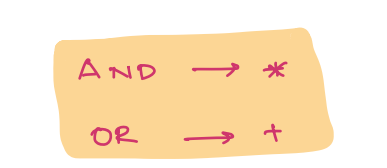
(Multiplication) = AND: Used when counting possibilities that occur together in sequence.
(Addition) = OR: Used when counting possibilities that occur in separate ways.

Permutation¶

Explanation¶

Permutation is defined as the arrangements of objects. In permutation, order matters. To simplify (i, j) != (j, i)

Example - 1¶

Given 3 distinct characters, in how many ways can we arrange them?

Approach:

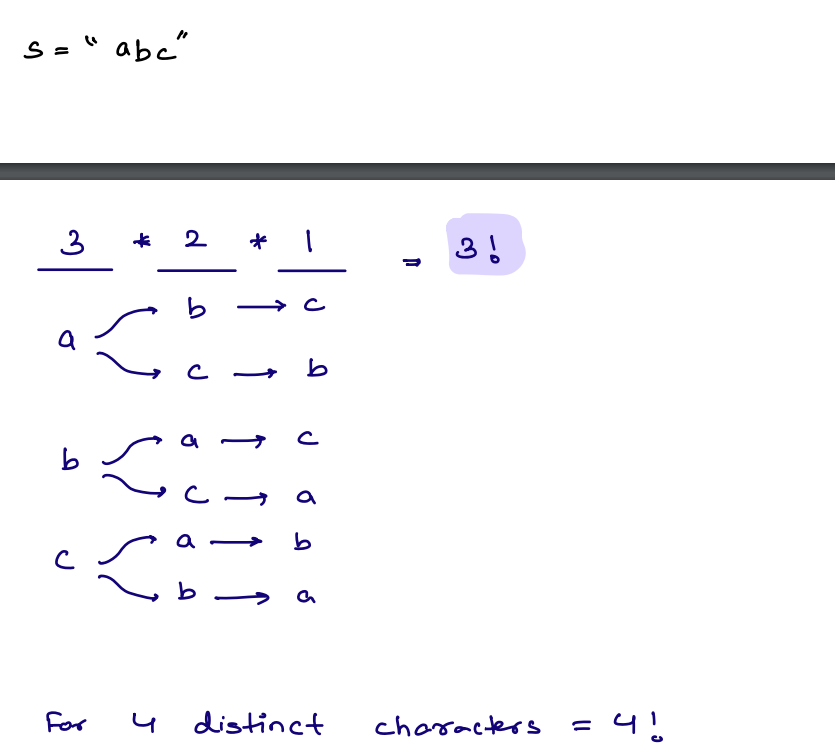
Question¶

In how many ways n distinct characters can be arranged?

Choices

N * (N + 1) / 2
N! (N Factorial)
N ^ 2
N

Explanation:¶

N distinct characters can be arranged in n! (n factorial) ways. This means that for each distinct character you have, you can multiply the total number of arrangements by the count of characters. Here's the formula:

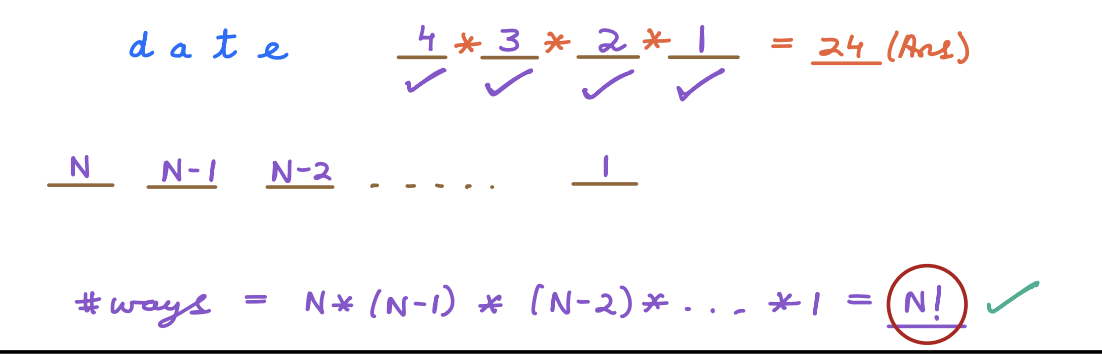
nPr Formulae¶

Example - 2¶

Given N distinct characters, in how many ways you can arrange R out of N distinct chracters?

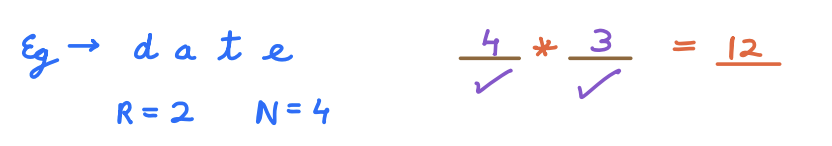
Approach:

When arranging 2 distinct characters from a set of 4, and order matters (e.g., AB and BA are considered different arrangements), the number of ways is indeed \(4 * 3 = 12\) ways.

When arranging R characters out of N distinct characters:

For the first position, you have N choices
For the second position, since you've used one character, you have N-1 choices.
For the third position, you have N-2 choices, and so on.

This continues until the R-th position, for which you have \(N-(R-1)\) choices.

Thus, the total number of ways to arrange R characters out of N distinct characters is N ∗ (N − 1) ∗ (N − 2) ∗ ... ∗ (N − (R − 1)).

Here:

n is the total number of distinct characters.
r is the number of characters you want to arrange.
nPr represents the permutations of n items taken r at a time.

Combination¶

Explanation¶

Combination is defined as the number of ways to select something.

Note: In combination, order of selection does not matter. To simplify (i, j) = (j, i)

Example - 1¶

Given 4 players, count the number of ways of selecting 3 players.

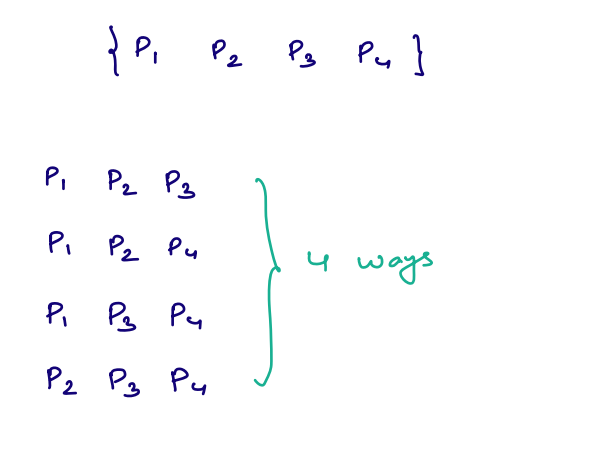
Example - 2¶

Given 4 players, write the number of ways to arrange players in 3 slots

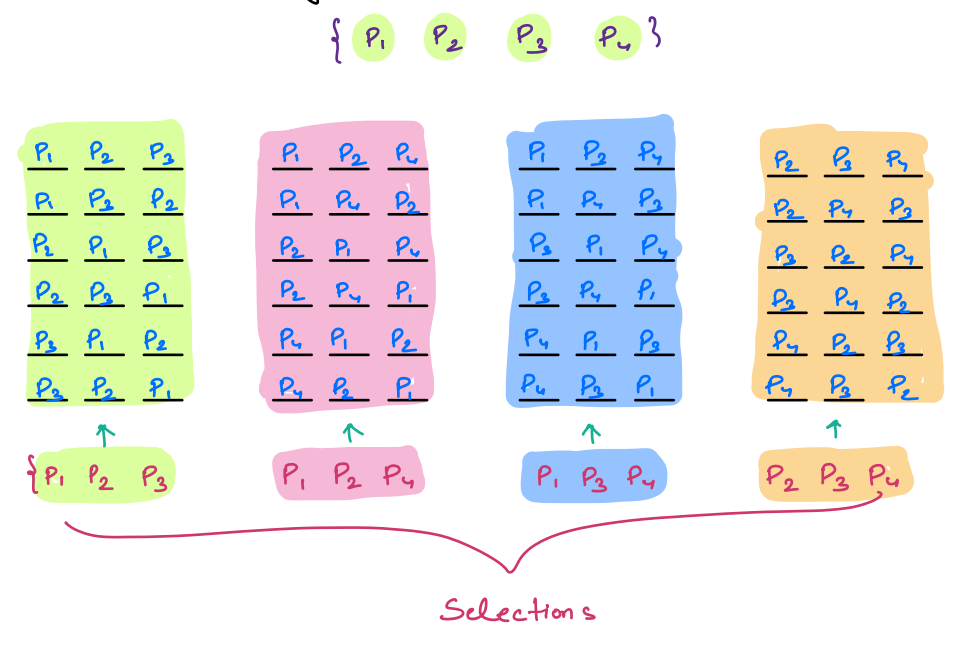
Number of Selections (x): You are selecting 3 players out of 4, which is represented as 4C3, and it equals 4.
Number of Arrangements in Each Selection (6): There are 3! (3 factorial) ways to arrange 3 players within 3 slots, which is 6.
Total Number of Arrangements: Multiply the number of selections by the number of arrangements in each selection:

Number of Selections * Number of Arrangements in Each Selection = \(4 * 6 = 24\)

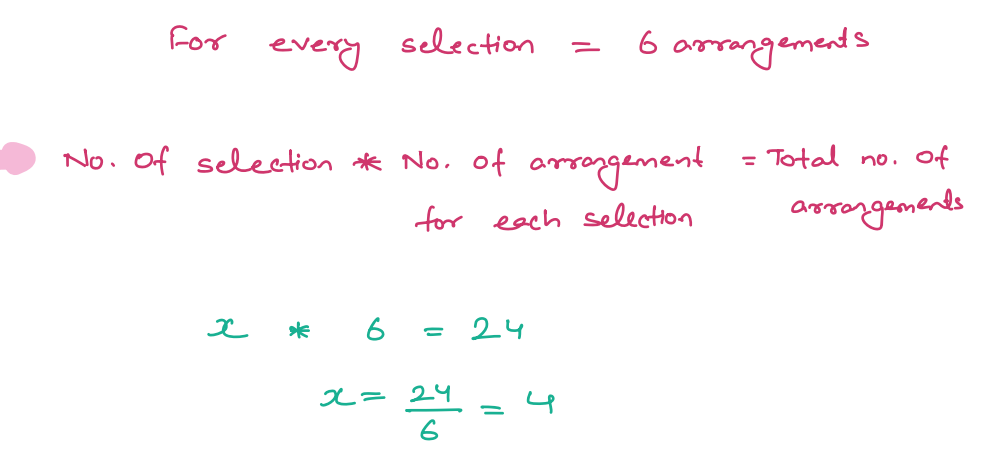
nCr Formulae¶

Example - 3¶

Given n distinct elements, in how many ways we can select r elements s.t 0 <= r <= n

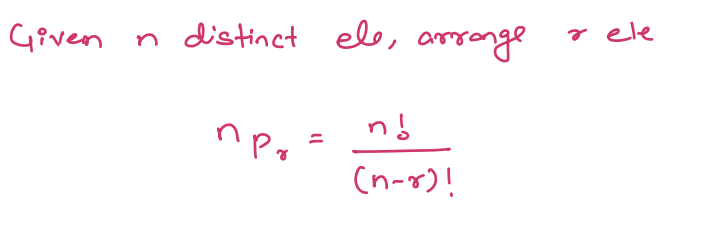
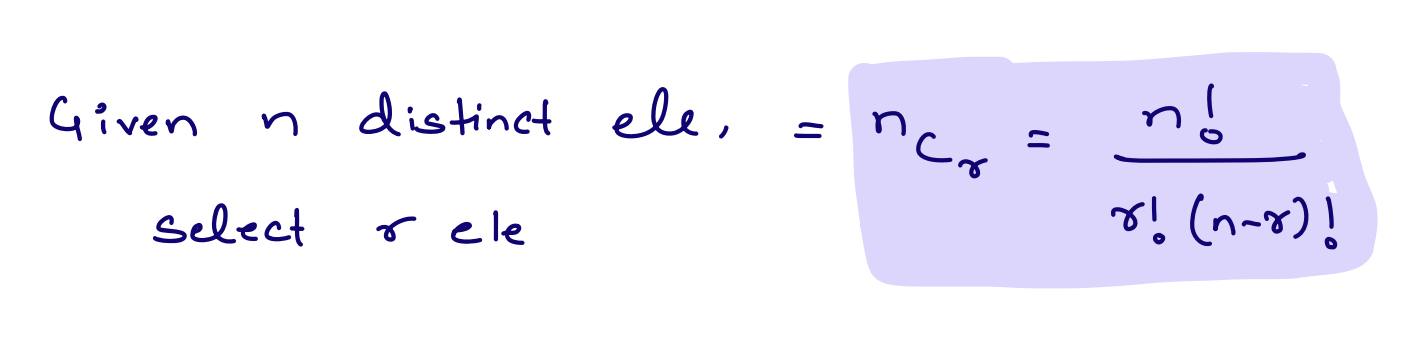
Properties of Combination¶

Property - 1¶

The number of ways of selecting 0 items from N items, i.e. number of ways to not select anything, will always be 1.

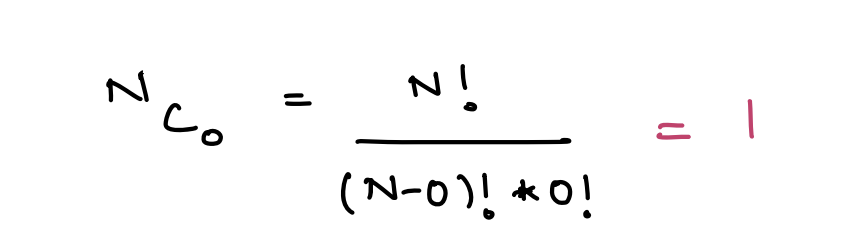
Property - 2¶

The number of ways of selecting n items from n, i.e. number of ways to select everything will also be 1.

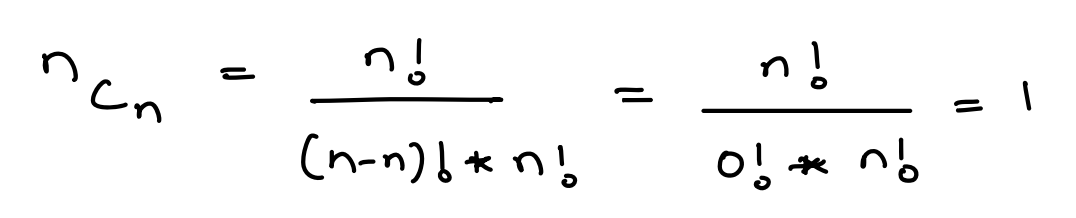
Property - 3¶

Number of ways of selecting (n-r) items from n:

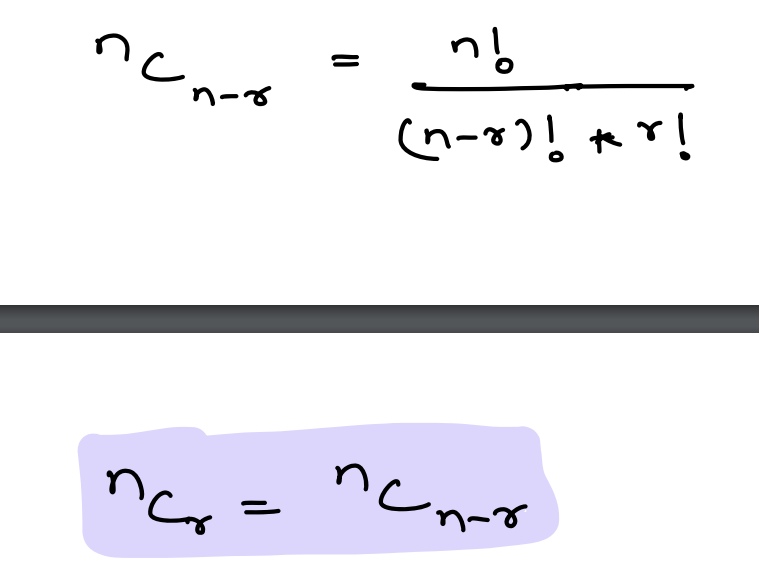
Special Property¶

Property - 4¶

Given n distinct elements, select r items:

For each elements, we have 2 options, either to select or not select:

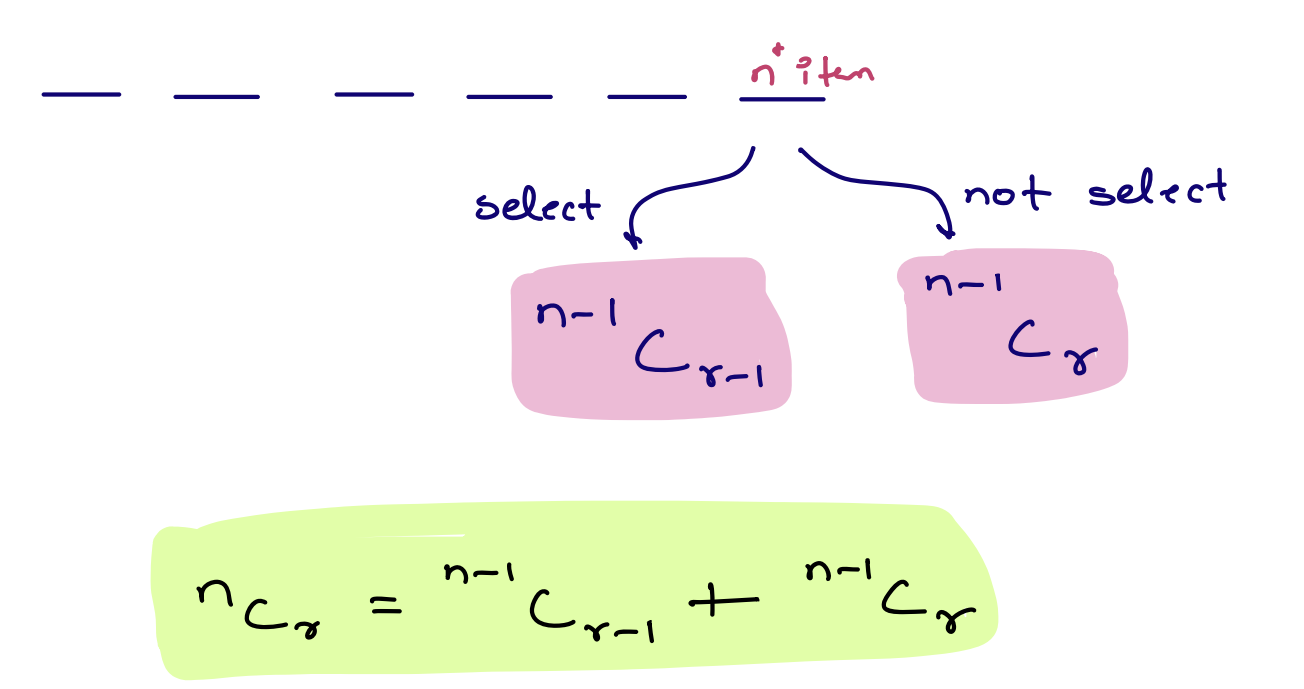
Select Case:

When you choose to "select" an element from the available n distinct elements, it means that you are including that specific element as one of the r items you want to pick. In this case:

You decrease the number of items you need to select by 1, so it becomes r - 1.
You decrease the total number of available elements by 1, as you've already chosen one element, so it becomes n - 1.
You continue the selection process, considering the reduced values of r and n.

Reject Case:

When you choose to "reject" an element, it means that you are not including that particular element as part of your selection. In this case:

You keep the number of items you need to select the same, which remains as r.
You decrease the total number of available elements by 1, as you've decided not to choose one element, so it becomes n - 1.
You continue the selection process with the same value of r and the reduced value of n.

Problem 1 Pascal Triangle¶

Generate Pascal's triangle for given value of n.

Example

Pascal Triangle for n = 4 is given below

Warning

Please take some time to think about the solution approach on your own before reading further.....

Brute Force: For each and every value, calculate the factorial and print it.

c[i][j] represents the element in the i-th and j-th column. Each element is the sum of the two numbers directly above it from the previous row. In combinatorial terms, c[i][j] indicates the number of ways to choose j items from a set of i items without repetition and without order.

But as we know that, factorial grows very fast as the number increases, hence this approach won't work properly.

Optimized Approach¶

Pascal's Triangle elements are calculated using c[i][j] = c[i - 1][j] + c[i - 1][j - 1], summing elements from the row above.
Start with c[0][0] = 1, forming the foundation of the triangle.
Calculate rows iteratively using the relation, reusing previous row values to minimize redundant calculations.
Utilize only two rows (previous and current) to calculate and update elements, saving memory.
Print each row's elements to see Pascal's Triangle emerge from the calculated values.

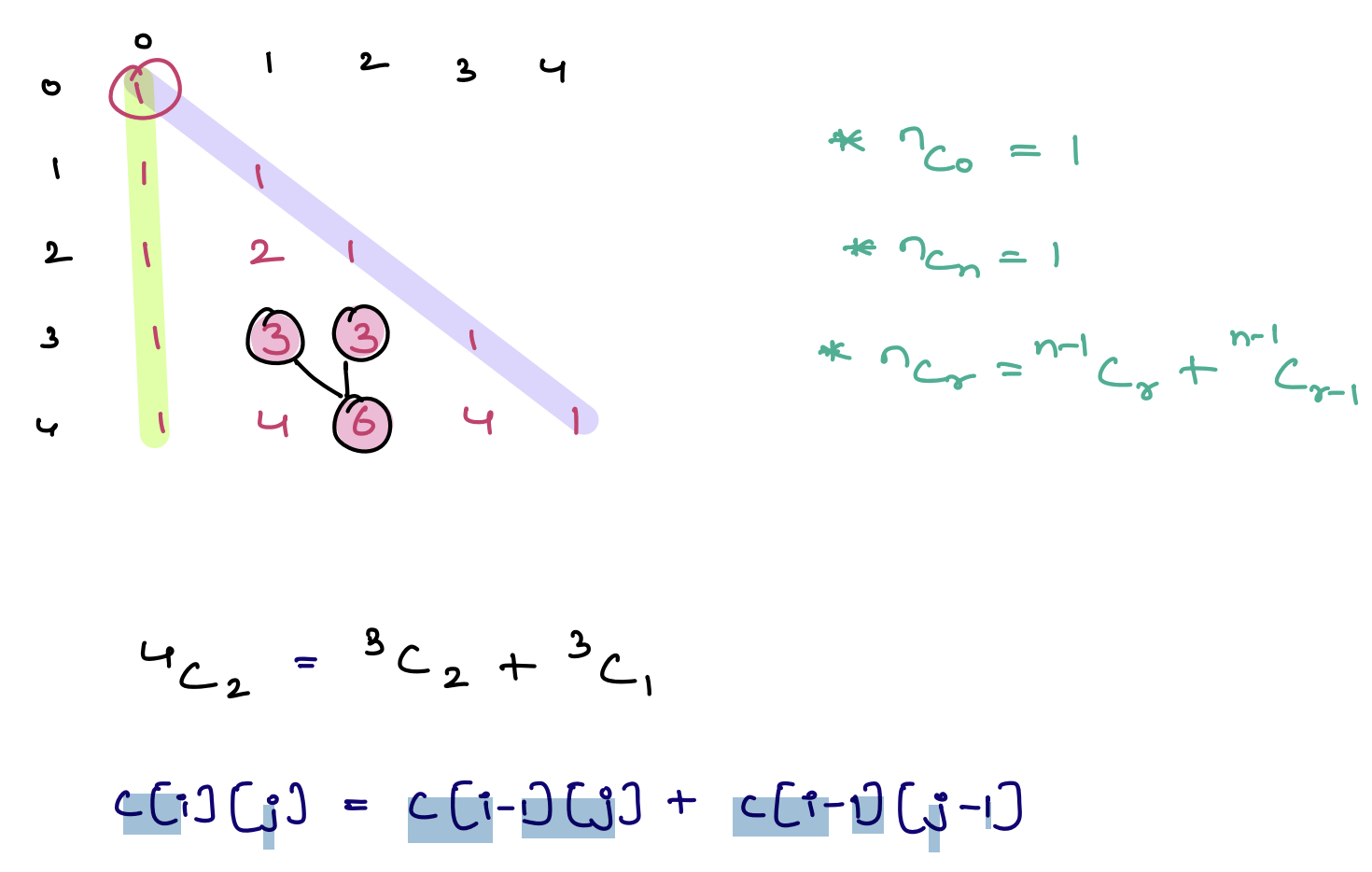
Pseudo Code¶

void pascalsTriangle(int n) {
    nCr[n][n] = {0};
    for (int i = 0; i < n; i++) {
        nCr[i][0] = 1;
        nCr[i][i] = 1;
        for (int j = 1; j < i; j++) {
            nCr[i][j] = nCr[i-1][j] + nCr[i-1][j-1];
            // If mentioned in the question to take % M then:
            // nCr[i][j] = (nCr[i-1][j] + nCr[i-1][j-1]) % M;
        }
        return nCr;
    }
}

Complexity¶

Time Complexity: \(O(N^2)\)
Space Complexity: \(O(N^2)\)

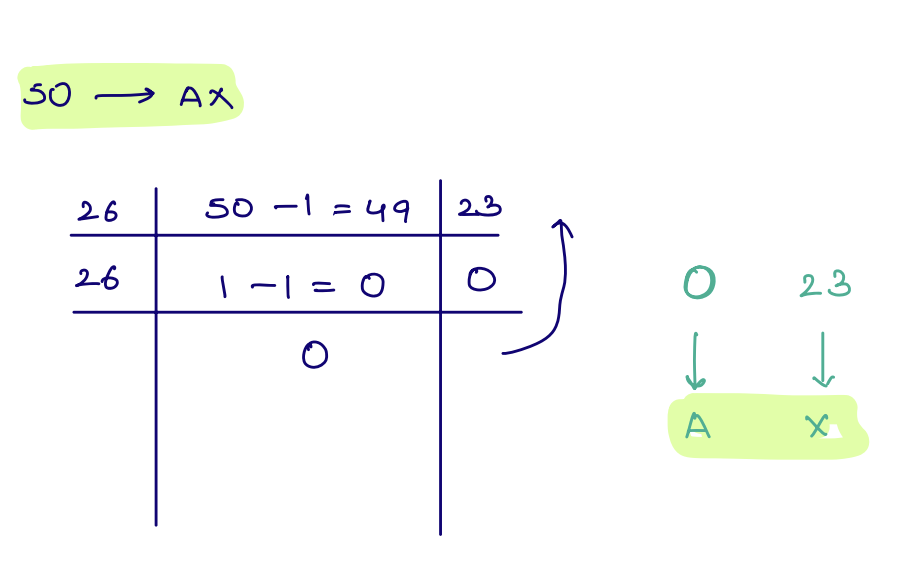
Problem 2 Finding N-th column title¶

Find the n-th column title, the columns are titled as A, B, C... and after Z, it is AA, AB, AC... and so on. Given the column number, find the title of the column.

Base for mapping A-Z will be 26

Example¶

Warning

Please take some time to think about the solution approach on your own before reading further.....

Approach¶

Start with the given number n.
For each digit of the column title (from right to left):
Find the remainder when n is divided by 26.
Map the remainder to the corresponding letter ('A' to 'Y' for 1-25, 'Z' for 0).
Append the letter to the Excel column title.
Divide n by 26 (integer division) to process the next digit.
Repeat step 2 until n becomes zero.
The resulting string is the Excel column title for the original number n.

Code¶

void columnTitle(int n) {
    ans = "";
    while(n > 0) {
        ans = (char) ((n - 1) % 26 + 'A') + ans; // char + string
        n = (n - 1) / 26
    }
    return ans
}

Complexity¶

Time Complexity: O(log(N)) [base 26]
Space Complexity: O(1)