Maths 1: Modular Arithmetic & GCD¶

Modular Arithmetic Introduction¶

A % B = Remainder when A is divided by B

Range of A % B will be within [0, B - 1]

Why do we need Modular Arithmetic(%) ?¶

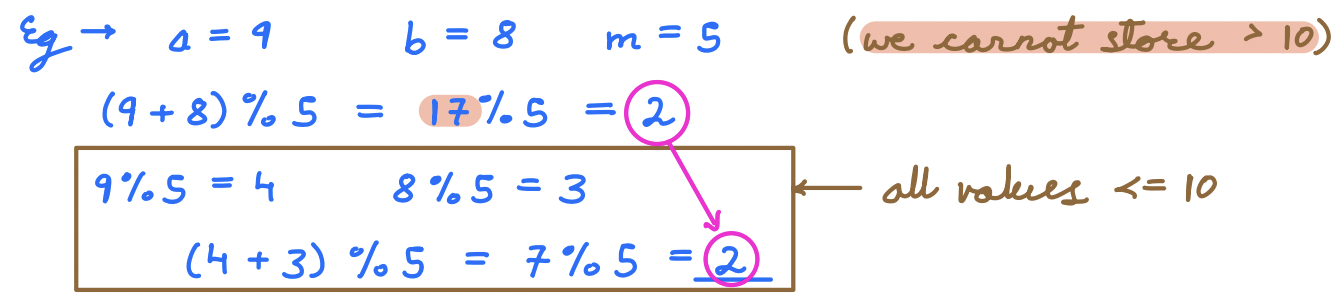
The most useful need of % is to limit the range of data. We don't have unlimited range in Integer OR Long, hence after a certain limit, we cannot store data. In such cases, we can apply mod to limit the range.

Rules for applying mod on Arithmetic Operations¶

1. (a + b) % m = (a % m + b % m) % m

Example:

2. (a * b) % m = (a % m * b % m) % m

3. (a + m) % m = (a % m + m % m) % m = (a % m) % m = a % m

4. (a - b) % m = (a % m - b % m + m) % m

This extra m term is added to ensure that the result remains within the range of 0 to m-1 even if the intermediate result of (a % m - b % m) is negative. This guarantees that the final remainder is a non-negative value.

Example:

Let's take a = 7, b = 10, and m = 5.

(a - b) % m = (7 - 10) % 5 = -3 % 5 = -3 (which is not in the range 0 to 4)

Now we can simly do (-3 + 5) % 5 = 2 (now value is in the range 0 to 4)

5. (a ^ b) % m = ( (a % m) ^ b ) % m (a raise to power b)

Question¶

Evaluate :

\((37^{103}-1)\%12\)

Choices

1
0
No Idea
10

Explanation:

\((37^{103}-1)\%12\)

\(=>~ ((37^{103}~\%12)-(1\%12)+12)\%12\)

\(=>~ (((37\%12){103}~\%12)-1+12)~\%12\)

\(=>~ (1-1+12)\%12 = 12\%12 =0\)

Question¶

What is the result of the following modular arithmetic operation? (25+13)%7

Choices

1
2
6
4

Explanation

(25+13)%7=38%7=3⋅7+3=3
Therefore, the correct choice is 6.

Question 1 Count pairs whose sum is a multiple of m¶

Given N array elements, find count of pairs (i, j) such that \((arr[i] + arr[j]) ~\%~ m = 0\)

Note: \(i~!=~j\) and pair(i, j) is same as pair(j, i)

Example

A[ ] = {4, 3, 6, 3, 8, 12}
m = 6

Pairs that satisfy \((arr[i] + arr[j]) ~\%~ 6 = 0\) are:

(4 + 8) % 6 = 0
(3 + 3) % 6 = 0
(6 + 12) % 6 = 0

Warning

Please take some time to think about the solution approach on your own before reading further.....

Brute Force Approach¶

For each pair of distinct indices i and j (where i != j), the sum \(arr[i] ~+~ arr[j]\) is calculated, and then the remainder of this sum when divided by m is checked.
If the remainder is 0, then the pair (i, j) satisfies the condition, and the count is incremented. This approach has a time complexity of \(O(N^2)\), where N is the number of elements in the array, as it involves checking all possible pairs.

Optimal Approach¶

Hint:

We can utilise the property: \((a + b) \% m = (a \% m + b \% m) \% m\) Instead of directly checking for \((a+b)\%m\), we can check for \((a ~\%~ m ~+~ b \% m) \% m\)

Idea:

Iterate through the array and calculate A[i] % m for all values.
Now, the sum of A[i] % m for two values should be divisible by m.

Example:

A[ ] = {2, 3, 4, 8, 6, 15, 5, 12, 17, 7, 18}
m = 6

After doing mod with 6, we'll get

{2, 3, 4, 2, 0, 3, 5, 0, 5, 1, 0}
Note: The range of A[i] % 6 is from 0 to 5

Summing 1 with 5 will give sum divisible by 6.
Likewise, 2 with 4, 3 with 3, and lastly 0 with 0.

Algorithm¶

Iterate given array and calculate \(A[i]\%m\).
Create a frequency array of size m to store the frequency of remainders obtained from the elements.
For each element, find the complement remainder needed for the sum to be divisible by m. Count frequency of complement remainder. Add these counts to get the total count of pairs satisfying the condition.
Note: Mod 0 will form a pair with 0, i.e if m = 6, and say 12 & 18 are present in given array, doing 12 % 6 and 18 % 6 will result in 0.

Dry Run¶

A[ ] = {2, 3, 4, 8, 6, 15, 5, 12, 17, 7, 18}
m = 6

After doing mod with 6, we'll get

{2, 3, 4, 2, 0, 3, 5, 0, 5, 1, 0}

We'll keep inserting frequency of elements in frequency array while iterating over remainder values -

Remainder	Pair for it	Frequency	Count	Freq array
2	\(6-2 = 4\)	4 is not yet present, but insert 2 for future use.	0	2:1
3	\(6-3 = 3\)	3 is not yet present, but insert 3 for future use.	0	2:1 3:1
4	\(6-4 = 2\)	2 is present with freq 1, count += 1 i.e, 1; insert 4 for future use	1	2:1 3:1 4:1
2	\(6-2 = 4\)	4 is present with freq 1, count += 1 i.e, 2; update frequency of 2.	2	2:2 3:1 4:1
0	0 forms pair with 0	0 is not yet present, but insert 0 for future use.	2	2:2 3:1 4:1 0:1
3	\(6-3 = 3\)	3 is present with freq 1, count += 1 i.e, 3; update frequency of 3.	3	2:2 3:2 4:1 0:1
5	\(6-5 = 1\)	1 is not yet present, but insert 5 for future use.	3	2:2 3:2 4:1 0:1 5:1
0	0 forms pair with 0	0 is present with freq 1, count += 1 i.e, 4; update frequency of 0.	4	2:2 3:2 4:1 0:2 5:1
5	\(6-5 = 1\)	1 is not yet present, but update frequency of 5	4	2:2 3:2 4:1 0:2 5:2
1	\(6-1 = 5\)	5 is present with freq 2, count += 2 i.e, 6; update frequency of 1.	6	2:2 3:2 4:1 0:2 5:2 1:1
0	0 forms pair with 0	0 is present with freq 2, count += 2 i.e, 8; update frequency of 0.	8	2:2 3:2 4:1 0:3 5:2 1:1

Pseudocode¶

int pairSumDivisibleByM(A, m) {
    N = A.length;
    freq[N] = {
        0
    };
    count = 0;

    for (int i = 0; i < N; i++) {
        val = A[i] % m;

        if (val == 0) {
            pair = 0;
        } else {
            pair = m - val;
        }
        ans += freq[pair];
        freq[val]++;
    }

    return count;
}

Time Complexity - O(N)

Question¶

Space Complexity: Pair Sum Divisible by M

Choices

O(N)
O(M)
O(N+M)

Explanation

Space Complexity (SC) is O(M), where M is the modulus value. This is because the frequency array of size M is required to store frequency of elements from 0 to M-1.

GCD Basics¶

Explanation¶

GCD - Greatest Common Division
HCF - Highest Common Factor
GCD(A, B) - Greatest factor that divides both a and b

If we have GCD(A, B) = x

This implies:-

A % x = 0
B % x = 0

and hence x is the highest factor of both A and B

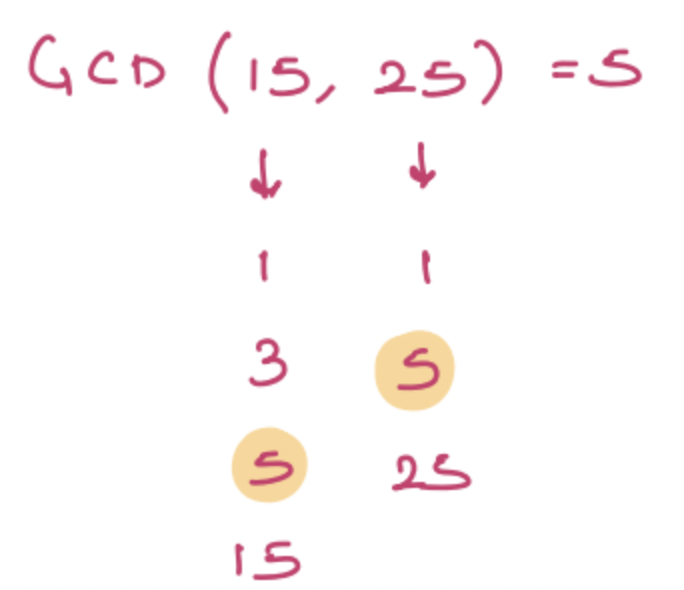
Example - 1

GCD(15, 25) = 5

Example - 2

GCD(12, 30) = 6

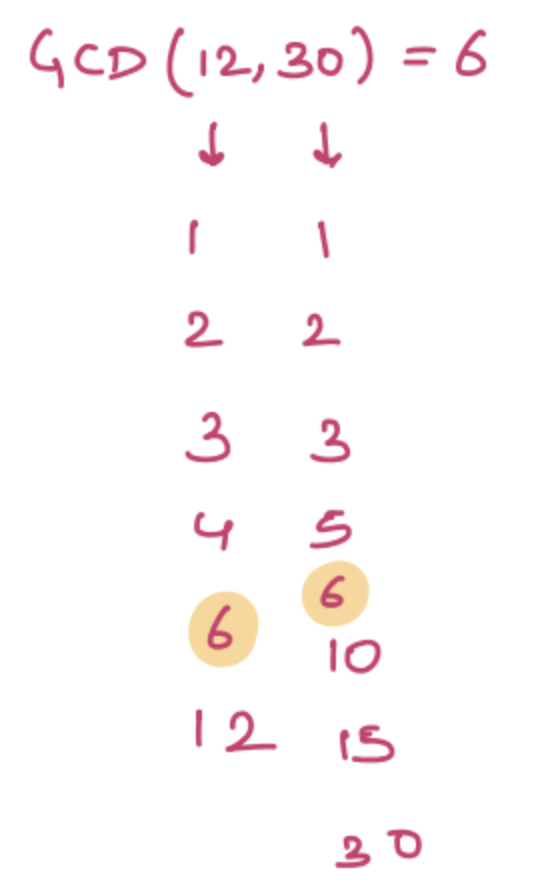
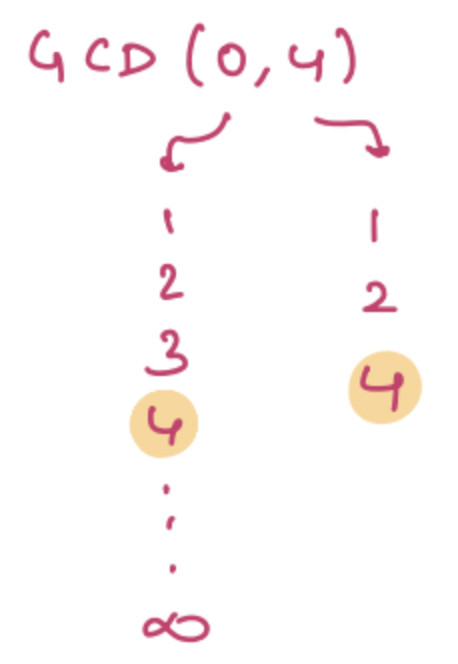
Example - 3

GCD(0, 4) = 4

Example - 4

GCD(0, 0) = Infinity

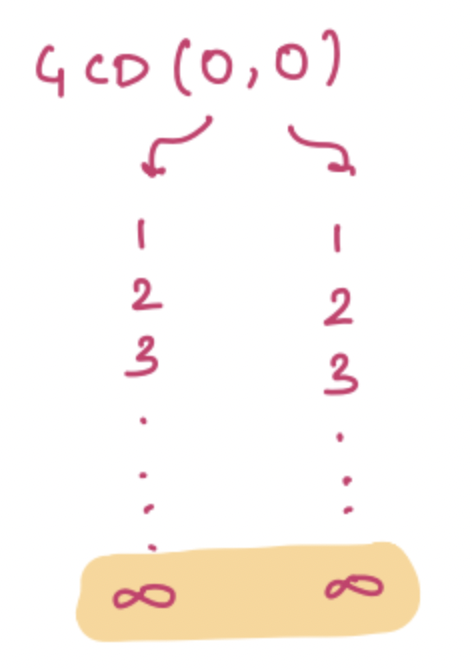
Properties of GCD¶

Property - 1¶

GCD(A, B) = GCD(B, A)

Property - 2¶

GCD(0, A) = A

Property - 3¶

GCD(A, B, C) = GCD(A, GCD(B, C)) = GCD(B, GCD(C, A)) = GCD(C, GCD(A, B))

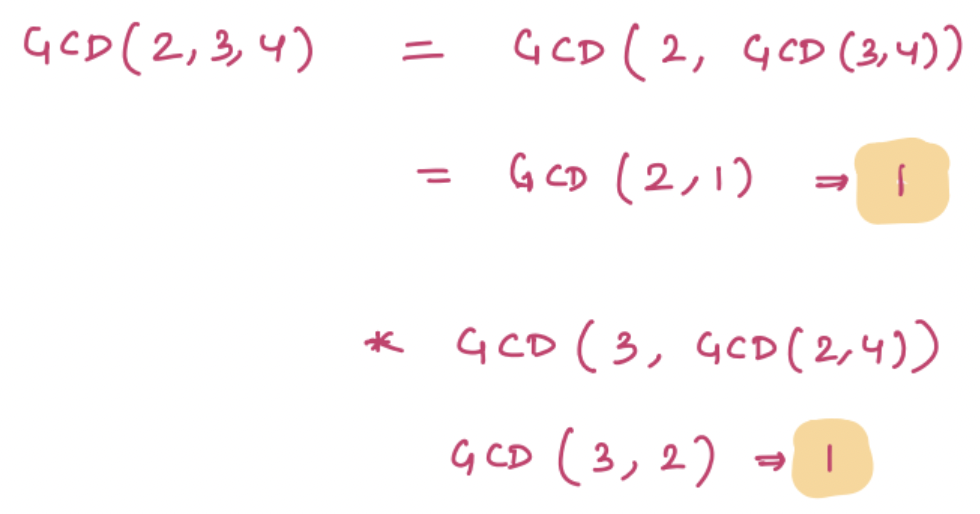
Property - 4¶

Given A >= B > 0, GCD(A, B) = GCD(A - B, B)

Example:

Property - 5¶

GCD(A, B) = GCD(A % B, B)

Question¶

gcd(0,8) = ?
Chose the correct answer

Choices

1
8
0
not defined

Question¶

TC of gcd(a1,a2,a3,....,an) is:
Chose the correct answer

Choices

O(log(max number))
O(N)
O(N*log(max number)
O(N^2)

Question¶

Given an array A = [15, 21, 33, 45], find the GCD of all elements in the array.

Choices

4
3
6
9

Function of GCD¶

Write a function to find GCD(A, B)¶

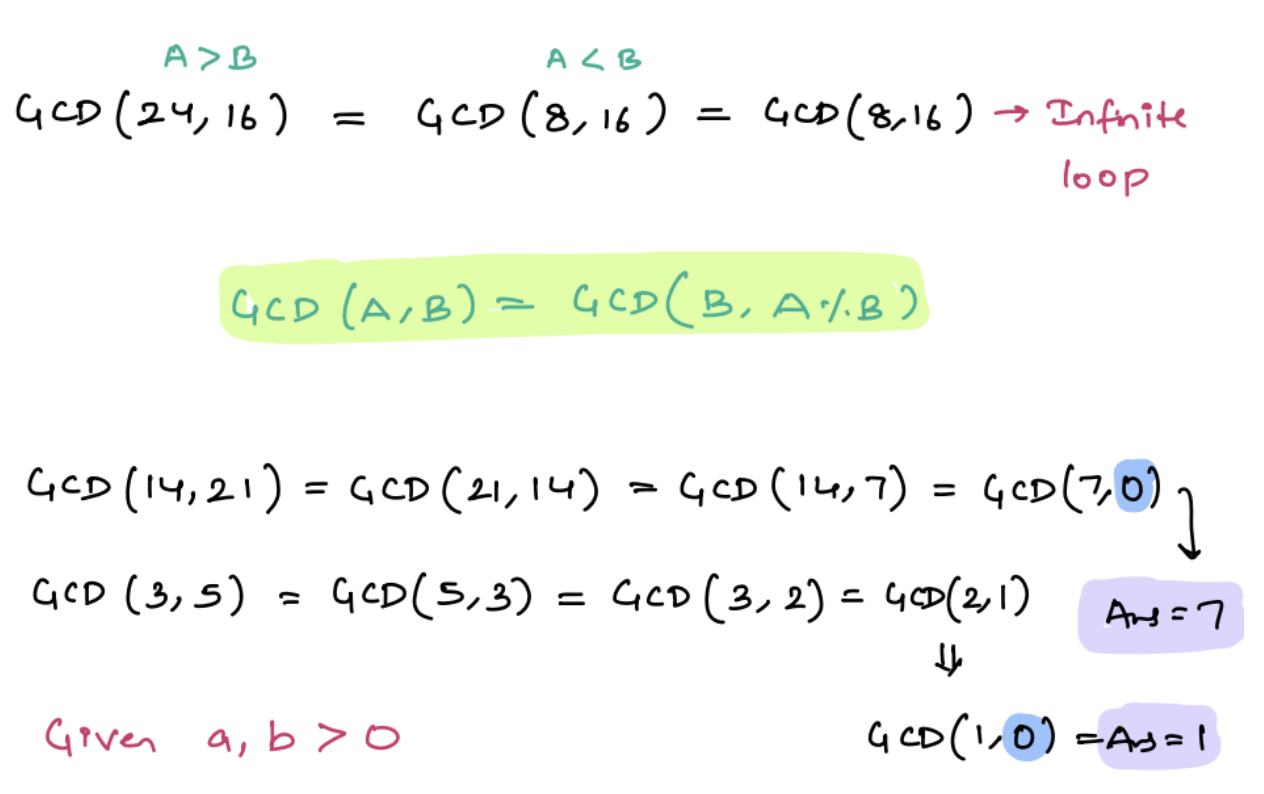
Suppose we have two positive numbers a, b then:

int gcd(a, b) {
    if (b == 0) {
        return a;
    }
    return gcd(b, a % b);
}

Time Complexity(TC): O(log(max(a, b)))

Given an array, calculate GCD of the entire array¶

Example:

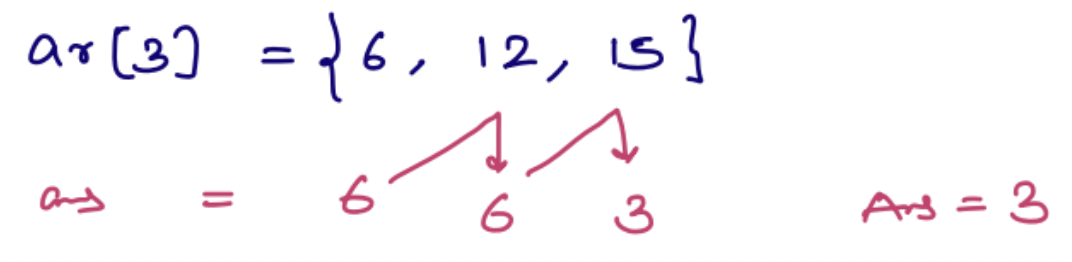
int gcdArr(int[] arr) {
    int ans = arr[0];
    int n = arr.length();
    for (int i = 0; i < n; i++) {
        ans = gcd(ans, arr[i])
    }
    return ans;
}

Problem 2 Delete One¶

Question

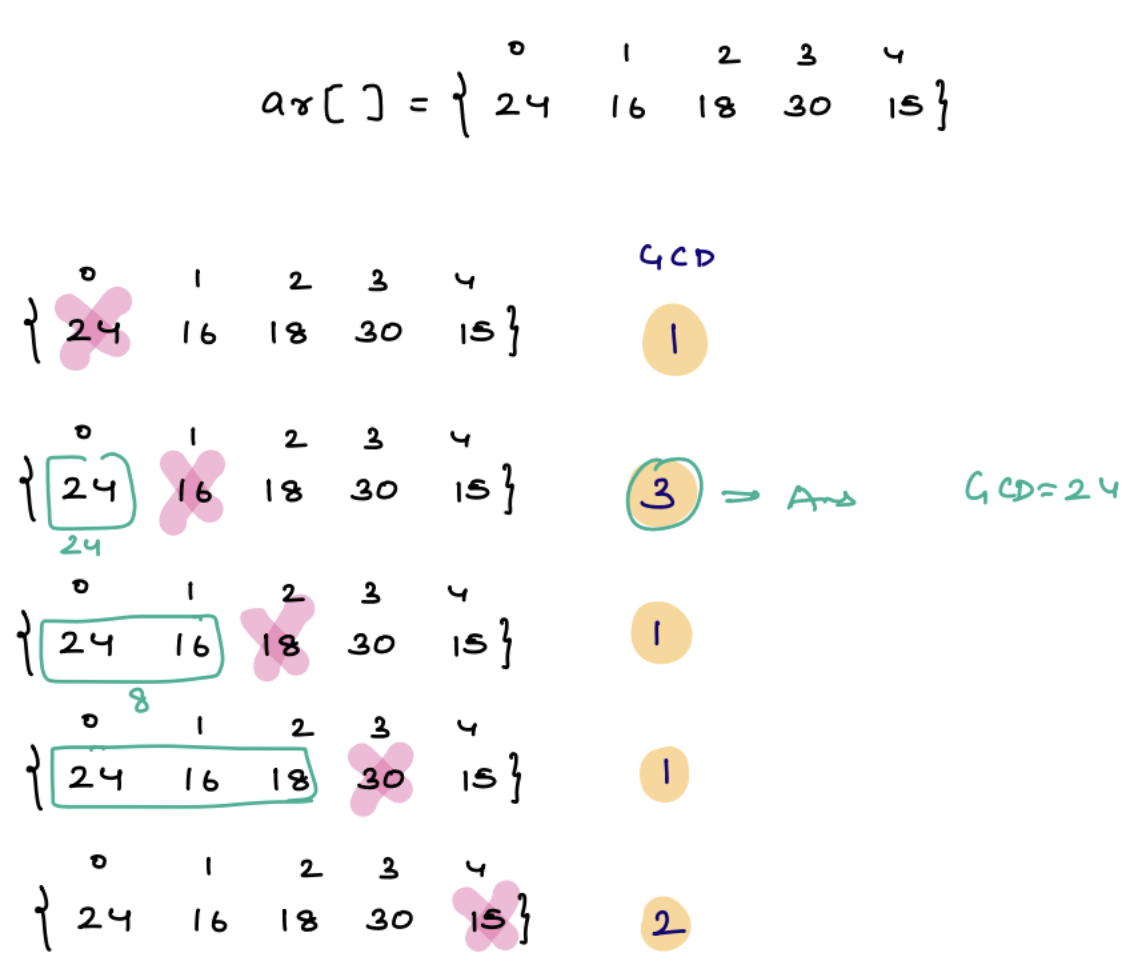
Given arr[N] elements , we have to delete one element such that GCD of the remaining elements becomes maximum.

Example:

Brute Force Approach¶

The brute approach for this problem will be to delete arr[i], and then calculate the GCD for all the remaining elements. This will be repeated for all the elements.

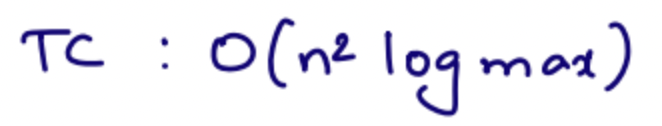
Warning

Please take some time to think about the optimised approach on your own before reading further.....

Optimal Approach: Prefix Array¶

Approach:

Idea is to find the GCD value of all the sub-sequences of length (N – 1) and removing the element which is not present in the sub-sequence with that GCD. The maximum GCD found would be the answer.
To find the GCD of the sub-sequences optimally, maintain a prefixGCD[] and a suffixGCD[] array using single state dynamic programming.
The maximum value of GCD(prefixGCD[i – 1], suffixGCD[i + 1]) is the required answer.

The implementation is given below:

 // Recursive function to return gcd of a and b
    static int gcd(int a, int b) {
        if (b == 0)
            return a;
        return gcd(b, a % b);
    }

    static int MaxGCD(int a[], int n) {

        // Prefix and Suffix arrays
        int Prefix[] = new int[n + 2];
        int Suffix[] = new int[n + 2] ;

        Prefix[1] = a[0];
        for (int i = 2; i <= n; i += 1) {
            Prefix[i] = gcd(Prefix[i - 1], a[i - 1]);
        }

        Suffix[n] = a[n - 1];
        for (int i = n - 1; i >= 1; i -= 1) {
            Suffix[i] = gcd(Suffix[i + 1], a[i - 1]);
        }

        // If first or last element of the array has to be removed
        int ans = Math.max(Suffix[2], Prefix[n - 1]);

        // If any other element is replaced
        for (int i = 2; i < n; i += 1) {
            ans = Math.max(ans, gcd(Prefix[i - 1], Suffix[i + 1]));
        }
        return ans;
    }

Maths 1: Modular Arithmetic & GCD¶

Modular Arithmetic Introduction¶

Why do we need Modular Arithmetic(%) ?¶

Rules for applying mod on Arithmetic Operations¶

Question¶

Question¶

Question 1 Count pairs whose sum is a multiple of m¶

Brute Force Approach¶

Optimal Approach¶

Algorithm¶

Dry Run¶

Pseudocode¶

Question¶

GCD Basics¶

Explanation¶

Properties of GCD¶

Property - 1¶

Property - 2¶

Property - 3¶

Property - 4¶

Property - 5¶

Question¶

Question¶

Question¶

Function of GCD¶

Write a function to find GCD(A, B)¶

Given an array, calculate GCD of the entire array¶

Problem 2 Delete One¶

Brute Force Approach¶

Optimal Approach: Prefix Array¶

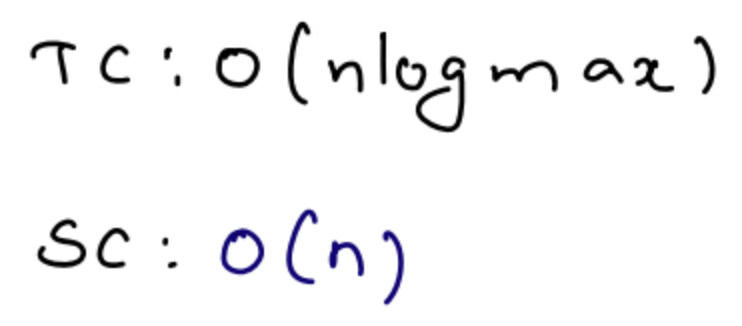
Proof of gcd(a, b) = gcd(a-b, b)¶