Maths 3: Prime Numbers¶

Introduction to Prime Numbers¶

What are Prime Numbers?¶

Numbers having only 2 factors i.e, 1 and the number itself are known as Prime Numbers

Example:

2, 5, 7, 11

Problem 1 Check if a number is prime or not¶

Given a number, we need to check wheather its a prime number or not

Example

Input:

n = 3

n = 4

Output:

true

false

Question¶

Check whether 11 is a prime number or not!

Choices

true, 11 is a prime number
false, 11 is not a prime number

Approach¶

We need to count the number of factors:
- if factors = 2, then it is prime
- otherwise if factors >2, then it is non prime

Code snippet¶

boolean checkPrime(int n) {
    count = 0;
    for (int i = 1; i * i <= n; i++) {
        if (n % i == 0) {
            if (i == n / i) {
                count++;
            } else {
                count += 2;
            }
        }
    }
    if (count == 2) {
        print("prime");
    } else {
        print("Not Prime");
    }
}

Problem 2 Print all prime numbers from 1 to N¶

Given a number N, we need to print all the prime no. from 1 to N

Example

Question¶

Find all the prime numbers from 1 to N

Choices

1, 2, 3, 5, 7
2, 3, 5, 7, 8
2, 3, 5, 7
2, 5 ,7

Solution¶

Brute Force: Iterate from 1 to N, and check if a number is prime or not.

void printAllPrime(int n) {
        for (int i = 2; i <= n; ++i) {
            boolean isPrime = true;
            for (int j = 2; j * j <= i; ++j) {
                if (i % j == 0) {
                    isPrime = false;
                    break;
                }
            }
        }

Time Complexity (TC): The time complexity of the given function is \(O(n√n)\), as it iterates through numbers from 2 to N and for each number, it checks divisibility up to the square root of that number.
Space Complexity (SC): The space complexity is O(1), as the function uses a constant amount of extra space regardless of the input size.

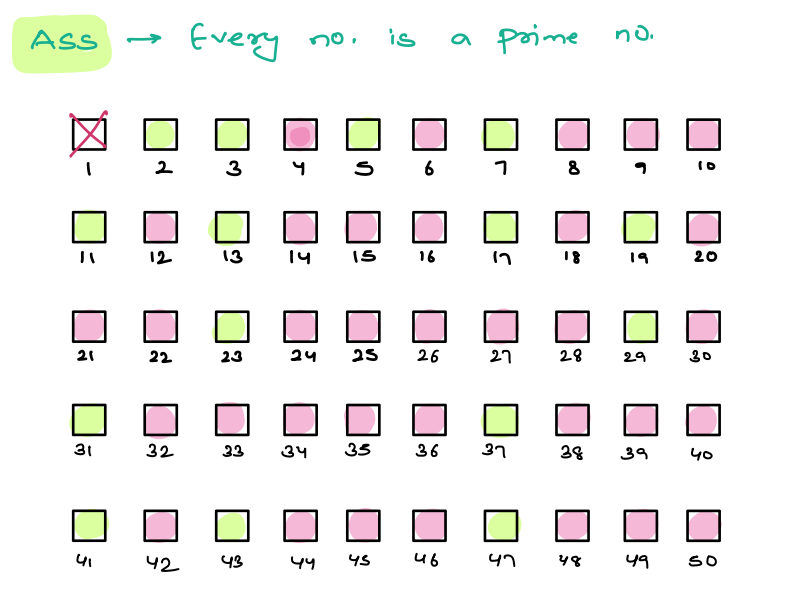
Sieve of Eratosthenes¶

Optimized approach for counting number of primes between 1 to N¶

Approach

Assumption: Begin by assuming that all numbers from 2 to N are prime numbers.
Marking Non-Primes: Start with the first prime number, which is 2. Since 2 is a prime number, mark all its multiples as non-prime. These multiples are 4, 6, 8, and so on.
Move to Next Unmarked Number: Move to the next unmarked number, which is 3. Since 3 is a prime number, mark all its multiples as non-prime. These multiples are 6, 9, 12, and so on. Notice that we skip numbers that have already been marked as non-prime in previous steps. Unmarked numbers are prime as they do not have any number less then themselves a factor of the number except 1. Which means they are prime
Repeat for Remaining Unmarked Numbers: Continue this process for the remaining unmarked numbers, each time marking all their multiples as non-prime.
Completion: After going through all numbers up to the square root of N, the remaining unmarked numbers are prime numbers. This is because their multiples have been marked as non-prime in previous steps.

Code Snippet¶

void printAllPrime(int n) {
    boolean[] isPrime = new boolean[n + 1]; // Initialize a boolean array to track prime numbers
    Arrays.fill(isPrime, 2, n + 1, true); // Assume all numbers from 2 to n are prime

    for (int i = 2; i * i <= n; ++i) {
        if (isPrime[i]) {
            for (int j = i * i; j <= n; j += i) {
                isPrime[j] = false; // Mark multiples of the current prime as non-prime
            }
        }
    }
}

Optimization in Sieve of Eratosthenes¶

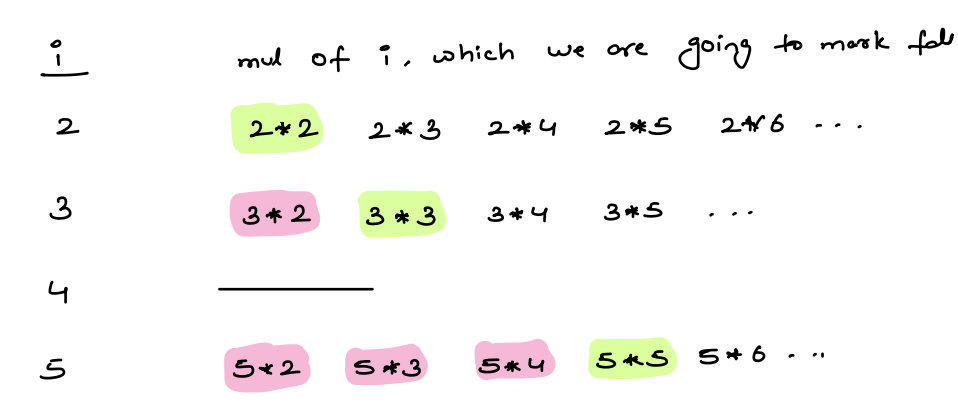
Starting from the square of each prime number, mark all its multiples as non-prime in the sieve. This is efficient because smaller multiples of the prime would have already been marked by smaller primes. By avoiding redundant marking, we optimize the Sieve of Eratosthenes algorithm.

Time Complexity (TC): The optimized Sieve of Eratosthenes has a time complexity of O(n log log n), which means it grows very slowly. This is because the algorithm only visits and marks numbers up to the square root of N, and the number of non-prime numbers marked is logarithmic with respect to N.
Space Complexity (SC): The space complexity is O(n), which is used to store the boolean array indicating whether each number is prime or not. The space used is directly proportional to the input size N.

Problem 3 Smallest Prime Factor¶

Given N, return the smallest prime factors for all numbers from 2 to N

Example:

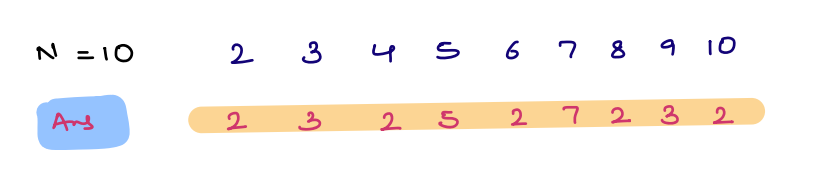
Question¶

What is the smallest prime factor of 25

Choices

1
5
10
25

Warning

Please take some time to think about the solution approach on your own before reading further.....

Smallest Prime Factor Approach¶

Initialization: Create an integer array to store the smallest prime factors for each number from 2 to N. Initialize each element of the array to its own value, indicating that it's not yet known if the number is prime or not.
Smallest Prime Factor Determination: Starting from the first prime number (2), for each prime number:
- If the smallest prime factor for a number is still its own value (indicating it's not determined yet), mark it as the smallest prime factor for all its multiples.
Iterate Over All Numbers: Go through each number from 2 to N, and for each number, if its smallest prime factor is still itself, mark it as prime and set its smallest prime factor to itself.
Smallest Prime Factors: The array will now hold the smallest prime factors for all numbers from 2 to N.

public int[] smallestPrimeFactors(int n) {
    int[] spf = new int[n + 1];

    for (int i = 2; i <= n; ++i) {
        spf[i] = i; // Initialize smallest prime factor with its own value

        if (spf[i] == i) { // i is prime
            for (int j = i * i; j <= n; j += i) {
                if (spf[j] == j) {
                    spf[j] = i; // Mark smallest prime factor for multiples
                }
            }
        }
    }

    return spf;
}

Prime Factorization¶

Prime factorization is the process of finding the prime numbers, which are multiplied together to get the original number. For example, the prime factors of 16 are \(2 × 2 × 2 × 2\).

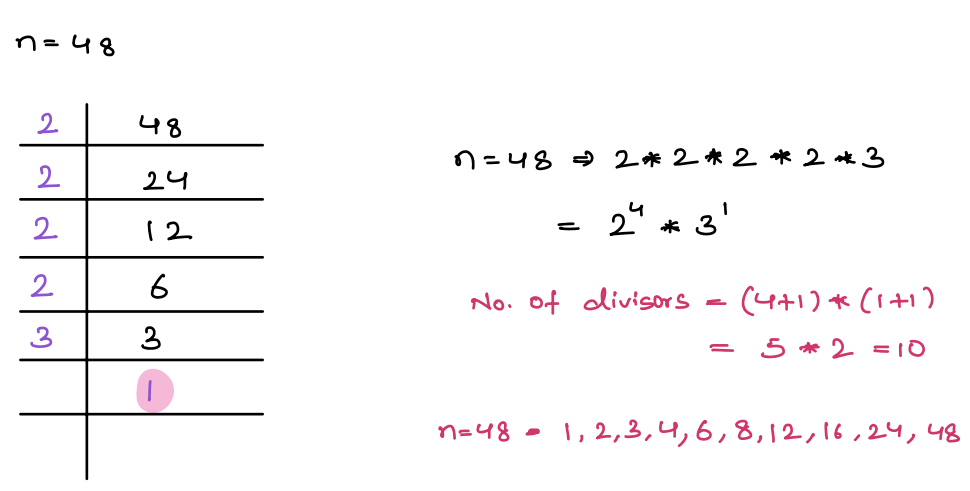
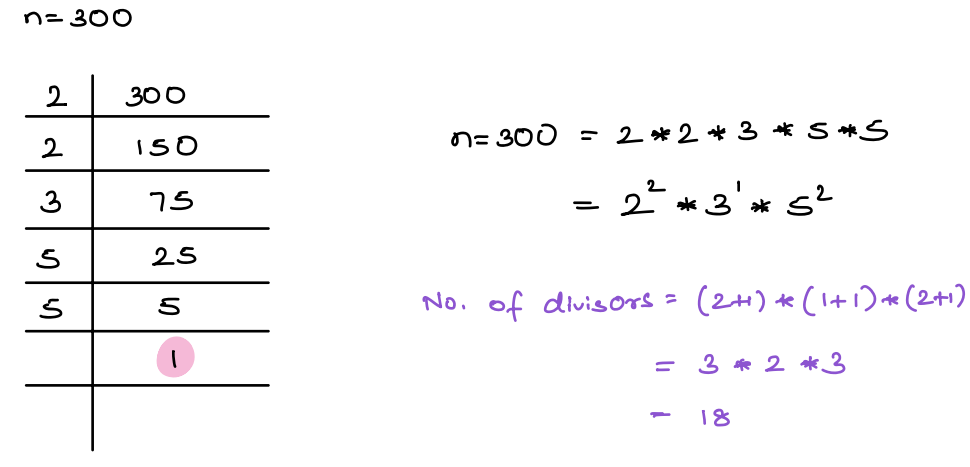
Problem 4 Total Number of Factors¶

Given a number n, assume its prime factorization

\(n=i^{a1}*j^{a2}*k^{a3}...z^{ax}\)

the number of choices we have for the power of every prime is [0, a1], [0,a2], [0, a3].............[0, ax]

the number of divisor/factors will be given by the formula:

(a1 + 1)(a2 + 1)(a3 + 1)*.....(ax + 1)

Example 1

\(25 = 5^2\)

Number of divisors = \((2+1) = 3\)

Example 2

Question¶

Find the total number of factors of 20

Choices

5
1
3
4

Explanation:

20 = 2² * 5¹
= (2 + 1) * (1 + 1)
= 5

The factors are 1, 2, 5, 10, 20.

Warning

Please take some time to think about the solution approach on your own before reading further.....

Total Number of Factors Approach¶

Approach¶

Prime Factorization: For each number from 1 to N, find its prime factorization. Determine the prime factors of the number and their respective powers.
Counting Factors: The number of factors for a given number is calculated by adding 1 to each power of its prime factors and then multiplying those incremented powers together.
Iterate through Numbers: Iterate through the numbers from 1 to N. For each number:
- Calculate its prime factorization.
- Count the factors using the prime factors' powers.
Store or Output Results: Store or output the number of factors/divisors for each number.

The number of factors for a given number is calculated by adding 1 to each power of its prime factors and then multiplying those incremented powers together.

For 1: \((1+1) = 2\) factors (1 and itself).
For 2: \((1+1) = 2\) factors (1 and 2).
For 3: \((1+1) = 2\) factors (1 and 3).
For 4: \((2+1) = 3\) factors (1, 2, and 4).
For 5: \((1+1) = 2\) factors (1 and 5).
For 6: \((1+1) * (1+1) = 4\) factors (1, 2, 3, and 6).
For 7: \((1+1) = 2\) factors (1 and 7).
For 8: \((3+1) = 4\) factors (1, 2, 4, and 8).
For 9: \((2+1) = 3\) factors (1, 3, and 9).
For 10: \((1+1) * (1+1) = 4\) factors (1, 2, 5, and 10).

Code¶

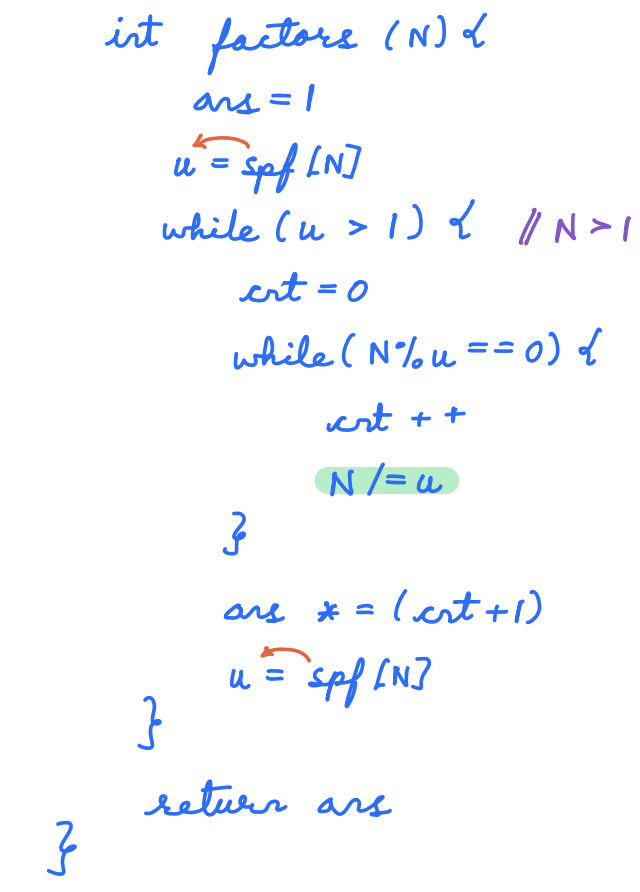
Time Complexity (TC): The time complexity of this code is O(N * log N), mainly due to the prime factorization process for each number from 1 to N.
Space Complexity (SC): The space complexity is O(N), where the primary space usage comes from the arrays for storing the smallest prime factors and the hashmap for storing the factors count for each number.