Graphs 3: MST & Dijkstra

---

Challenges in Flipkart's Logistics and Delivery

Scenario:

Suppose Flipkart has N local distribution centers spread across a large metropolitan city. These centers need to be interconnected for efficient movement of goods. However, building and maintaining roads between these centers is costly. Flipkart's goal is to minimize these costs while ensuring every center is connected and operational.

Goal:

You are given number of centers and possible connections that can be made with their cost. Find minimum cost of constructing roads between centers such that it is possible to travel from one center to any other via roads.

Explanation

Example:

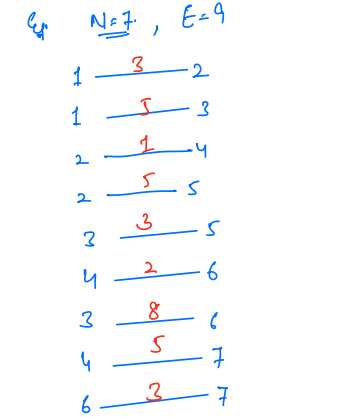
Output:

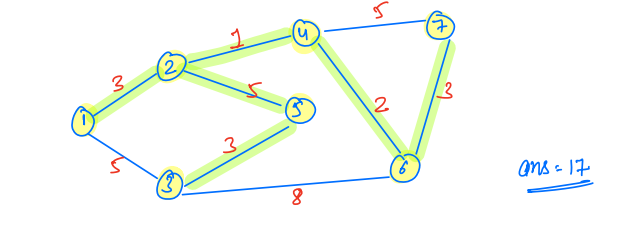
Idea:

To achieve the lowest cost in our scenario, consider these key points:

1. Aim for Fewer roads:

Minimizing the number of roads directly leads to reduced costs.

1. Opt for a Tree Structure:

Why a tree? Well, in the world of data structures, a tree uniquely stands out when it comes to minimal connections. For any given N nodes, a tree is the only structure that connects all nodes with exactly N - 1 edges. This is precisely what we need - the bare minimum of edges to connect all points, ensuring the lowest possible number of roads.

Another Example:

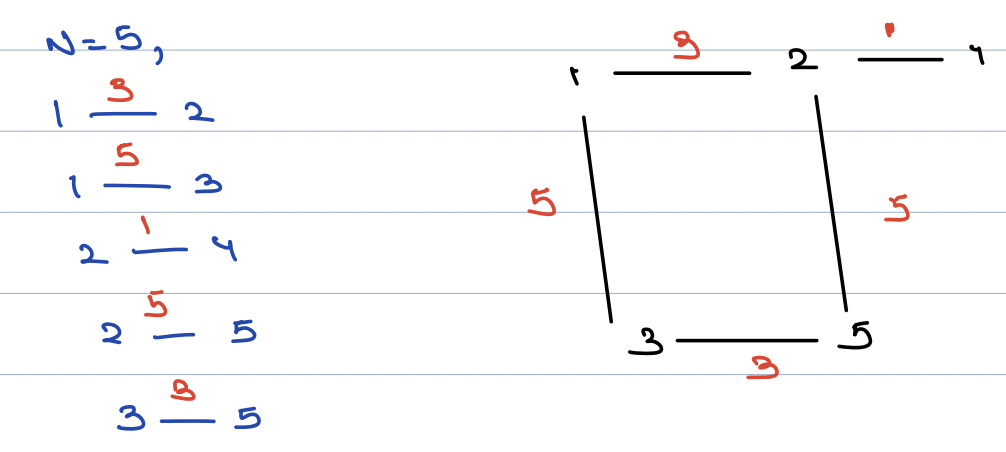
The end goal is that all centers should be connected.

Possible Solutions -

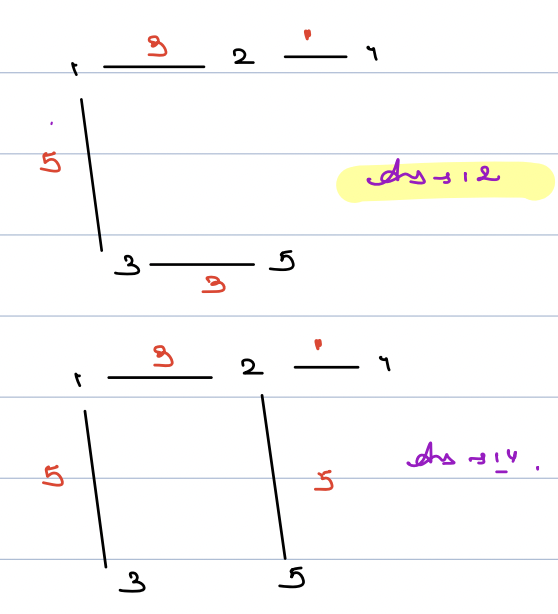
Here first is better because the sum of all edge weights is minimum.

The tree which spans (covers) all the vertices with the minimum number of edges needed to connect them is known as Spanning Tree.

Minimum Spanning Tree

The minimum spanning tree has all the properties of a spanning tree with an added constraint of having the minimum possible weights among all possible spanning trees.

Uniqueness of MST:

If all edge weights are unique, there's only one MST. If some weights are the same, multiple MSTs can exist.

Algorithms for MST:

Kruskal's and Prim's algorithms are used to find MSTs. The MST found can vary based on the choices made for edges with equal weights. Both algorithms solve for same problem having same time and space complexities.

Solution to Flipkart's problem

Application of MST:

• Identify All Possible Connections:

First, identify all the possible routes that can connect these N centers. Imagine this as a network where each center is a node, and each possible road between two centers is an edge.

• Assign Costs:

Assign a cost to each potential road, based on factors like distance, traffic, or construction expenses. In real-life terms, shorter and more straightforward routes would generally cost less.

• Create the MST:

Now, apply the MST algorithm (like Kruskal's or Prim's). The algorithm will select routes that connect all the centers with the least total cost, without forming any loops or cycles.

• Outcome:

The result is a network of roads connecting all centers with the shortest total length or the lowest cost.

---

Prim's Algorithm

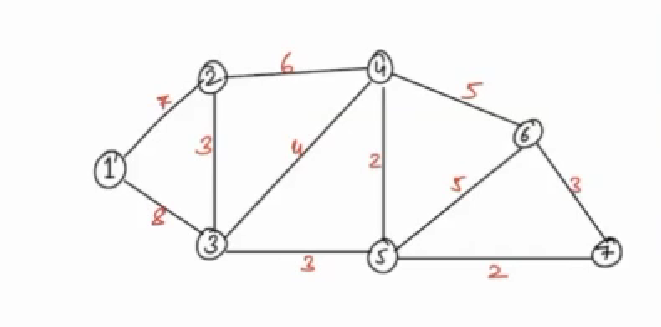
Let's consider the below Graph:

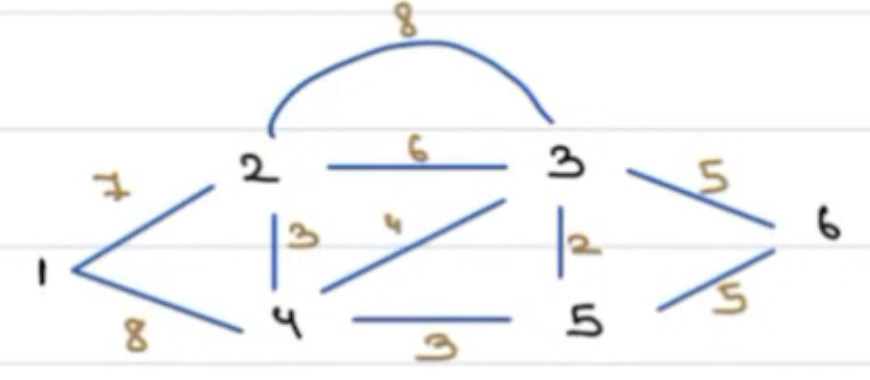
Say we start with vertex 5, now we can choose an edge originating out of 5.

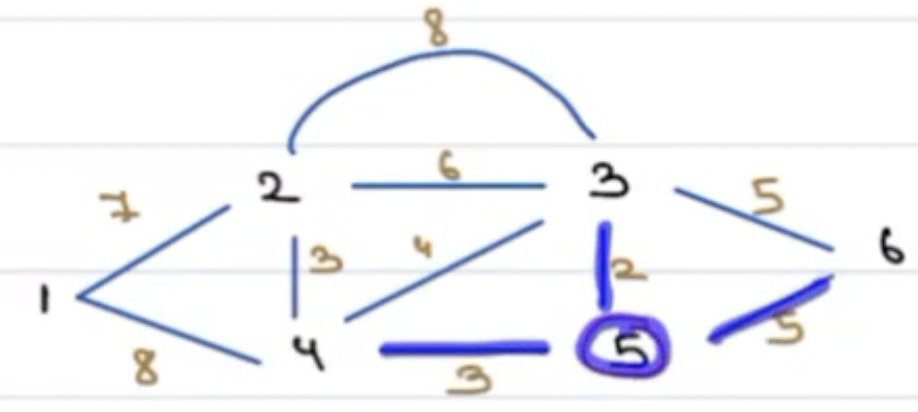
Which one should we choose?

The one with minimum weight.

We choose 5 ---- 3 with weight 2

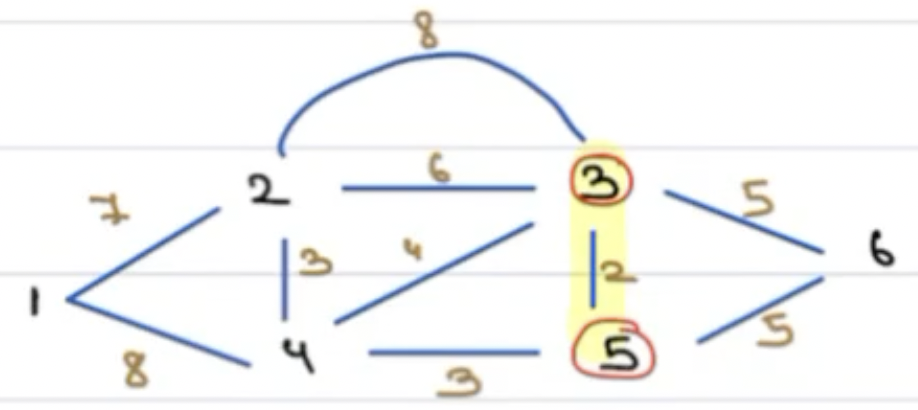
Now, after this, since 5 and 3 are part of the MST, we shall choose a min weighted edge originated from either 3 or 5. That edge should connect to a vertex which hasn't been visited yet.

We choose 5 ---- 4 with weight 3

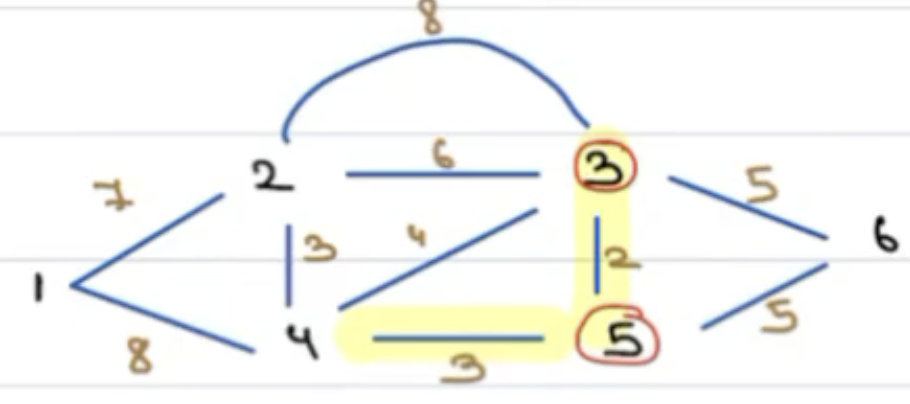
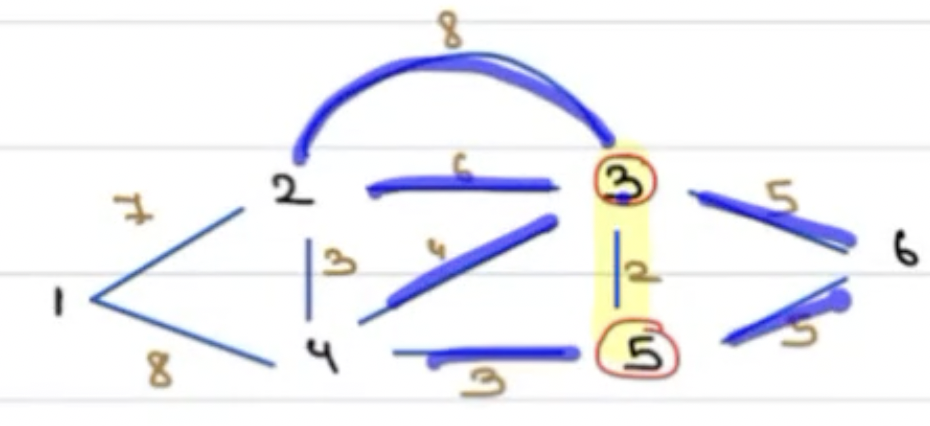
Now, same process follows i.e, we can select a min weighted edge originating from 3, 4, or 5 such that it should connect to a vertex that hasn't been visited yet.

After completing the entire process, we shall have below MST.

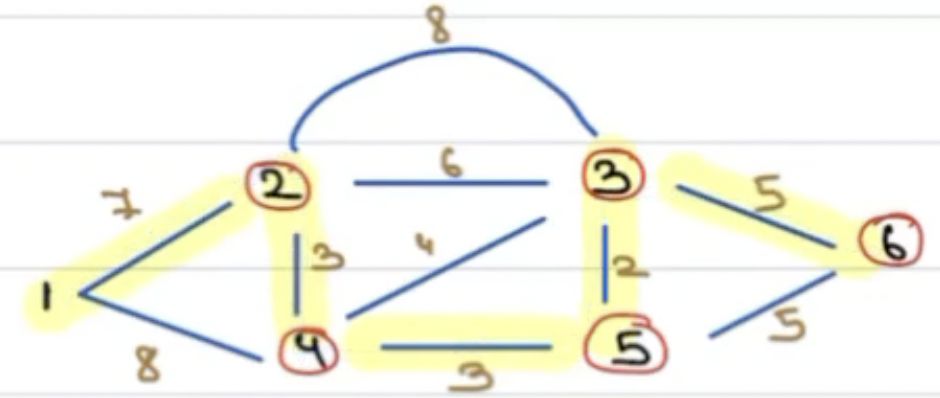
Execution

Say we have a black box(we'll name it later)

Now, say we start with 5. From 5, via weight 3 we can visit 4, via weight 5 we can visit 6, via weight 2 we can visit 3.

We'll information as - (weight, vertex)

From this, we'll get vertex reachable via min weight, which data structure can be helpful ?

MIN HEAPS

Now, we remove (2, 3) from heaps and connect 3 to 5.

From 3, the nodes that are reachable will be pushed to the heap.
We'll insert only those vertices which haven't been visited yet.

Select the minimum weighted -> (3, 4)

Now, this shall continue.

Pseudocode

while (!heap.isEmpty()) {

    Pair p = heap.getMin();

    if (vis[v] == true)
        continue;

    // Add the vertex to the MST and accumulate the weight
    vis[v] = true;
    ans += p.first

    // Now, you can optionally iterate through the adjacent vertices of 'v' and update the heap with new edges
    for ((u, w) in adj[v]) {

        if (!vis[u]) {
            // Add the unvisited neighbor edges to the heap
            heap.add({w,u});
        }
    }
}

Complexity

Time Complexity: O(E * logE)
Space Complexity: O(V + E)

---

Dijkstra’s Algorithm

There are N cities in a country, you are living in city-1. Find minimum distance to reach every other city from city-1.

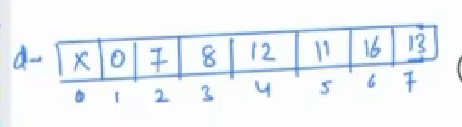
We need to return the answer in the form of array

Output:

Initialize Data Structures:

• Create an adjacency list (graph) to represent the cities and their distances.
• Initialize a distances list with infinity for all cities except city-1 (set to 0).
• Use a Heap<pair> (heap) to explore cities, starting with the pair (0, 0) (distance from city-1 is 0, and it's city-1 itself). The heap will contain <Distance from the source vertex of a node, node>.

Explore Cities:

• While heap is not empty:
  • Pop the pair (dist, u) with the shortest known distance.
  • If dist is greater than the known distance to the city u, skip it.
  • Otherwise, update the distance and explore its neighbors.

Explore Neighbors:

• For each neighbor of city u in the graph:
  • Calculate the distance from city-1 via city u.
  • If this new distance is shorter, update it and add the pair (new_distance, v) to the heap, where v is the neighbor.

Termination:

• Continue until the heap is empty, exploring all cities.

Return Result:

• The distances list now holds the minimum distances from city-1 to all other cities.

  while (!hp.isEmpty()) {
     Pair rp = hp.poll(); // Extract the minimum element

     int d = rp.first; // Distance
     int u = rp.second; // City

     // Skip if this distance is greater than the known distance
     if (d > dist[u]) {
         continue;
     }

     // Explore neighbors of u and update distances
     for ( /* Loop through neighbors */ ) {
         int v = /* Neighbor city */ ;
         int w = /* Weight to reach v from u */ ;

         // Calculate the new distance via u
         int new_dist = dist[u] + w;

         // If the new distance is shorter, update dist and add to heap
         if (new_dist < dist[v]) {
             dist[v] = new_dist;
             hp.add(new Pair(new_dist, v));
         }
     }
}

• The time complexity of the Dijkstra's algorithm implementation with a min-heap of pairs is \(O((E + V) * log(V))\), where E is the number of edges, V is the number of vertices (cities), and log(V) represents the complexity of heap operations.
• The space complexity of this implementation is O(V + E), where V is the space used to store the dist array (minimum distances) for all cities, and E is the space used to represent the graph (adjacency list).

Can Dijkstra's algorithm work on negative wieghts?

Dijkstra's algorithm is not suitable for graphs with negative edge weights as it assumes non-negative weights to guarantee correct results. Negative weights can lead to unexpected behavior and incorrect shortest path calculations.

---