Arrays 1: One Dimensional¶

Problem 1 Find Maximum Subarray Sum¶

Problem Statement¶

Given an integer array A, find the maximum subarray sum out of all the subarrays.

Examples¶

Example 1: For the given array A with length N,

Index	0	1	2	3	4	5	6
Array	-2	3	4	-1	5	-10	7

Output:

Max Sum: 11
Subarray: 3 4 -1 5

Example 2: For the given array A with it's length as N we have,

Index	0	1	2	3	4	5	6
Array	-3	4	6	8	-10	2	7

Output:

Max Sum: 18
Subarray: 4 6 8

Question¶

For the given array A, what is the maximum subarray sum ?

A[ ] = { 4, 5, 2, 1, 6 }

Choices

6
18
No Idea
10

Max Sum: 18
Subarray: 4 5 2 1 6

Question¶

For the given array A, what is the maximum subarray sum ?

A[ ] = { -4, -3, -6, -9, -2 }

Choices

-9
18
-2
-24

Max Sum: -2
Subarray: -2

Find Maximum Subarray Sum Brute Force¶

Brute Force¶

No of possible subarrays: N * (N + 1) / 2

Iterate over all subarrays, calculate sum and maintain the maximum sum.

Psuedocode:¶

ans = A[0];
for (i = 0; i < N; i++) { // start to N
    for (j = i; j < N; j++) { // end
        for (k = i; k <= j; k++) {
            sum += A[k];
        }
        ans = Math.max(ans, sum);
        sum = 0; // Reset sum for the next iteration
    }
}
return ans;

Complexity¶

Time Complexity: O(N^2 * N) = O(N^3)
Space Complexity: O(1)

Warning

Please take some time to think about the optimised approach on your own before reading further.....

Find Maximum Subarray Sum using Carry Forward¶

Optimized Solution using Carry Forward¶

We don't really need the third loop present in brute force, we can optimise it further using Carry Forward technique.

Psuedocode¶

ans = A[0]
for (i = 0 to N - 1) { //start to N
    sum = 0
    for (j = i to N - 1) { //end
        sum += A[k]
        ans = max(ans, sum)
    }
}
return ans;

Complexity¶

Time Complexity: O(N^2)
Space Complexity: O(1)

Find Maximum Subarray Sum using Kadanes Algorithm¶

Observation:¶

Case 1:

If all the elements in the array are positive

Arr[] = [4, 2, 1, 6, 7]

Answer:

To find the maximum subarray we will now add all the positive elements

Ans: (4 + 2 + 1 + 6 + 7) = 20

Case 2:

If all the elements in the array are negative Arr[] = [-4, -8, -9, -3, -5]

Answer:

Here, since a subarray should contain at least one element, the max subarray would be the element with the max value

Ans: -3

Case 3:

If positives are present in between

Arr[] = [-ve -ve -ve +ve +ve +ve +ve -ve -ve -ve]

Answer:

Here max sum would be the sum of all positive numbers

Case 4:

If all negatives are present either on left side or right side.

Arr[ ] = [-ve -ve -ve +ve +ve +ve +ve]

OR

Arr[ ] = [+ve +ve +ve +ve -ve -ve -ve -ve]

Answer:

All postives on sides

Case 5 :

Hint:

What if it's some ve+ followed by some ve- and then again some more positives...

+ve +ve +ve -ve -ve -ve +ve +ve +ve +ve +ve

Solution:¶

We will take all positives, then we consider negatives only if the overall sum is positive because in the future if positives come, they may further increase this positivity(sum).

Example -

A[ ] = { -2, 3, 4, -1, 5, -10, 7 }

Answer array: 3, 4, -1, 5

Explanation:

3+4 = 7
7 + (-1) = 6 (still positive)
6+5 = 11 (higher than 7)

Dry Run¶

    0   1    2    3  4  5   6  7   8
{ -20, 10, -20, -12, 6, 5, -3, 8, -2 }

i	currSum	maxSum
0	-20	-20	reset the currSum to 0 and do not propagate since adding a negative will make it more negative and adding a positive will reduce positivity of that element.

currSum = 0

i	currSum	maxSum
1	10	10
2	10 + (-20)= -10	10	reset currSum to 0

currSum = 0

i	currSum	maxSum
3	-12	10	reset currSum to 0

currSum = 0

i	currSum	maxSum
4	6	10
5	6 + 5	11
6	6 + 5 - 3 = 8	11	Keep currSum as 8 only since if we find a positive, it can increase the sum

i	currSum	maxSum
7	8 + 8 = 16	16
8	16 - 2 = 14	16	Keep currSum as 8 only since if we find a positive, it can increase the sum

Final maxSum = 16

Question¶

Tell the output of the below example after running the Kadane's Algorithm on that example

A[ ] = { -2, 3, 4, -1, 5, -10, 7 }

Choices

9
7
11
0

Find Maximum Subarray Sum Kadanes Pseudocode¶

Pseudocode¶

int maximumSubarraySum(int[] arr, int n) {
    int maxSum = Integer.MIN_VALUE, currSum = 0;

    for (int i = 0; i <= n - 1; i++) {
        currSum += arr[i];

        if (currSum > maxSum) {
            maxSum = currSum;
        }

        if (currSum < 0) {
            currSum = 0;
        }
    }

    return maxSum;
}

Complexity¶

Time Complexity: O(n)
Space Complexity: O(1)

The optimized method that we just discussed comes under Kadane's Algorithm for solving maximum subarray problem

Problem 2 Perform multiple Queries from i to last index¶

Problem Statement¶

Given an integer array A where every element is 0, return the final array after performing multiple queries

Query (i, x): Add x to all the numbers from index i to N-1

Example

Let's say we have a zero-filled array of size 7 with the following queries:

Query(1, 3)
Query(4, -2)
Query(3, 1)

Let's perform these queries and see how it works out.

Example Explanation

Index	0	1	2	3	4	5	6
Array	0	0	0	0	0	0	0
Q1	:	+3	+3	+3	+3	+3	+3
Q2	:	:	:	:	-2	-2	-2
Q3	:	:	:	+1	+1	+1	+1
Ans[]	0	3	3	4	2	2	2

Question¶

Return the final array after performing the queries

Note:

Query (i, x): Add x to all the numbers from index i to N-1
0-based Indexing

A = [0, 0, 0, 0, 0]
Query(1, 3)
Query(0, 2)
Query(4, 1)

Choices

[6, 6, 6, 6, 6]
[2, 5, 5, 5, 6]
[2, 3, 3, 3, 1]
[2, 2, 5, 5, 6]

Explanation¶

Index	0	1	2	3	4
Array	0	0	0	0	0
Q1	:	+3	+3	+3	+3
Q2	+2	+2	+2	+2	+2
Q3	:	:	:	:	+1
Ans[]	2	5	5	5	6

Perform multiple Queries from i to last index Solution Approaches¶

Brute force Approach¶

One way to approach this question is for a given number of Q queries, we can traverse the entire array each time.

Complexity¶

Time Complexity: O(Q * N)
Space Complexity: O(1)

Optimized Solution¶

Hint:¶

Wherever we're adding the value initially, the value is to be carried forward to the very last of the array isn't it?
Which is the concept that helps us carry forward the sum to indices on right hand side ?

Expected: Prefix Sum!

Idea is that first we add the values at the ith indices as per given queries.
Then, at the end, we can propagate those sum to indices on right.
This way, we're only iterating over the array once unlike before.

Dry Run¶

Index	0	1	2	3	4	5	6
Array	0	0	0	0	0	0	0
Q1	:	+3	:	:	:	:	:
Q2	:	:	:	:	+2	:
Q3	:	:	:	+1	:	:	:
Ans[]	0	3	0	1	2	0	0
psum[]	0	3	3	4	6	6	6

Pseudocode¶

for (i = 0; i < Q.length; i++) {
    index = B[i][0];
    val = B[i][1];
    A[index] += val;
}
for (i = 1; i < N; i++) {
    A[i] += A[i - 1];
}
return A;

Complexity¶

Time Complexity: O(Q + N)
Space Complexity: O(1)

since we are only making changes to the answer array that needs to be returned.

Problem 3 Perform multiple Queries from index i to j¶

Problem Statement¶

Given an integer array A such that all the elements in the array are 0. Return the final array after performing multiple queries

Query: (i, j, x): Add x to all the elements from index i to j

Given that i <= j

Examples

Let's take an example, say we have the zero-filled array of size 7 and the queries are given as q1 = (1, 3, 2) q2 = (2, 5, 3) q3 = (5, 6, -1)

Question¶

Find the final array after performing the given queries on array of size 8.

i	j	x
1	4	3
0	5	-1
2	2	4
4	6	3

Choices

1 2 6 3 5 2 3 0
-1 2 6 2 5 2 3 3
-1 2 6 2 5 2 3 0
1 2 6 3 5 2 0 3

Observations¶

In the provided query format Query: (i, j, x) here, start (i) and end (j) are specifiying a range wherein the values (x) needs to be added to the elements of the given array

Brute force Solution Approach¶

In this solution we can iterate through the array for every query provided to us and perform the necessary operation over it.

Dry Run¶

The provided queries we have are

q1 = (1, 3, 2)
q2 = (2, 5, 3)
q3 = (5, 6, -1)

Index	0	1	2	3	4	5	6
Arr[7]	0	0	0	0	0	0	0
V1		2	2	2
V2			3	3	3	3
V3						-1	-1
Ans	0	2	5	5	3	2	-1

Complexity¶

Time Complexity: O(Q * N)
Space Complexity: O(1)

Optimized Solution¶

This time, wherever we're adding the value initially, the value is to be carried forward only till a particular index, right?
Can we use the Prefix Sum concept here are well ?
How can we make sure that the value only gets added up till index j ?
What can help us negate the effect of +val ?

Idea¶

We can add the value at the starting index and subtract the same value just after the ending index which will help us to only carry the effect of +val till a specific index.
From the index(k) where we have done -val, the effect will neutralise i.e, from (k to N-1)

Pseudocode:¶

zeroQ(int N, int start[], int end[], int val[]) {
    long arr[N] = 0;
    for (int i = 0; i < Q; i++) {

        //ith query information: start[i], end[i], val[i]
        int s = start[i], e = end[i], v = val[i];

        arr[s] = arr[s] + v;

        if (e < n - 1) {
            arr[e + 1] = arr[e + 1] - v;
        }
    }

    //Apply cumm sum a psum[] on arr
    for (i = 1; i < N; i++) {
        arr[i] += arr[i - 1];
    }

    return arr;
}

Complexity¶

Time Complexity: O(Q + N)
Space Complexity: O(1)

Problem Statement

Given N buildings with height of each building, find the rain water trapped between the buildings.

Example Explanation¶

Example:

arr[] = {2, 1, 3, 2, 1, 2, 4, 3, 2, 1, 3, 1}

We now need to find the rainwater trapped between the buildings

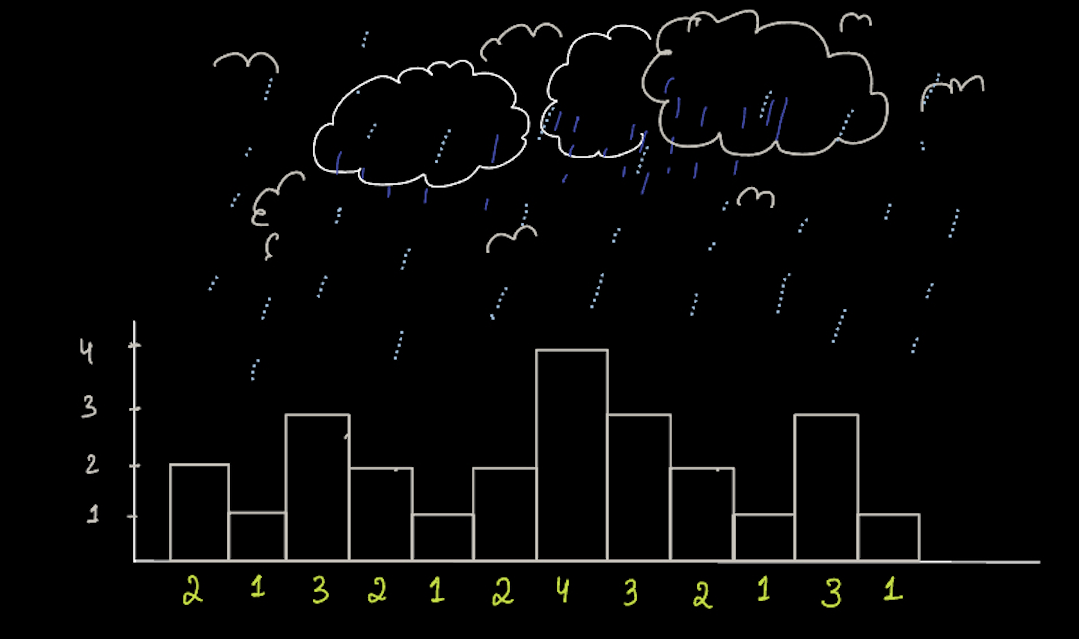
Ans: 8

Hint:¶

If we get units of water stored over every building, then we can get the overall water by summing individual answers.

Observations¶

How much water is stored over building 2 ? -> 4 units

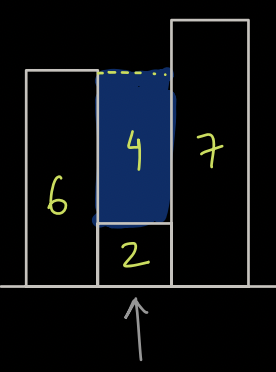
Now, how much water is stored over building 2 ? still -> 4 units

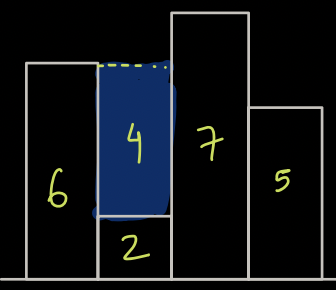
Now, how much water is stored over building 2 ? still -> 4 units

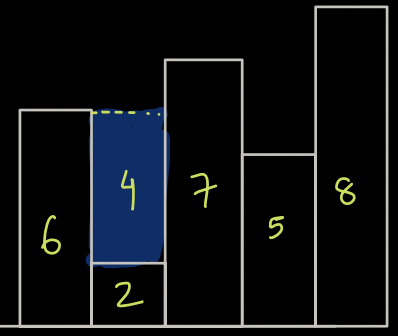
Now, how much water is stored over building 2 ? Now it is 6

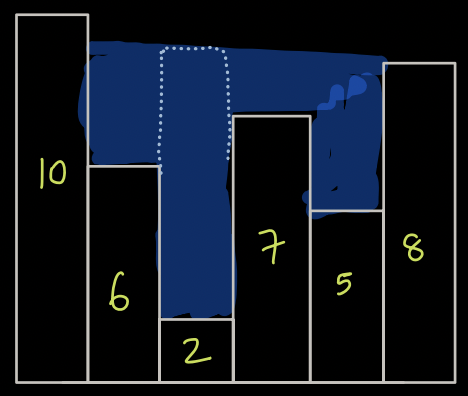
Now, how much water is stored over building 2 ? Now it is 8

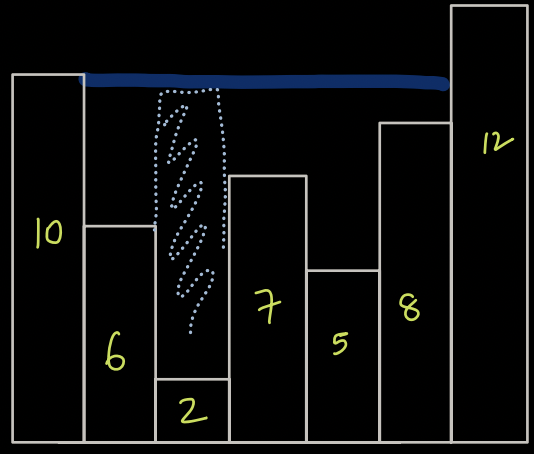
Conclusion:¶

It depends on the height of the minimum of the largest buildings on either sides.

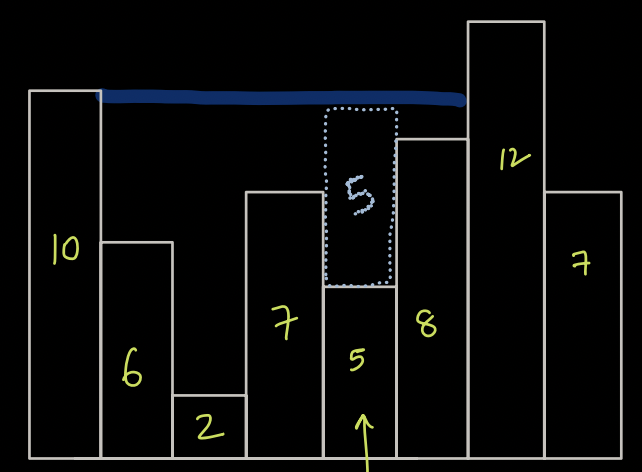
Example:

Water stored over building 5 depends on minimum of the largest building on either sides.

i.e, min(10, 12) = 10

Water stored over 5 is 10 - 5 = 5 units.

Question¶

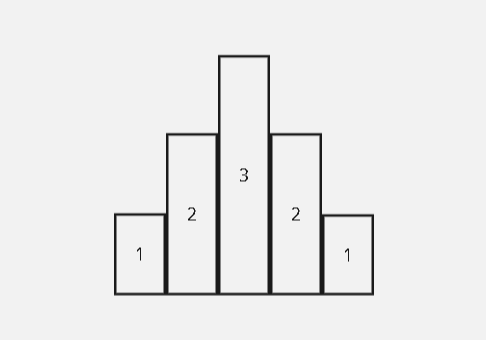
Given N buildings with height of each building, find the rain water trapped between the buildings.

A = [1, 2, 3, 2, 1]

Choices

2
9
0
3

Explanation:

No water is trapped, Since the building is like a mountain.

Warning

Please take some time to think about the solution approach on your own before reading further.....

Rain Water Trapping Brute Force Approach¶

For ith building,
We need to find maximum heights on both the left and right sides of ith building.

NOTE: For 0^th and (N-1)th building, no water will be stored on top.

Pseudocode (Wrong)¶

ans = 0

for (int i = 1; i < N - 1; i++) {
    maxL = max(0 to i - 1); //loop O(N)
    maxR = max(i + 1 to N - 1); //loop O(N)

    water = min(maxL, maxR) - A[i];
    ans += water;
}

Edge Case¶

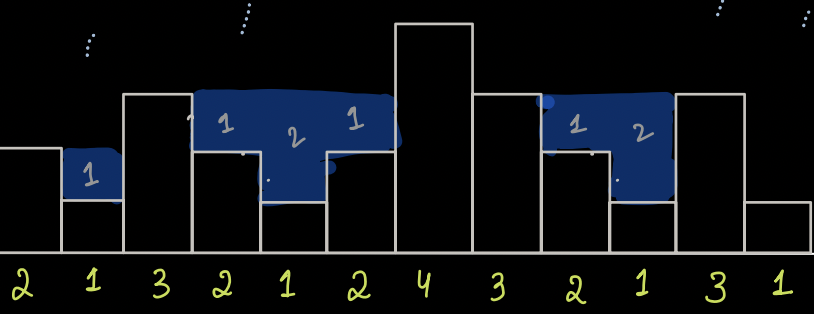
For building with height 4, the Lmax = 3 and Rmax = 3

min(3, 3) = 3

water = 3 - 4 < 0

So, for such case, we'll take water stored as 0.

Pseudocode (Correct)¶

ans = 0

for (int i = 1; i < N - 1; i++) {
    maxL = max(0 to i - 1); //loop O(N)
    maxR = max(i + 1 to N - 1); //loop O(N)

    water = min(maxL, maxR) - A[i];

    if (water > 0) {
        ans += water;
    }
}

Complexity¶

Time Complexity: O(N^2)

{Since for every element, we'll loop to find max on left and right}

Space Complexity: O(N)

Rain Water Trapping Optimised Approach¶

We can store the max on right & left using carry forward approach.

We can take 2 arrays, lmax[] & rmax[].
Below is the calculation for finding max on left & right using carry forward approach.
This way, we don't have to find max for every element, as it has been pre-calculated.

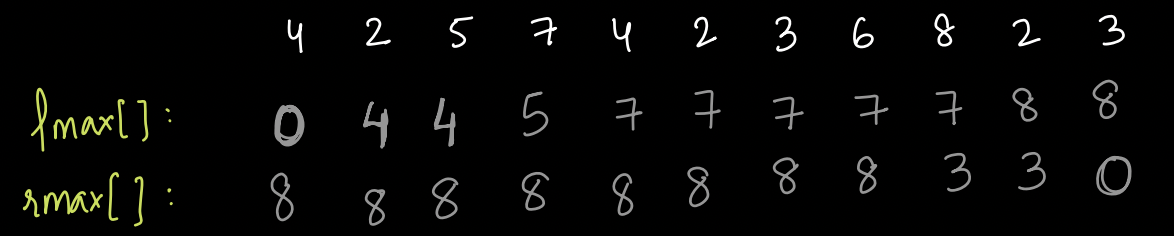
Pseudocode¶

ans = 0;

int lmax[N] = {
    0
};
for (int i = 1; i < N; i++) {
    lmax[i] = max(lmax[i - 1], A[i - 1]);
}

int rmax[N] = {
    0
};
for (int i = N - 2; i >= 0; i--) {
    rmax[i] = max(rmax[i + 1], A[i + 1]);
}

for (int i = 1; i < N - 1; i++) {
    water = min(lmax[i], rmax[i]) - A[i];

    if (water > 0) {
        ans += water;
    }
}

Complexity¶

Time Complexity: O(N)

{Since we have precalculated lmax & rmax}

Space Complexity: O(N)