Queues: Implementation & Problems¶

Queue¶

A queue represents a linear data structure where items are added at one end and removed from the other end. It follows the "First-In-First-Out" (FIFO) principle, meaning that the item that has been inserted first in queue will be the first one to be removed. To illustrate this concept, let's use a ticket counter as an example.

Example: Ticket Counter Queue

Imagine you're at a ticket counter for a popular event, and there are several people waiting in line to purchase tickets. This line of people forms a queue, and the first person who has come in this line will get the ticket first.

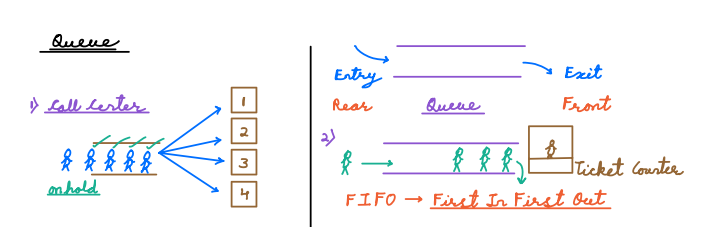
Common operations in a queue include:

Enqueue:
This operation adds an element to the back (or rear) of the queue. It is also called "push" in some contexts.
Dequeue:
This operation removes and returns the element from the front of the queue. It is also called "pop" in some contexts.
Peek or Front:
This operation allows you to look at the element at the front of the queue without removing it. It is useful for inspecting the next item to be processed.
IsEmpty:
This operation checks if the queue is empty. If it's empty, it means there are no elements in the queue.
Size or Length:
This operation returns the number of elements currently in the queue. It provides the count of items in the queue.

Q. Can a stack or queue have a limit of elements it can have, and then we can use isFull()?

Sol. Yes, both stacks and queues can have a limit on the number of elements they can hold, and you can use an "isFull()" method to check if they have reached their capacity. This concept is commonly referred to as a "bounded" stack or queue.

title: Implementaion of queue
description: Discussion about the various concepts related to implementaion of queue in detail.
duration: 2100

Implementaion of Queue¶

Here's how you can implement a queue using a dynamic array along with pseudocode for the enqueue, dequeue, and isEmpty operations:

Queue using Dynamic Array:

- Initialize an empty dynamic array (e.g., ArrayList or Python list) to store the elements.
- Initialize two pointers: 'front' and 'rear'. Initially, both are set to -1.

Pseudocode for Enqueue (Add an element to the rear of the queue):

enqueue(element):
    if rear is -1:
        # Empty queue, set both front and rear to 0
        set front and rear to 0
    else if rear is at the end of the array:
        # Check if there is space for expansion
        if front > 0:
            # Move elements to the beginning of the array
            for i from front to rear:
                array[i - front] = array[i]
            set rear to (rear - front)
            set front to 0
        else:
            # If no space, resize the array by creating a new larger array
            new_size = current_array_size * 2  # You can choose your resizing strategy
            create a new array of size new_size
            copy elements from the current array to the new array
            set array to new_array
            set rear to (rear - front)
            set front to 0


    array[rear] = element
    increment rear by 1

Pseudocode for Dequeue (Remove an element from the front of the queue):
dequeue():
    if front is -1:
        # Empty queue, nothing to dequeue
        return "Queue is empty"
    else:
        element = array[front]
        increment front by 1
        if front > rear:
            # Reset front and rear to -1 if the queue is empty
            set front and rear to -1
        return element

Pseudocode for isEmpty (Check if the queue is empty):
isEmpty():
    if front is -1:
        return true
    else:
        return false

This pseudocode provides a basic implementation of a queue using a dynamic array. It handles the enqueue and dequeue operations efficiently by resizing the array when necessary to accommodate more elements. The isEmpty function checks if the queue is empty by examining the state of the front pointer.

Implementation of Queues using linkedlist¶

Insert at Head (prepend):
Time Complexity: O(1)
Explanation: Inserting a node at the head of a singly linked list involves creating a new node, setting its next pointer to the current head, and updating the head pointer to the new node. This operation takes constant time because it doesn't depend on the size of the list.
Insert at Tail (append):
Time Complexity: O(n)
Explanation: To insert a node at the tail of a singly linked list, you typically need to traverse the entire list to find the current tail node. This operation takes linear time since you have to visit each node in the list to reach the end.
Delete at Head:
Time Complexity: O(1)
Explanation: Deleting a node at the head of a singly linked list is a constant-time operation. You simply update the head pointer to point to the next node in the list.
Delete at Tail:
Time Complexity: O(n)
Explanation: Deleting a node at the tail of a singly linked list also requires traversing the entire list to find the current tail node. This operation takes linear time since you have to reach the end of the list to perform the deletion.

Queue functionality can be achieved by using two of the methods mentioned:

Insertion at Head and Deletion at tail:
This approach can be used to provide the functionality of queue.Elements are inserted at the head (enqueue operation)with TC O(1) and removed from the tail with TC O(n)(dequeue operation). This ensures that the first element added to the queue is the first one to be removed.
Insertion at Tail and Deletion at Head:
This approach can also be used to create a queue using LinkedList.Elements are inserted at tail with TC O(n) and removed from the head with TC O(1). We can optimise the TC of insertion at tail to O(1) by maintaining a tail pointer and this is why we generally used this approach for queue creation through LinkedList.

Question¶

What will be the state of the queue after these operations

enqueue(3), enqueue(7), enqueue(12), dqueue(), dqueue(), enqueue(8), enqueue(3)

Choices

12, 8, 3
3, 7, 12, 8
3, 8, 3
7, 12, 3

Explanation

Let's break down the sequence of queue operations:

enqueue(3) : Queue becomes [3]
enqueue(7) : Queue becomes [3, 7]
enqueue(12) : Queue becomes [3, 7, 12]
dequeue() : Removes the element from the front, and the queue becomes [7, 12]
dequeue() : Removes the element from the front, and the queue becomes [12]
enqueue(8) : Queue becomes [12, 8]
enqueue(3) : Queue becomes [12, 8, 3]

So, after these operations, the final state of the queue is [12, 8, 3]

Question¶

What will be the state of the queue after these operations

enqueue(4), dqueue(), enqueue(9), enqueue(3), enqueue(7), enqueue(11), enqueue(20), dqueue()

Choices

4, 9, 3, 7
3, 7, 11, 20
9, 3, 7, 11
3, 7, 20

Explanation

Let's go through the sequence of queue operations:

enqueue(4): Queue becomes [4]
dequeue(): Removes the element from the front, and the queue becomes empty.
enqueue(9): Queue becomes [9]
enqueue(3): Queue becomes [9, 3]
enqueue(7): Queue becomes [9, 3, 7]
enqueue(11): Queue becomes [9, 3, 7, 11]
enqueue(20): Queue becomes [9, 3, 7, 11, 20]
dequeue(): Removes the element from the front, and the queue becomes [3, 7, 11, 20]

So, after these operations, the final state of the queue is [3, 7, 11, 20]

Implementaion of queue using Stack¶

The explaination for implementing a queue using two stacks step by step:

class QueueUsingTwoStacks {
private:
    std::stack<int> stack1;  // For enqueue operations
    std::stack<int> stack2;  // For dequeue operations

We define a C++ class called QueueUsingTwoStacks. This class has two private member variables: stack1 and stack2. stack1 is used for enqueue operations, and stack2 is used for dequeue operations.

public:
    void enqueue(int value) {
        // Simply push the value onto stack1
        stack1.push(value);
    }

The enqueue method allows you to add an element to the queue. In this implementation, we simply push the given value onto stack1, which represents the back of the queue.

    int dequeue() {
        if (stack2.empty()) {
            // If stack2 is empty, transfer elements from stack1 to stack2
            while (!stack1.empty()) {
                stack2.push(stack1.pop());
            }
        }

        // Pop the front element from stack2 (which was originally at the front of stack1)
        if (!stack2.empty()) {
            int front = stack2.top();
            stack2.pop();
            return front;
        }

        // If both stacks are empty, the queue is empty
        std::cerr << "Queue is empty" << std::endl;
        return -1;  // You can choose a different sentinel value or error handling strategy
    }

The dequeue method allows you to remove and return the front element from the queue. Here's how it works:

If stack2 is empty (meaning we haven't yet transferred elements from stack1 to stack2), we perform the transfer. We pop elements from stack1 and push them onto stack2, effectively reversing the order of elements. This is done to ensure that the front element is at the top of stack2.
We then pop the top element from stack2 (which was originally at the front of the queue) and return it.
If both stack1 and stack2 are empty, we print an error message and return a sentinel value (-1 in this case) to indicate that the queue is empty. You can customize the error handling strategy as needed.

    bool isEmpty() {
        return stack1.empty() && stack2.empty();
    }
};

The isEmpty method checks whether the queue is empty. It returns true if both stack1 and stack2 are empty, indicating that there are no elements in the queue.

In the main function, we create an instance of QueueUsingTwoStacks, perform enqueue and dequeue operations, and check if the queue is empty. The example code demonstrates the usage of this queue implementation.

Problem 1 Nth perfect number¶

Write a function findNthPerfectNumber(N) that takes an integer N as input and returns the Nth perfect number formed by the only digits 1 and 2.

Input:

An integer \(N (1 <= N <= 1000)\), representing the position of the desired perfect number.

Output:

Return the Nth perfect number formed using only digits 1 and 2.

Example:

Question Explanation

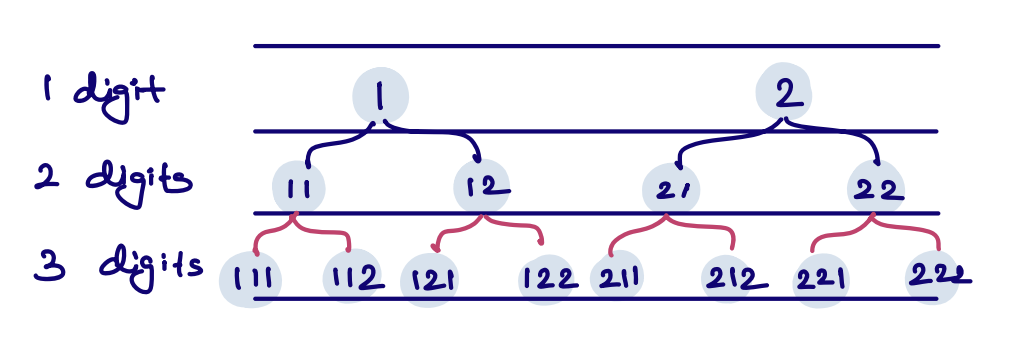
As we can see in above example, we have to insert 1 and 2 in the queue.
The next numbers can be made using the previous digits by appending the combination of 1 and 2.
Like to get 11 we append 1 after 1, to get 12 we append 2 after 1.
Similarly, we can generate numbers 21 by appending 1 after 2, and to get the 22, we can append 2 to 2 and so on.
As we have to append and remove digits frequently so queue can help us here.

Question¶

What is the 5^th perfect number formed by the only digits 1 and 2.

Choices

11111
22222
21
12

Explanation:

From the image, the 5^th Perfect Number is 21.

Nth perfect number Solution¶

Solution¶

int solve(N) {
    if (N <= 2) return N
    // Queue ->q    
    q.enqueue(1) q.enqueue(2)
    i = 3
    while (i <= N) {
        x = q.dequeue()
        a = x * 10 + 1
        b = x * 10 + 2 //a + 1
        if (i == N) return a
        if (i + 1 == N) return b
        q.enqueue(a)
        q.enqueue(b)
        i = i + 2
    }
}

Dry Run¶

To dry run the provided code for N = 10, we'll create a table to keep track of the values of q (the queue) and i at each step.

|  N  |  q   | i   |                   |
|:---:|:----:| --- |:-----------------:|
| 10  | 1, 2 | 3   | // Initial values |

// Loop starts

|   N   |    q           |   i |
|-------|----------------|-----|
|  10   |  2, 11, 12     |  3  |// Dequeue 1, enqueue 11 and 12
|  10   | 11, 12,21,22   |  5  |// Dequeue 2, enqueue 21 and 22
|  10   |12,21,22,111,112|  7  |// Dequeue 11, enqueue 111 and 112
|  10   |21,22,111,112,121,122|  9  |// Dequeue 12, enqueue 121 and 122

// Now Loop ends at N == 10 , and ans = 122

The function dequeues and enqueues values in the queue until i reaches N. When i equals N, it returns the current value of a. In this case, for N = 10, the function returns 112.

Complexity¶

Time Complexity: O(n)

Space Complexity: O(n)

Doubly Ended Queue¶

A double-ended queue (deque) is a data structure that allows elements to be added or removed from both ends, making it versatile for various operations. A double-linked list is a common choice for implementing a deque because it provides efficient operations for adding and removing elements from both ends.

Here are some basic operations that are possible with a doubly-ended queue implemented using a double-linked list:

Insertion at Front (push_front): Add an element to the front (head) of the deque.
Insertion at Back (push_back): Add an element to the back (tail) of the deque.
Removal from Front (pop_front): Remove and return the element from the front of the deque.
Removal from Back (pop_back): Remove and return the element from the back of the deque.
Front Element Access (front): Get the element at the front of the deque without removing it.
Back Element Access (back): Get the element at the back of the deque without removing it.

A double-linked list is well-suited for implementing a deque because it allows for efficient insertions and removals at both ends. Each node in the linked list has pointers to the next and previous nodes, making it easy to manipulate the list in both directions.

Problem 2 Sliding Window Maximum¶

Problem Statement¶

Given an integer array A and an window of size k find the max element.

Input

An integer array A and integer k .

Output

An integer representing the maximum length of a subarray of A in which the average of all elements is greater than or equal to k. If no such subarray exists, return 0.

Example

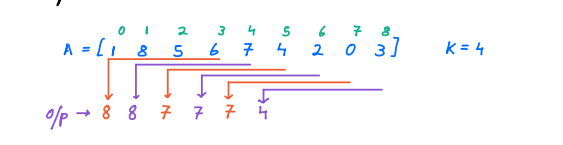
Question Explanation¶

Find max elements in 4-element sliding windows of array A:

[1, 8, 5, 6] -> max: 8
[8, 5, 6, 7] -> max: 8
[5, 6, 7, 4] -> max: 7
[6, 7, 4, 2] -> max: 7
[7, 4, 2, 0] -> max: 7
[4, 2, 0, 3] -> max: 4

Result: [8, 8, 7, 7, 7, 4].

Initialize an empty list max_elements.
Iterate from index 0 to 3 (inclusive) to create windows of size 4.
Find the maximum element in each window and append it to max_elements.
Result: [8, 8, 7, 7, 7, 4], representing max elements in each 4-element window in A.

Question¶

Given an integer array A and an window of size k find the max element.

A = [1, 4, 3, 2, 5]
k = 3

Choices

[4, 4, 5]
[5, 5, 5]
[1, 4, 3]
[5, 4, 3]

Explanation:

Maximum of [1, 4, 3] is 4
Maximum of [4, 3, 2] is 4
Maximum of [3, 2, 5] is 5

So, [4, 4, 5] is the answer.

Warning

Please take some time to think about the solution approach on your own before reading further.....

Sliding Window Maximum Approaches¶

Brute Force Approach¶

Brute-force approach to find max element in a window of size k in array A involves iterating through windows, finding max within each, and storing results. Time complexity: O(n * k) and space complexity: O(1).

Dry Run using the Sliding Window Approach¶

Array A = [1, 8, 5, 6, 7, 4, 2, 0, 3] and k = 4.

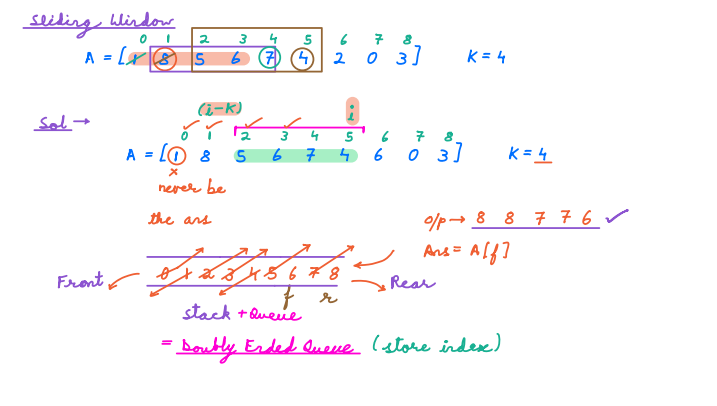
Let's dry run the code with the given example:

Array A = [1, 8, 5, 6, 7, 4, 2, 0, 3] and k = 4.

Initialize an empty queue q.
Start iterating through the array elements.
For i = 0, A[i] = 1: - Queue q is empty, so nothing happens. - Enqueue i at the rear of the queue. q = [0].
For i = 1, A[i] = 8: - The front element of the queue is at index 0, which is smaller than the current element and thus can't be the maximum for any window. - Deque the element and Enqueue i at the rear of the queue. q = [1].
For i = 2, A[i] = 5: - q is not empty, and A[r] (element at index 1) is greater than A[i], so we don't do anything. - Enqueue i at the rear of the queue. q = [2].
For i = 3, A[i] = 6: - q is not empty, and A[r] (element at index 2) is smaller than A[i], so we deque it, now 8 is greater than 6 so don't do anything. - Enqueue i at the rear of the queue. q = [3].

After the first K insertions, the q = [8,6]; Now the maximum of this window is present in the front so print it and slide the window. To slide the window, check if A[i - k] is present in front, if yes then dequeue it. Add the next element to slide the window

Continue this process for the remaining elements.
The final output will be the maximum elements in each group of size k:
For k = 4, the maximum elements are [8, 8, 7, 7, 4, 2, 3].

So, the dry run demonstrates how the code finds and prints the maximum elements in groups of size k as it iterates through the array.

Pseudocode (Using Dequeue)¶

function findMaximumInGroups(A, k):
    Initialize an empty queue q
    n = length(A)  // Total number of elements in the array A

    for i from 0 to k - 1:
        while (!q.isEmpty() and A[i] >= A[q.rear()]):
            q.dequeueRear() // Remove elements that are smaller than A[i]
        q.enqueueRear(i) // Add the current element to the queue

    print A[q.front()] // Print the maximum element in the current group

    // Slide for next windows

    for i from k to n - 1:
        if (!q.isEmpty() and q.front() == i - k):
            q.dequeueFront() // Remove elements that are outside the current window

        while (!q.isEmpty() and A[i] >= A[q.rear()]):
            q.dequeueRear() // Remove elements that are smaller than A[i]
        q.enqueueRear(i) // Add the current element to the queue

    print A[q.front()] // Print the maximum element in the last group

# Example usage:

A = [1, 8, 5, 6, 7, 4, 2, 0, 3] 
k = 4
findMaximumInGroups(A, k)

Complexity¶

Time Complexity: O(n)
Space Complexity: O(n)