Recursion 2¶
Question¶
What is the output of the following code for N = 3?
void solve(int N){
if(N == 0)
return;
solve(N-1);
print(N);
}
Choices
- 1 2 3
- 0 1 2
- 2 1 0
- 3 2 1
void solve(int N) {
if (N == 0)
return;
solve(N - 1);
print(N);
}
N=3
- So first of all, solve(3) is called,
- Then solve(3) will first call for solve(2) as n!=0,
- Similarly, solve(2) calls for solve(1), and then solve(1) calls for solve(0).
Now n==0 so return.
Then solve(1) will print 1, then it will return, and after that solve(2) will print 2, in this way 1, 2, 3 will be printed as an output.
Question¶
What is the output of the following code for N = 3?
void solve(int N){
if(N == 0)
return;
print(N);
solve(N-1);
}
Choices
- 1 2 3
- 0 1 2
- 2 1 0
- 3 2 1
void solve(int N){
if(N == 0)
return;
print(N);
solve(N-1);
}
N=3
- So first of all, solve(3) is called,
- Then solve(3) will first print 3, then call for solve(2) as n!=0,
- In this way solve(2) first print 2, then call for solve(1), and then solve(1) will print 1, then call for solve(0).

Now n==0 so return.
Then solve(1) will return, after that solve(2) will return.
In this way 3, 2, 1 will be printed as an output.
Question¶
What is the output of the following code for N = -3?
void solve(int N){
if(N == 0)
return;
print(N);
solve(N-1);
}
Choices
- -3 -2 -1
- 3 2 1
- Error; Stack Overflow
- 1 2 3
void solve(int N){
if(N == 0)
return;
print(N);
solve(N-1);
}
N = -3
In this question we will never reach 0, that's why we are getting stack overflow.
At first solve(-3) is called, then it will print -3
call for solve(-4), then it will print -4
call for solve(-5), in this way, it will keep making calls infinitely, as we will not reach zero, hence stack overflow error occurs.
Problem 1 Power Function¶
Problem Statement
Given two integers a and n, find an using recursion.
Input
a = 2
n = 3
Output
8
Explanation
23 i.e, 2 * 2 * 2 = 8.
Warning
Please take some time to think about the recursive approach on your own before reading further.....
Brute Force Approach¶
The above problem can be redefined as:
a ^ n = a * a * a......* a (n times).
The problem can be broken into subproblem as:
a ^ n = a ^ (n-1) * a
So we can say that pow(a,n) is equivalent to
pow(a,n) = pow(a,n-1) * a
Here, pow(a,n) is the defined as a^n.
We have seen how the problem is broken into subproblems. Hence, it can be solved using recursion.
Below is the algorithm:
- Assumption step:
- Define a recursive function pow(a,n).
- Main Logic:
- Define a recursive case: if n > 0, then calculate the pow(a,n-1).
- Return a * pow(a,n-1).
- Base Case:
- Base condition: if n = 0, then return 1.
Pseudocode¶
function pow(int a, int n) {
if (n == 0) return 1;
return a * pow(a, n - 1);
}
Complexity¶
We shall calculate Time Complexity at the end.
Power Function Optimized Approach 1¶
We can also divide pow(a, n) as follows:
if n is even:
pow(a,n) = pow(a,n/2) * pow(a,n/2)
if n is odd:
pow(a,n) = pow(a,n/2) * pow(a,n/2) * a
Recursion Steps:¶
- Assumption Step:
- Define a recursive function pow(a,n).
- Main Logic:
- if n is odd, then return pow(a,n/2) * pow(a,n/2) * a.
- else return pow(a,n/2) * p(a,n/2).
- Base Condition:
- if n is equal to 0, then return 1.
Pseudocode¶
Function pow(int a, int n) {
if (n == 0) return 1;
if (n % 2 == 0) {
return pow(a, n / 2) * pow(a, n / 2);
} else {
return pow(a, n / 2) * pow(a, n / 2) * a;
}
}
The above function will have more time complexity due to calling the same function twice. We will see it while calculating Time Compleixity.
Time Complexity of Power Function¶
Pseudocode¶
Function pow(int a, int n) {
if (n == 0) return 1;
if (n % 2 == 0) {
return pow(a, n / 2) * pow(a, n / 2);
} else {
return pow(a, n / 2) * pow(a, n / 2) * a;
}
}
Let Time taken to calculate pow(a,n) = f(n).
T(n) = 2 * T(n/2) + 1
Substituting the value of T(n/2) = 2 * T(n/4) + 1
T(n) = 2 * [2 * T(n/4) + 1] + 1
= 4 * T(n/4) + 3
= 2^2 * T(n/2^2) + (2^2 - 1)
Substituting the value of T(n/4) = 2 * T(n/8) + 1
T(n) = 4 * [2 * T(n/8) + 1] + 3
= 8 * T(n/8) + 7
= 2^3 * T(n/2^3) + (2^3 - 1)
Substituting the value of T(n/8) = 2 * T(n/16) + 1
T(n) = 8 * [ 2 * T(n/16) + 1] + 7
= 16 * T(n/16) + 15
= 2^4 * T(n/2^4) + (2^4 - 1)
After, say, k iterations, we shall reach the base step. The equation will be:
T(n) = 2^k * T(n/2^k) + (2^k - 1)
The base case shall take contant time:
T(0) = O(1) or T(1) will also be constant
n/(2 ^ k) = 1
n = 2^k
k = log2(n)
Hence we can say that
T(n) = n * T(1) + (n - 1)
= O(n)
Let's see time complexity of the optimised pow function.
Power Function Optimized Approach - Fast Power¶
In above approach, we are calling function pow(a, n/2) twice. Rather, we can just call it once and use the result twice.
Below is the algorithm:
- Assumption Step:
- Define a recursive function pow(a,n).
- Main Logic:
- Calculate pow(a,n/2) and store it in a variable p.
- if n is odd, then return p * p * a.
- else return p * p.
- Base Condition:
- if n = 0, then return 1.
Pseudocode¶
Function pow(int a, int n) {
if (n == 0) return 1;
int p = pow(a, n / 2);
if (n % 2 == 0) {
return p * p;
} else {
return p * p * a;
}
}
Note: The above function is known as Fast Power or Fast Exponentiation.
Time Complexity of Fast Power¶
Pseudocode¶
Function pow(int a, int n) {
if (n == 0) return 1;
long p = pow(a, n / 2);
if (n % 2 == 0) {
return p * p;
} else {
return p * p * a;
}
}
Let time taken to calculate pow(a,n) = f(n).
Recurrence Relation is:
T(n) = T(n/2) + 1
Substituting the value of T(n/2) = T(n/4) + 1
T(n) = [T(n/4) + 1] + 1
= T(n/4) + 2
Substituting the value of T(n/4) = T(n/8) + 1
T(n) = [T(n/8) + 1] + 2
= T(n/8) + 3
Substituting the value of T(n/8) = T(n/16) + 1
T(n) = [T(n/16) + 1] + 3
= T(n/16) + 4
After say k iterations, we shall reach to the base step.
The equation will be:
T(n) = T(n/2^k) + k
Base case shall take constant time:
T(0) = O(1) or T(1) will also be constant
n/(2 ^ k) = 1
n = 2^k
k = log2(n)
Hence we can say that
T(n) = T(1) + log2(n)
= O(log2(n))
Question¶
How many recursive call in the FAST pow(2,5)?
Choose the correct answer
Choices
- 0
- 2
- 4
- 5
This is ~ log N calls.
Therefore, time complexity of sum of digits = O(log N) * 1 = O(log N)
Space Complexity of pow(a,n)¶
There are total log2(N) recursive calls as shown below:
pow(a,0)
pow(a,1)
pow(a,2)
pow(a,4)
---------------
---------------
---------------
sumofdigits(a,N/2)
sumofdigits(a,N)
Hence, the total O(log2(N)) space required to execute all the recursive calls.
Problem 2 Tower of Hanoi¶
There are n disks placed on tower A of different sizes.
Goal
Move all disks from tower A to C using tower B if needed.
Constraint
- Only 1 disk can be moved at a time.
- Larger disk can not be placed on a small disk at any step.
Print the movement of disks from A to C in minimum steps.
Example 1
Input: N = 1
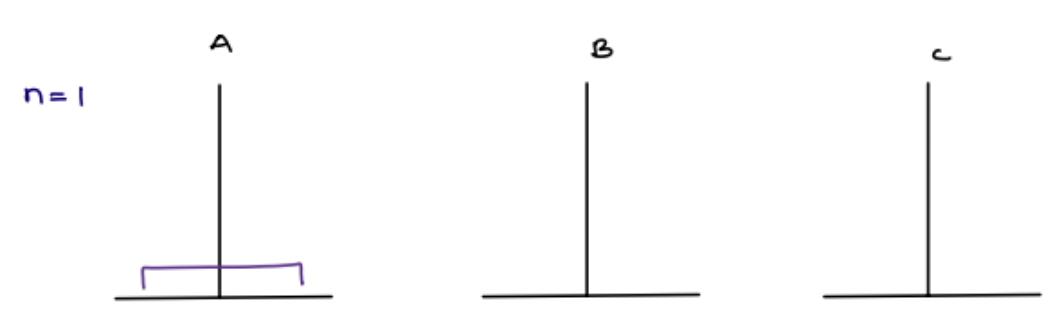
Explanation:
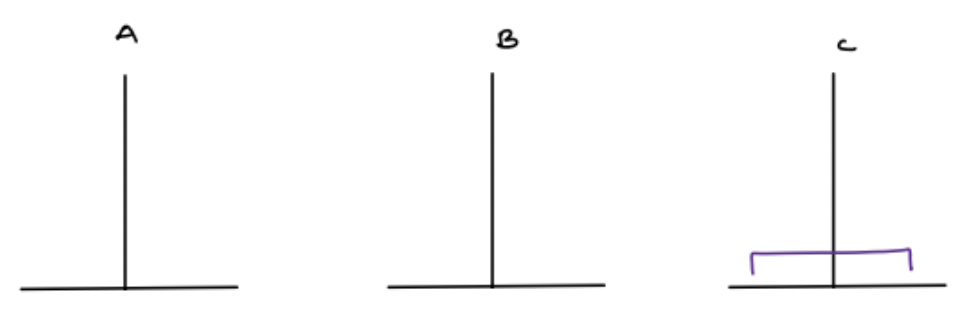
Output:
1: A -> C
Example 2
Input: N = 2
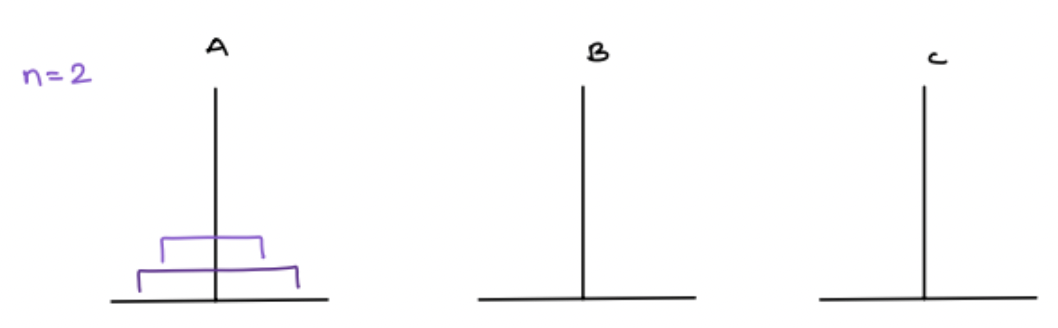
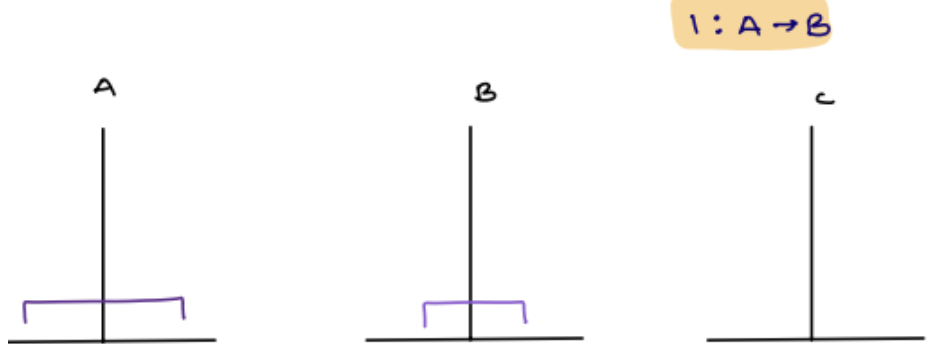
Explanation:
1: A -> B
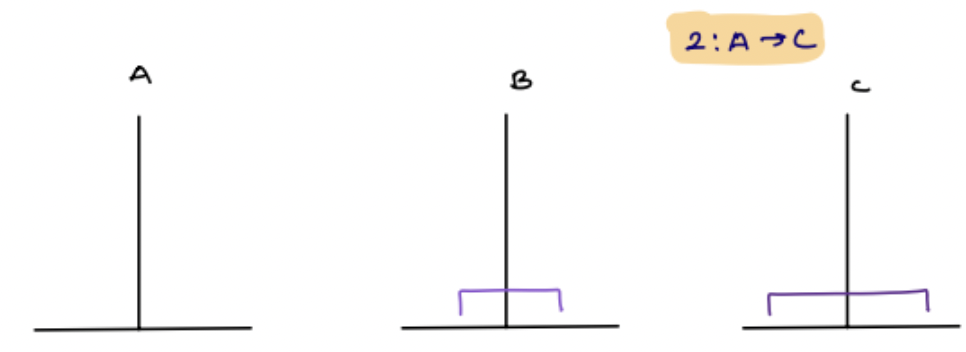
2: A -> C
1: B -> C
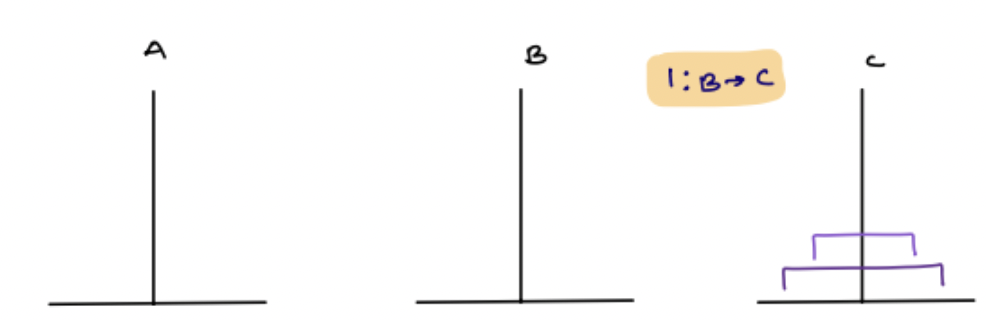
Output:
1: A -> B
2: A -> C
1: B -> C
Example 3
Input: N = 3
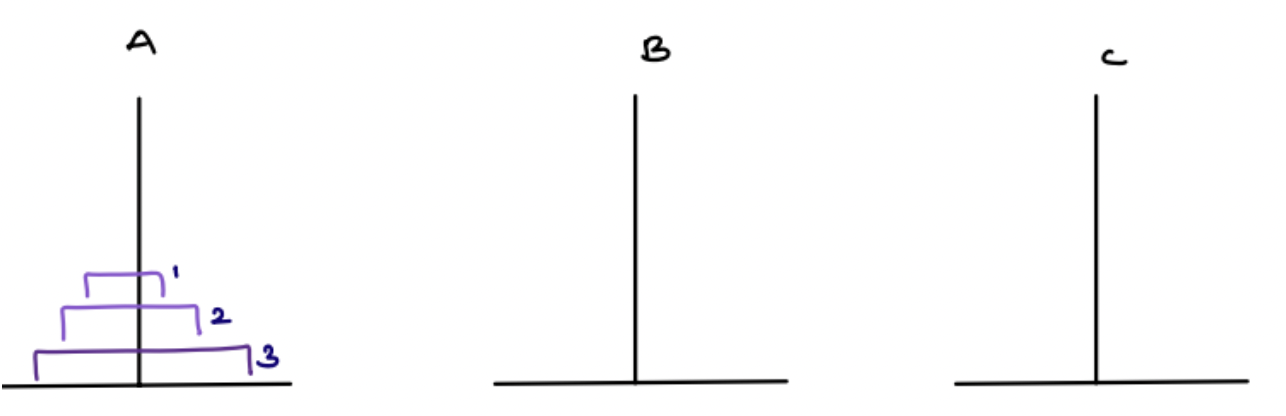
Explanation:
1: A -> C
2: A -> B
1: C -> B
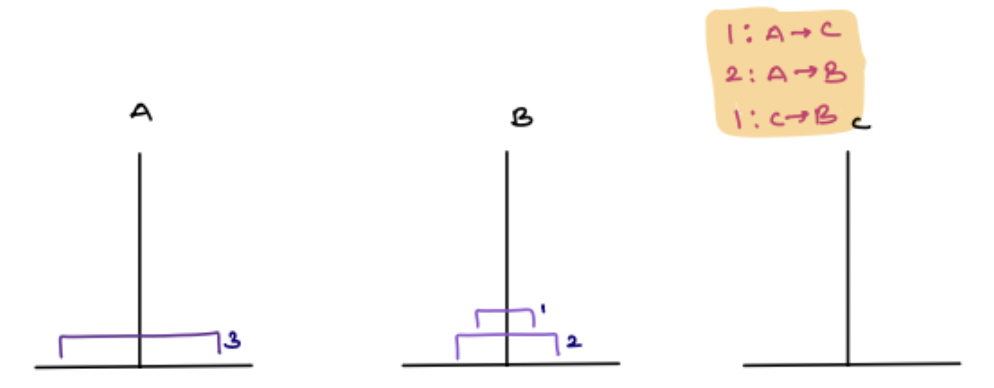
3: A -> C
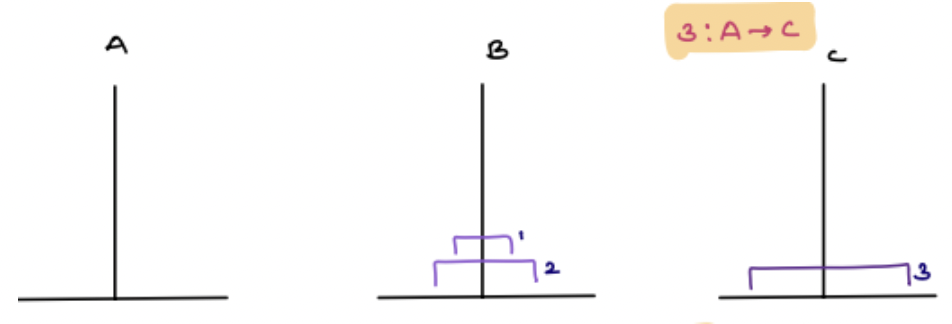
1: B -> A
2: B -> C
1: A -> C
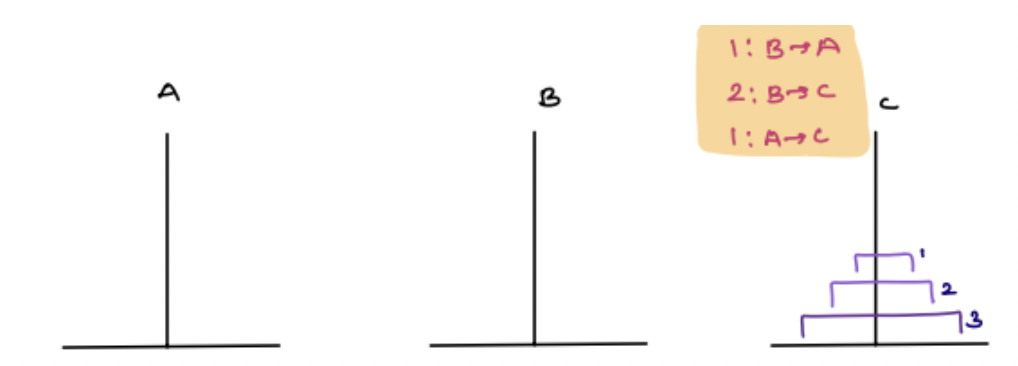
Output:
1: A -> C
2: A -> B
1: C -> B
3: A -> C
1: B -> A
2: B -> C
1: A -> C
n disks¶
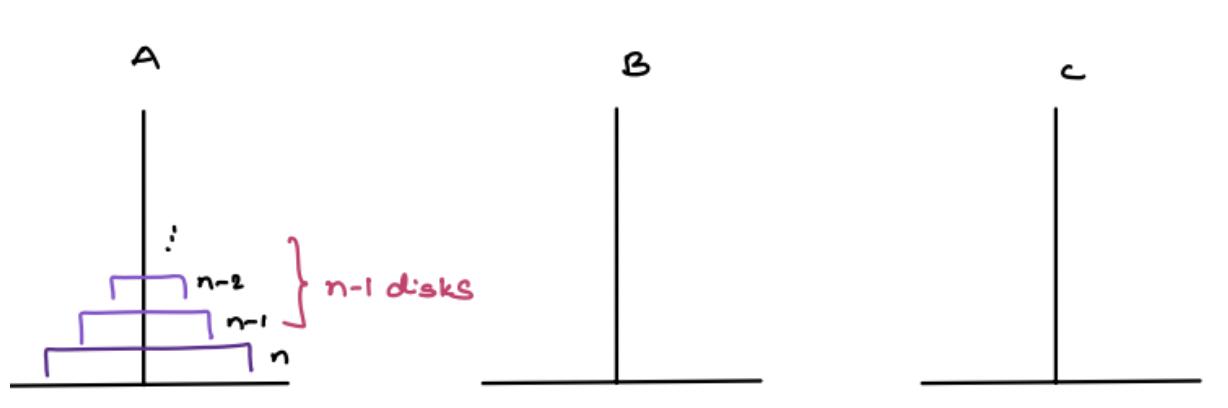
Step 1:
Move (n-1) disks from A to B
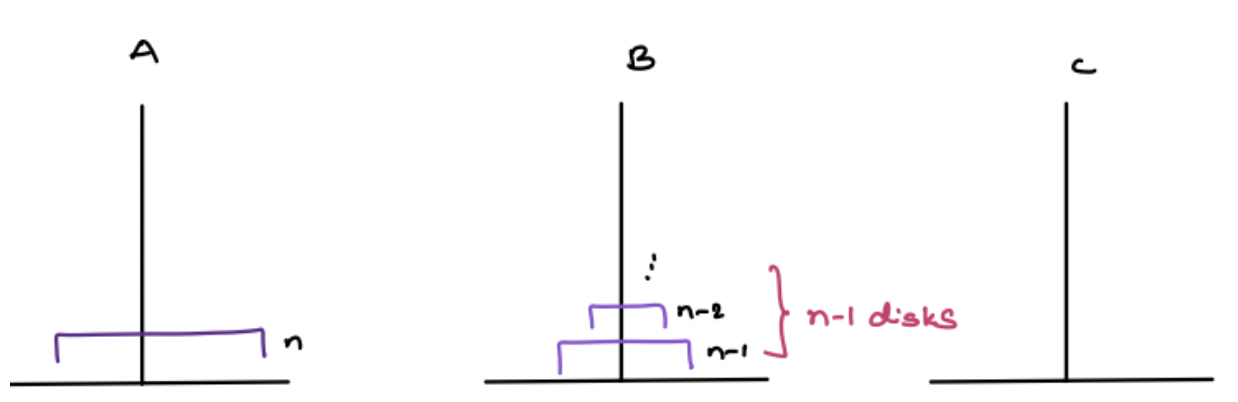
Step 2:
Move n disk to C
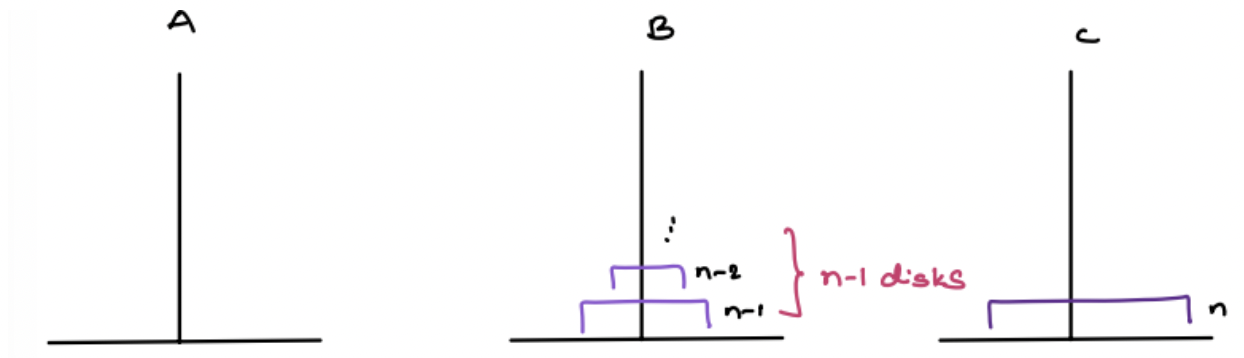
Step 3:
Move (n-1) disks from B to C
Pseudocode¶
src temp dest
void TOH(int n, A, B, C){
1. if(n == 0)
return;
2. TOH(n - 1, A, C, B); // move n-1 disks A->B
3. print(n : A -> C); // moving n disk A->C
4. TOH(n - 1, B, A, C); // move n-1 disks B->C
}
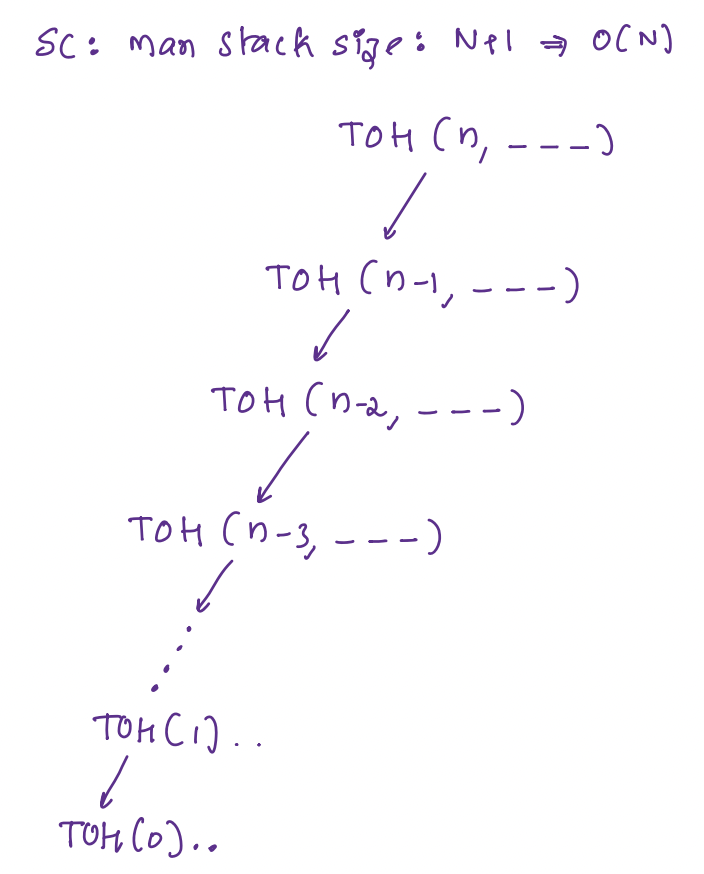
Dry Run¶
n = 3


Output:
1: A -> C
2: A -> B
1: C -> B
3: A -> C
1: B -> A
2: B -> C
1: A -> C
Time Complexity¶
It can be observed in terms of number of steps taken for N

Space Complexity¶