Recursion 1¶

Introduction to Recursion¶

Definition¶

See this video - LINK
Function calling itself.
A problem is broke into smaller problem(subproblem) and the solution is generated using the subproblems.

Example

Here's an example of how recursion can be used to calculate the sum of the first N natural numbers:

sum(N) = 1 + 2 + 3 + 4 + ..... + N-1 + N
sum(N) = sum(N-1) + N

Here, sum(N-1) is smaller instance of same problem that is sum(N). sum(N-1) is known as a subproblem.

How to write a recursive code?¶

We can solve any recursive problem using below magic steps:

Assumptions: Decide what the function does for the given problem.
Main logic: Break the problem down into smaller subproblems to solve the assumption.
Base case: Identify the inputs for which we need to stop the recursion.

Function Call Tracing¶

Function call tracing involves tracing the sequence of function calls that are made when a program is executed.
It involves keeping track of the function calls, their arguments, and the return values in order to understand the flow of the program and how the functions are interacting with each other.

Example:¶

We have the following code:

int add(int x, int y) {
    return x + y;
}

int mul(int x, int y, int z) {
    return x * y * z;
}

int sub(int x, int y) {
    return x - y;
}

void(int x) {
    cout << x << endl;
}

int main() {
    int x = 10;
    int y = 20;
    print(sub(mul(add(x, y), 30), 75));
    return 0;
}

Here are the steps involved in function call tracing of the above code:

We start with the call to sub(mul(add(10, 20), 30), 75).
That called: mul(add(10, 20), 30).
That called: add(10, 20).
add will return 10+20 = 30 to mul function.
mul will return 30*30 = 900 to sub function.
sub will return 900-75 = 825 to print function.

Data structure involved in function calls¶

We need to store calling function so that we can come back to it once answer of the called function has been evaluated.
Stack Data Structure is used to store function calls, their arguments, and return values.
In recursion, stack is called "call stack" and is used by the program to keep track of function calls in progress.

Problem 1 : Factorial of N¶

Given a positive integer N, find the factorial of N.

Question¶

If N = 5, find the factorial of N.

Choices

100
120
150
125

Solution

Assumptions: Create a function which -

takes an integer value N as parameter.
calculates and returns N!.
return type should be integer.

Main logic:

The factorial of N is equal to N times the factorial of (N-1)
We made assumption that sum(N) calculates and return factorial of N natural number. Similarly, sum(N-1) shall calculate and return the factorial of N-1 natural number. factorial(N) = N * factorial(N-1)

Base case: The base case is when N equals 0, i.e., 0! = 1

For example,

When we perform, factorial(N) = N * factorial(N-1), value of N keeps on decreasing by 1.
N -> (N-1) -> (N-2) ........ 2 -> 1
for N = 1 as well as 0, the factorial is 1.
So, we can write base case for N = 0 which will also cover for N = 1.

Pseudocode¶

int factorial(int N) {
    // base case
    if (N == 0) {
        return 1;
    }
    // recursive case
    return N * factorial(N - 1);
}

Dry Run¶

Problem 2 : Nth number in the Fibonacci Series¶

The Fibonacci sequence is a series of numbers in which each number is the sum of the two preceding numbers.

The sequence goes like this:

N	0	1	2	3	4	5	....
Fibonacci(N)	0	1	1	2	3	5	....

Given a positive integer N, write a function to compute the Nth number in the Fibonacci sequence using recursion.

Example

Input = 6
Output = 8

Explanation:

N	0	1	2	3	4	5	6
Fibonacci(N)	0	1	1	2	3	5	8

Fibonacci(6) = Fibonacci(5) + Fibonacci(4) = 3 + 5 = 8.

Question¶

If N = 7, find the Nth number in the fibonacci sequence.

Choices

8
5
13
10

Warning

Please take some time to think about the solution approach on your own before reading further.....

Nth number in the Fibonacci sequence Solution¶

Solution¶

Assumptions: Create a function which -

takes an integer value N as parameter.
calculates and returns Nth number in the fibonacci sequence.
return type should be integer.

Main logic: Recursively compute the (N-1)th and (N-2)th numbers in the sequence and add them together to get the nth number. fibonacci(N) = fibonacci(N - 1) + fibonacci(N - 2)

Base case: If N is 0 or 1, return the corresponding value in the Fibonacci sequence.

Since, according to the definition of fibonacci sequence, the smallest two possible values of N are N = 1 & N = 2, therefore, stop recursion as soon as N becomes 0 or 1.

Pseudocode¶

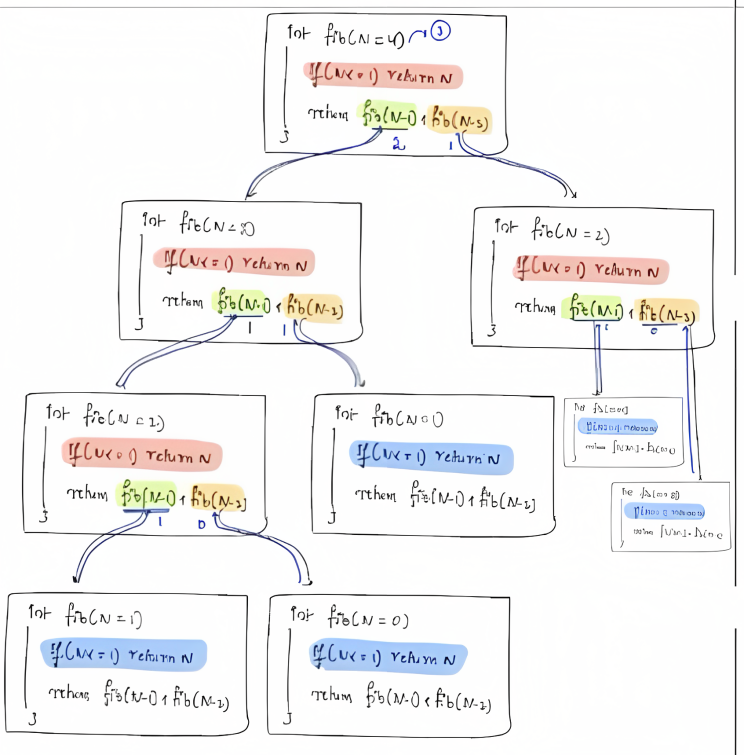
int fibonacci(int N) {
    // base case
    if (N == 0 || N == 1) {
        return N;
    }

    // recursive case
    return fibonacci(N - 1) + fibonacci(N - 2);
}

Function Call Tracing¶

Time Complexity of Recursion - using Recurrence Relation¶

Factorial(N)

Pseudocode¶

int factorial(int N) {
    // base case
    if (N == 0) {
        return 1;
    }
    // recursive case
    return N * factorial(N - 1);
}

Let's assume that time taken to calculate factorial(n) = T(n).
factorial(n) depends on the time taken by factorial(n-1) and other than that, constant work is being performed.
Time taken by factorial(n-1) = T(n-1) + O(1).
Therefore, for the sum of digits, the recursive relation will be defined as follows:

Equation 1¶

T(n) = T(n-1) + 1

1 is added because other than function calls, a constant amount of work is being done.

Substituting the value of T(n-1) = T(n-2) + 1

Equation 2¶

T(n) = T(n-2) + 2

Substituting the value of T(n-2) = T(n-3) + 1

Equation 3¶

T(n) = T(n-3) + 3

Substituting the value of T(n-3) = T(n-4) + 1

Equation 4¶

T(n) = T(n-4) + 4

After say k iterations, we shall reach to the base step.
The equation will be:

Equation 5¶

T(n) = T(n-k) + k

The base case shall take constant time:

T(0) = O(1)

We shall substitute the value of n - k = 0

=> n - k = 0 
=> n = k

Put the above value in a generalized equation, we get

T(n) = T(0) + n
T(n) = 1 + n
T(n) = O(n)

Hence we can say that.

T(n) = O(n)

Time Complexity of Fibonacci¶

Pseudocode¶

Function fibonacci(int n) {
    if (n == 0 || n == 1) return n;
    return fibonacci(n - 1) + fibonacci(n - 2);
}

Recurrence Relation is:

    T(n) = T(n-1) + T(n-2)

For easy calculation, we can write the recurrence relation as follows:

    T(n) = 2 * T(n-1)

It will evaluate to O(2^N)

Note to Instructor: Please evaluate above recurrence relation in class.

Another definition of Time Complexity¶

Time Complexity can also be defined as

Time taken in a single function call * Number of function calls

Question¶

How many recursive calls in the factorial(6)?

Choose the correct answer

Choices

0
2
6
10

Space Complexity of Recursive Code¶

The space complexity of recursion refers to the amount of memory required by a recursive algorithm as it executes. It is determined by the maximum amount of memory needed on the call stack at any given point during the recursion.

Space Complexity of factorial(N)¶

Total N call will be stored in the stack.

factorial(1)
factorial(2)
---------------
---------------
---------------
factorial(N-1)
factorial(N)

Maximum stack space used is N, hence space is O(N)

Hence, total O(N) space is required to execute all the recursive calls.

Space complexity of fibonacci(n)¶

If the time complexity of our recursive Fibonacci is O(2^n), what’s the space complexity?

Tempted to say the same?

NOTE to Instructor: Show it using a stack

SPACE COMPLEXITY can also be calculated using RECURSIVE TREE

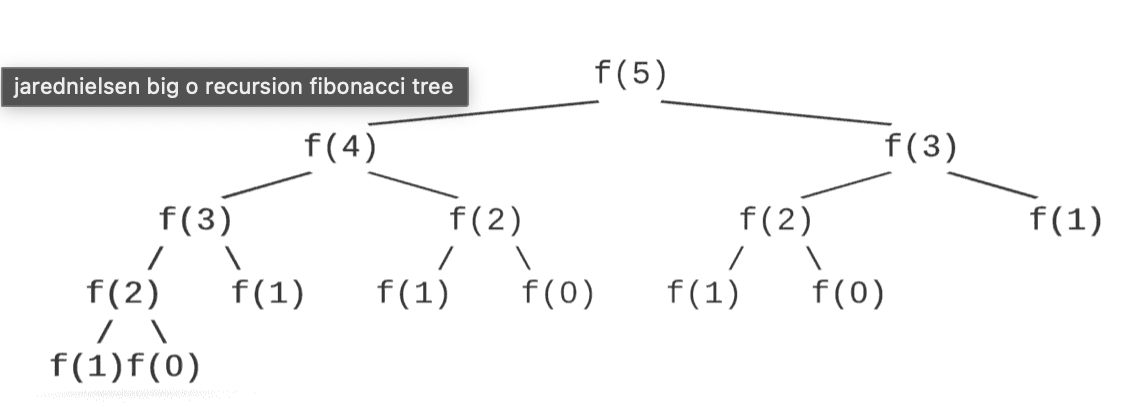
Please Note: This tree is known as Recursive Tree.

Space complexity is the amount of memory used by the algorithm.

When a function is called, it is added to the stack.

When a function returns, it is popped off the stack.

We’re not adding all of the function calls to the stack at once.

We only make n calls at any given time as we move up and down branches.

We proceed branch by branch, making our function calls until our base case is met, then we return and make our calls down to the next branch.

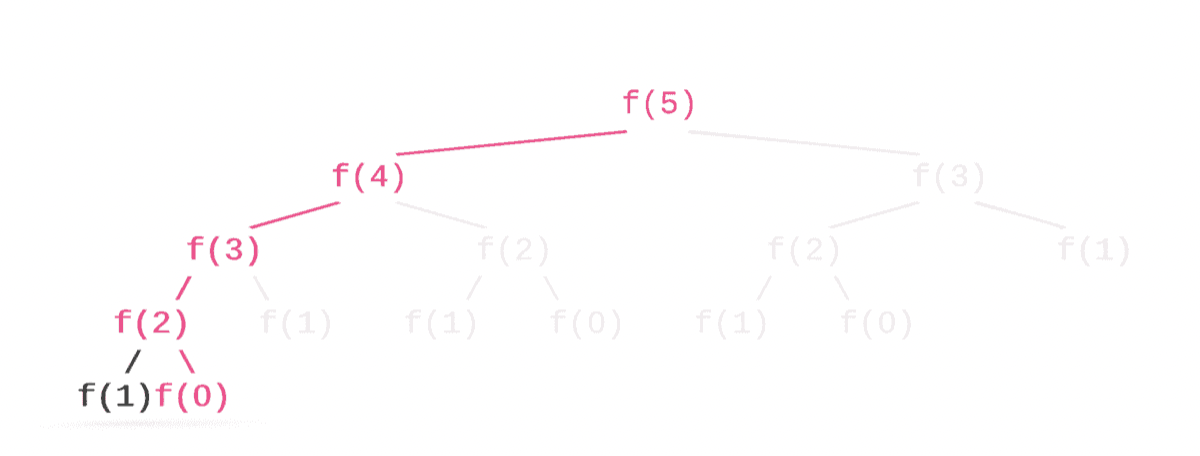
We can also define Space Complexity as height of the Recursive Tree.

Question¶

What is the height of tree for fibonacci(6) ?

Choose the correct answer

Choices

0
7
6
8