Searching 3: Binary Search on Answer

---

Problem 1 Painter's Partition

We have to paint all N boards of length [C0, C1, C2, C3 … CN - 1]. There are K painters available and each of them takes 1 units of time to paint 1 unit of the board.

Calculate and return the minimum time required to get the job done.

NOTE:

1. Two painters cannot share a board to paint. That is to say, a board cannot be painted partially by one painter, and partially by another.

2. A painter will only paint contiguous boards. This means a painter paints a continous subarray of boards

Example 1

Below are some of the possible configurations:

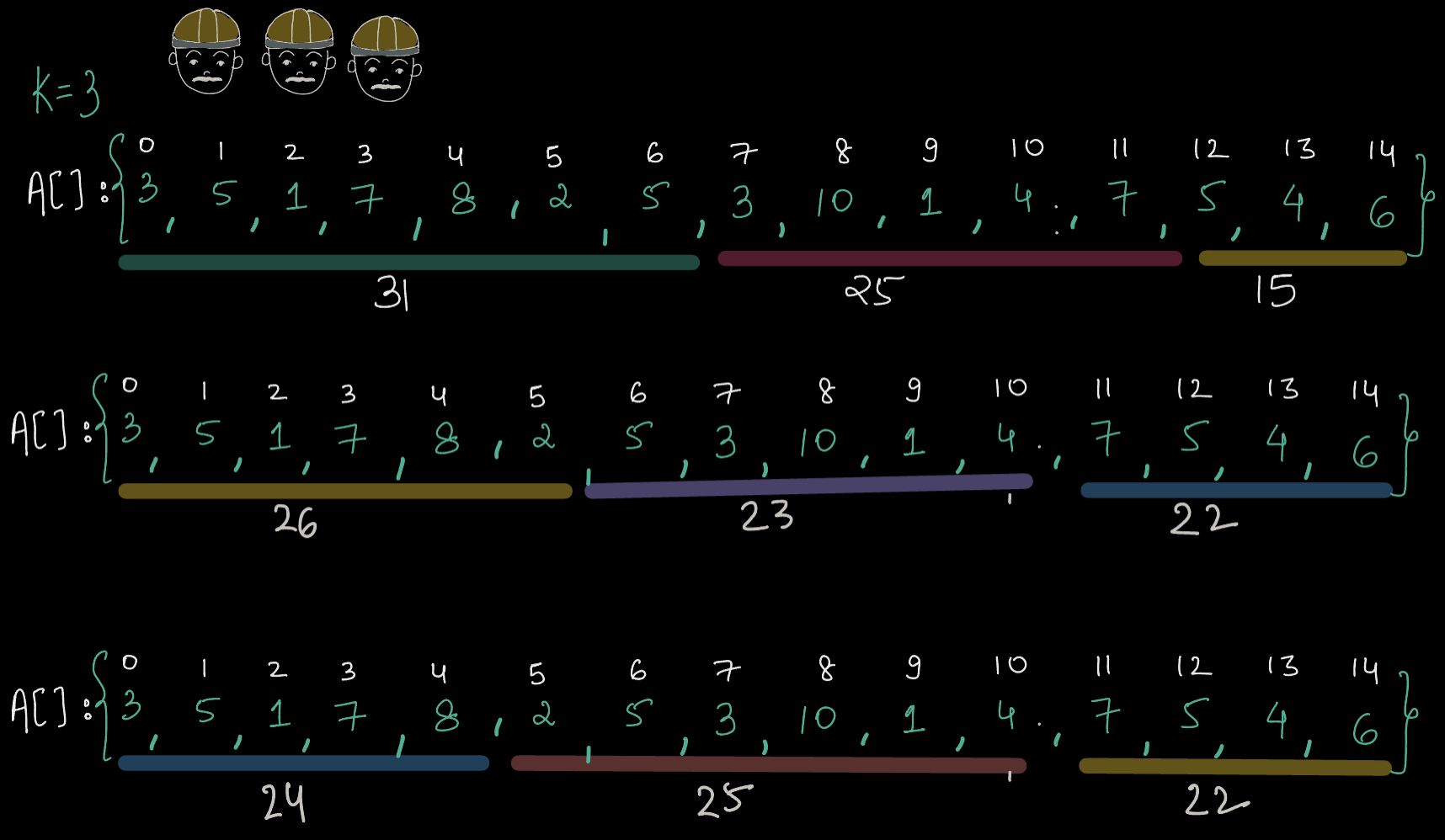
Configuration 1: Max is 31
Configuration 2: Max is 26
Configuration 3: Max is 25

Out of above least is 25, hence configuration 3 is better. We want to minimize the maximum value.

There can be more configurations, but you'll find the 3^rd to be the best, hence 25 is the answer.

Example 2

A = [10,20,30,40]
K = 2

P1 => red
P2 => green

Max = 70

Max = 60

Output

60

---

Warning

Please take some time to think about the solution approach on your own before reading further.....

Painter's Partition Greedy Approach

• Greedy Approach:- We can just divide the total time by total number of painters.
• One might think it as by dividing the boards among the painters would result in least time per painter
• But is this idea valid ?

Flaw:

A = [1,2,3,4,100] K = 2

According to Idea 1 :- \(110/2 = 55\)

But we see that it is impossible, because we can't divide the boards among two painters with 55 length each.

---

Question

What is the minimum time to get the job done?

A = [1,2,3,4,100] K = 2

Choices

• 55
• 100
• 1
• 110

Explanation:

The minimum time required to Finish the job is 100.

The configuration of the boards is as follows

• painter1 = [1, 2, 3, 4] = 10
• painter2 = [100] = 100

Thus the maximum of (10, 100) is the minimum time taken to complete the job.

Among all possible configuration 100 is the minimum time achieved.

---

Painter's Partition Binary Search

Lets's look at example below :-

[3, 5, 1, 7, 8, 2, 5, 3, 10, 1, 4, 7, 5, 4, 6] ans K = 4

Color code for each painter:

P1 -> Red
P2 -> Green
P3 -> Blue
P4 -> Orange

---

Search Space

Best Case

Say we have as many painters as the number of boards, in which case each painter can paint one board. The maximum value will be the answer.

Example:

A[ ] = {2, 5, 3, 8}, K = 4
Then 8 is the answer.

Worst Case

There is ony 1 painter. In this case, sum(array) is the answer.

So, our Search Space will be within range: [max(array) to sum(array)]

---

Target

The max time to complete the task

---

Condition

• Say we land at mid. How can we decide whether mid is the answer?
• We can check if we can complete the task within mid amount of time at max.
  • If yes, then we should save it as the answer and move left to try for a lesser time.
  • Else, move right(it means we will need more time to complete the task )

---

Painter's Partition Dry Run and Pseudocode

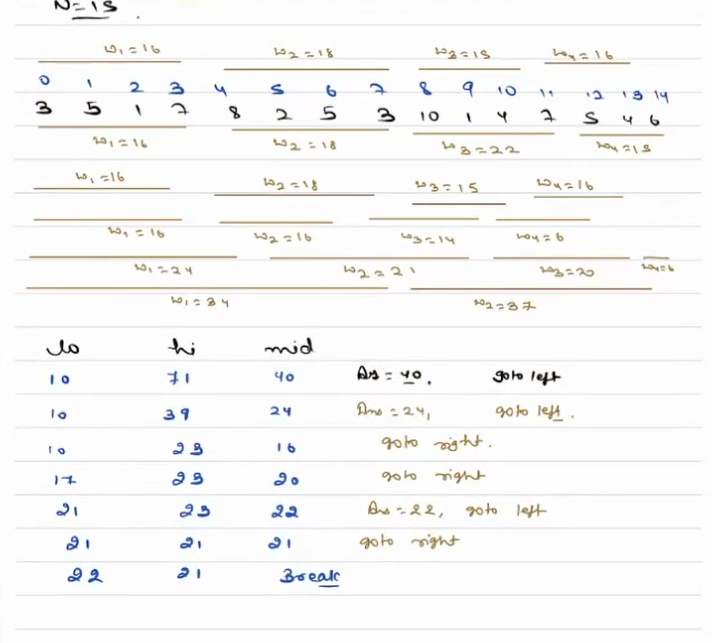
[3, 5, 1, 7, 8, 2, 5, 3, 10, 1, 4, 7, 5, 4, 6] ans K = 4

• Intially the Lo = 10 and Hi = 71 (By using above defined criteria for search space) therefore using the above algorithm Mid = \(10 + (71 - 10)/2 = 40\) then we check if it is possible to paint all boards in atleast 40 units below is the configuration that satisfy the condition :-

  • Painter P1 takes = \(3 + 5 + 1 + 7 + 8 + 2 + 5 + 3 = 34\)
  • Painter P2 takes = \(10 + 1 + 4 + 7 + 5 + 4 + 6 = 37\)
  • 
  • Since the condition is satisfied let's go to left i.e. \(Hi = mid -1 = 40 - 1 = 39\)

• Now Hi = 39 and Lo = 10; Mid = \(10 + (39 - 10)/2 = 24\)

  • Painter P1 takes = \(3 + 5 + 1 + 7 + 8 = 24\)
  • Painter P2 takes = \(2 + 5 + 3 + 10 + 1 = 21\)
  • Painter P3 takes = \(4 + 7 + 5 + 4 = 20\)
  • Painter P4 takes = 6
  • 
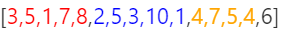
  • Since the condition is satisfied let's go to left i.e. \(Hi = mid -1 = 24 - 1 = 23\)

• Now Hi = 23 and Lo = 10 therefore using the above algorithm Mid = \(10 + (23 - 10)/2 = 16\) then we check if it is possible to paint all boards in atleast 10 units We find that there is no configuration that satisfy the condition therefore we go to right.

• Similarly we follow the algorithm to arrive at the solution.

Pseudocode

// Find minimum painters required for given maximum length (Length that painter can paint)
paintersNumber(arr[], N, mid, K) {
  res = 0, numPainters = 1;

  for (i = 0; i < N; i++) {
    res += arr[i];

    if (res > mid) {
      res = arr[i];
      numPainters++;
    }
  }
  //if we have used less than or equal to given number of painters,
  //then the configurations works
  if (numPainters <= K) return true;
  else return false;
}

partition(arr[], N, K) {
  Lo = maxEle(arr, N);
  Hi = sumArr(arr, N);

  while (Lo <= Hi) {
    mid = Lo + (Hi - Lo) / 2;

    if (paintersNumber(arr, N, mid, K))
      ans = mid
    Hi = mid - 1;
    else
      Lo = mid + 1;
  }
  return ans;
}

Complexities

Time Complexity: O(log (sum - max) * N )
Space Complexity: O(1)

---

Question

What is the time complexity of the Painters Partition Problem?

Choices

• O( log(k) * (sum(boards) - max(boards)))
• O(k * log(sum(boards) - max(boards)))
• O(N * log(sum(boards) - max(boards)))
• O(k * log N)

---

Problem 2 Aggresive Cows

Given N cows & M stalls ,all M stalls are located at the different locations at x-axis, place all the cows such that minimum distance between any two cows is maximized.

Note :

1. There can be only one cow in a stall at a time
2. We need to place all cows

Testcase 1

stalls = [1, 2, 4, 8, 9]
cows = 3
stall = 5

Solution

T = 3

Explaination TestCase 1

1	2	4	8	9	Min distance
c1	c2	c3			1
c1		c2		c3	3
c1			c2	c3	1

• If we put cows according to the first configuration then min distance = 1 because of c1 and c2 (shortest distance between any two cows is 1).
• If we put cows according to the Second configuration then min distance = 3 because of c1 and c2 (shortest distance between any two cows is 3)
• If we put cows according to the third configuration then min distance = 1 because of c2 and c3 (shortest distance between any two cows is 1).
• Therefore answer = max(1,3,1) = 3

Testcase 2

stalls  = [2, 6, 11, 14, 19, 25, 30, 39, 43]
cows = 4
stall = 9

Solution

T = 12

Explaination TestCase 2

2	6	11	14	19	25	30	39	43	Min distance
c1	c2	c3	c4						3
c1		c2		c3		c4			8
c1			c2			c3		c4	12

• If we put cows according to the first configuration then min distance = 3
• If we put cows according to the Second configuration then min distance = 8
• If we put cows according to the third configuration then min distance = 12
• Therefore answer = max(3,8,12) = 12

---

Question

What is the objective of the problem described?

Choices

• Place cows in stalls randomly.
• Place cows in stalls such that the distance between any two cows is minimized.
• Place cows in stalls such that the minimum distance between any two cows is maximized.
• Place cows in stalls such that the total distance is minimized.

---

Question

What will be the maximum value of the distance between the closest cows in this case? A: 0, 3, 4, 7, 9, 10 K = 4

Choices

• 10
• 4
• 3
• 2

Explanation:

The 4 cows are placed in stalls at 0, 3, 7, 10. This is the optimal configuration.

The value between the closest cows can be found by
= min(3 - 0, 7 - 3, 10 - 7)
= min(3, 4, 3)
= 3

Thus the maximum result is 3 over all possible configurations.

---

Warning

Please take some time to think about the solution approach on your own before reading further.....

Aggresive Cows Binary Search Approach

Let's use testcase 2 to get the intuition of the question.

This question is similar to Painter's Partition problem. Instead of minimising the maximum answer, we have to maximise the minimum distance.

Search Space

• Worst Case:

If say there are same cows as the number of stalls, then we place each cow at 1 stall. Then we can find difference between adjacent stalls. The minimum out of them is the answer.

Example:

A[ ] = {4, 7, 14, 20}
7 - 4 = 3
14 - 7 = 7
20 - 14 = 6
min(3, 7, 6) = 3(answer)
Though, we can take 1 as the minimum value.

• Best Case:

There are two cows. Then, we can place them at the corner stalls. The distance between first and last stall will be the answer.

Search Space: [1 A[N-1]-A[0]]

Condition

Say we land at mid, now we can check if it is possible to keep cows at a minimum distance of mid.

• If yes, save it and check for farther distance, i.e, move right.
• Else, if keeping at a distance of mid is not possible, then we should try reducing the distance; hence, move left.

Example 1:

Let's check if we can put 4 cows at minimum distance of 20.

2	6	11	14	19	25	30	39	43	Min distance
c1					c2				20

In above configuration minimum distance is 20 but we are unable to accommodate all cows(no place for c3 and c4). This means that we have to reduce the distance to accomodate all cows.

Example 2:

Let's check if we can put cows at minimum distance of atleast 5 below is a configuration that satisfy the condition.

2	6	11	14	19	25	30	39	43	Min distance
c1		c2		c3	c4				5

Since we are able to place all cows at a minimum distance of 5, we should save it as answer and try to maximise this distance.

---

Aggresive Cows Dry Run and Pseudocode

Below is the trace of algorithm on above Example :-

• Intially the Hi = 41 and Lo = 3 (By using above defined criteria for search space) therefore using the above algorithm Mid = \(3 + (41 - 3)/2 = 22\) then we check if it is possible to accommodate 4 cows completely in the shelters with min distance being 22 units We could not find any such configuration that satisfy the condition (got to left) below one failed configuration :-

2	6	11	14	19	25	30	39	43	Min distance
c1			c2				c3		N/A since all cows not accommodated

• Now the Hi = 21 and Lo = 3 therefore using the above algorithm Mid = \(3 + (21 - 3)/2 = 12\) then we check if it is possible to accommodate 4 cows completely in the shelters with min distance being 12 units below is configuration that satisfies the condition (we go to right) :-

2	6	11	14	19	25	30	39	43	Min distance
c1			c2			c3		c4	12

• Now the Hi = 21 and Lo = 13 therefore using the above algorithm Mid = \(13 + (21 - 13)/2 = 17\) then we check if it is possible to accommodate 4 cows completely in the shelters with min distance being 17 units We could not find any such configuration that satisfy the condition (got to left) below one failed configuration :-

2	6	11	14	19	25	30	39	43	Min distance
c1				c2			c3		N/A since all cows not accommodated

Pseudocode

bool check(v[], int x, int c) {
  n = v.size();
  count = 1;
  last = 0;
  for (i = 0; i < n; i++) {
    if (v[i] - v[last] >= x) {
      last = i; //cow placed
      count++;
    }
    if (count >= c) {
      return true;
    }
  }
  return false;
}

// Function to find the maximum possible
// minimum distance between the cows
aggressive_cows(v[], size, cows) {
  int lo = 0;
  for (i = 1; i < n; i++) {
    lo = min(lo, v[i] - v[i - 1]);
  }
  hi = v[n - 1] - v[0];
  ans = -1;

  // Applying Binary search
  while (lo <= hi) {
    mid = lo + (hi - lo) / 2;
    if (check(v, mid, cows)) {
      ans = mid;
      lo = mid + 1;
    } else {
      hi = mid - 1;
    }
  }

  return ans;
}

---

Binary Search Problems Identification

• These type of problems generally has following characteristics :-
• There are two or three parameter & constraints
• Requirement is to maximize or minimize the given parameter
• One tricky point is to find search space which is generally the parameter asked to maximize or minimize.
• The problem should be Monotonic in nature i.e after one point it is not feasible to solve or vice versa.

---