Searching 1: Binary Search on Array¶

Introduction to Searching - Story¶

Let us say you lost something
When you go to the police, you tell them what to search for—the target—and where to search—the search space.
It is easy to look for a word in the dictionary as compared to searching for a word in a book or newspaper. This is because along with the target element, we also have defined search space(alphabetical order).
In the Phone book as well, we have names sorted in the contacts list, so it's easier to find a person's number.
Search space - The area where we know the result exists and we search there only
Target - The item we are looking for
Condition - Some condition to discard some part of the search space repeatedly to make it smaller and finally reach the result.
Binary Search - divide the search space into two parts and repeatedly keep on neglecting one-half of the search space.

Question¶

In binary search, at each step, the search range is typically:

Choices

Halved
Tripled
Doubled
Reduced by one

Binary Search¶

Binary Search Question¶

Given a sorted array with distinct elements, search the index of an element k, if k is not present return -1.

arr[] =

3	6	9	12	14	19	20	23	25	27

Brute Force Approach - Linear Search¶

We can traverse the array and compare each element with the target element. This is done until we find the target element or all the elements of the array are compared. This method is called linear search and the time complexity in the worst case is O(N) where N is the number of elements in the array.
We can perform the same operation with less number of comparisons and with better time complexity using Binary Search as the array is sorted.

Binary Search Approach¶

Binary search has three elements,
- Search space - array
- target - we are given a target element to be found from the array
- condition ->
- array is sorted, say I am at some random position, if I compare the current element with the target element.
- If current_element > target_element, I can discard all the element appearing before current element and the target_element as they will always be smaller than current element.
- Similarly, if the current_element < target_element, the target element and the elements appearing after it can be discareded.
- We have all the three elements and thus, binary search can be easily applied to it.
Let us take the middle index.
if arr[mid] == k, i.e. we found the target, we return the index of the target.
if arr[mid] < k i.e. the target exists on the right side of the array so the left half is of no use and we can move to the right.
Similarly, if arr[mid] > k i.e. the target exists on the left, and the right half can be discarded.

Dry Run¶

Let us dry run binary search for the array:

0	1	2	3	4	5	6	7	8	9
3	6	9	12	14	19	20	23	25	27

First Iteration:

low = 0, high = 9
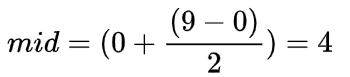
arr[4] (14) > target (12) (Since 14 already is larger and array is sorted, so all the elements to the right of mid will be even larger, hence, we should move left.)
go left -> high = mid - 1 = 3

Second Iteration:

low = 0, high = 3
the mid =
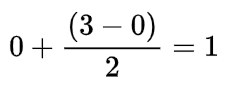
arr[1] (6) < target (12)
go right -> left = mid + 1 = 2

Third Iteration:

low = 2, high = 3
the mid =
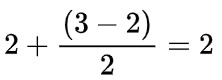
arr[2] (9) < target (12)
go right -> left = mid + 1 = 3

Fourth Iteration:

low = high = 3 = mid
arr[3] (12) == target (12)
break;

Dry run for target element not present, let's say 11.

Binary Search Pseudo Code¶

int search(int arr[], int N, int k) {
  lo = 0, hi = N - 1;
  while (lo <= hi) {
    mid = lo + (hi + lo) / 2;
    if (arr[mid] == k) {
      return mid;
    } else if (arr[mid] < k) {
      lo = mid + 1;
    } else {
      hi = mid - 1;
    }
  }
  return -1;
}

Complexity¶

Time Complexity: O(log N)
Space Complexity: O(1)

Question¶

If the element 'k' is found in a sorted array, what will be the time complexity of binary search?

Choices

O(1)
O(log n)
O(n)
O(n²)

Best Practices - Binary Search¶

Some write the formula of mid calculation as 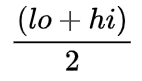but it is incorrect, as in some cases it may lead to overflow.
e.g, Let us assume that maximum number stored by a particular data type is 100 (It's Integer.Max_Int but just to make maths easy, assuming its 100), and the number of elements in the array is 100 for which last index will be 99 for zero indexing and thus, is in the limit.
There is the posibility that the target element is at the position 98 and value of low = 98 and high = 99. When we calculate mid for this scenario, the high and the low are in limits but while calculating the mid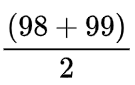 first the sum 197 will be calculated and stored. This will cause the overflow as the limit of the variable is 100 only(assumption).
This may result in incorrect or negative value.
Whereas, when we write 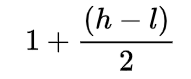we will get 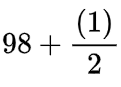which even in the worst case be 99 and will not overflow.

Identify 2024's First Email¶

All emails in your mailbox are sorted chronologically. Can you find the first mail that you received in 2024?

Binary Search Problems - Find first occurrence¶

Given a sorted array of N elements, find the first occurrence of the target element.

arr[] =

-5	-5	-3	0	0	1	1	5	5	5	5	5	5	5	8	10	10	15	15

For 5 first occurence is at index 7 so we have to return 7.

Brute force approach is linear search.
Now the array is sorted so using binary search we can find at least one of the occurences of the given target element.
The challenge is to find the first occurence. What we know about the first occurence is that it is always going to be the current position or in the left.
Now in left, we can do linear search but in worst it will take about O(N) time complexity.
What we have got is the potential answer, it can or cannot be final anser.
We can store the current position in a variable, in case it is the first occurence. Next, we can apply binary search in the left side of the array.
The only change we are required to make is to not stop if we find the target element instead keep looking in the left side of the array until low > high.
If the mid == target store mid, go left.
else if mid > target go right.
else go left.

Dry run for the example¶

0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
-5	-5	-3	0	0	1	1	5	5	5	5	5	5	5	8	10	10	15	15

First Iteration:

low = 0, high = 18
the mid =
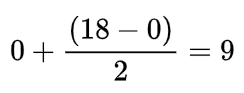
arr[9] (5) == target (5)
ans = 9
go left -> high = mid - 1 = 8

Second Iteration:

low = 0, high = 8
the mid =
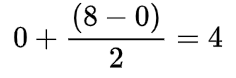
arr[4] (0) < target (5)
go right -> left = mid + 1 = 5

Third Iteration:

low = 5, high = 8
the mid =
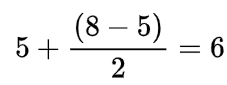
arr[6] (1) < target (5)
go right -> left = mid + 1 = 7

Fourth Iteration:

low = 7, high = 8
the mid =
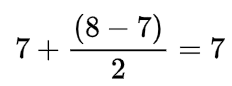
arr[7] (5) == target (5)
go left -> high = mid - 1 = 6
break;

Question¶

When searching for the first occurrence of an element in a sorted array, what should you do if the current element matches the target 'k'?

Choices

Return the current index
Continue searching in the right subarray
Continue searching in the left subarray
Stop searching immediately

Question¶

What is the time complexity of finding the first occurrence of an element in a sorted array using binary search?

Choices

O(log n)
O(n)
O(1)
O(n²)

Complexity¶

Time Complexity: O(logn) (Everytime you are discarding the search space by half).
Space Complexity: O(1)

Follow up question¶

Try for the last occurence

Find the unique element¶

Question

Every element occurs twice except for 1, find the unique element.
Note: Duplicate elements are adjacent to each other but the array is not sorted.

Example:

Warning

Please take some time to think about the solution approach on your own before reading further.....

Brute Force Approach¶

The brute force approach can be comparing A[i] with A[i+1]. If (A[i]!=A[i+1]), then A[i] is the unique element.

Optimal Approach¶

Can we apply Binary Search ?
- Say we land at mid, how to know current element is the answer? => We can check element at its right and at its left. If both are different, then mid is the ans.
- If A[mid] is not the answer, then how to decide in which direction shall we move?
  - For that, let's make some observation.
  - We are given that only one element is unique, there are two occurences of remaining elements.
  - Can you make some observation w.r.t first occurrences of elements before and after unique element ?
  - Before unique element, first occurrences are at even index. After unique element, all first appear at odd indices.

Let us say the array is as follows:

0	1	2	3	4	5	6	7	8	9	10
7	7	6	6	3	8	8	1	1	9	9

3 is unique.
First occurrence of 7 and 6 is at index even and after 3, first occurrences of elements, 8, 1, 9 is at odd index.

Steps for applying Binary Search¶

Land at mid, if A[mid] != A[mid-1] && A[mid] != A[mid+1], then A[mid] is the answer.
NOTE: To avoid accessing invalid indices, above conditions shall be modified as follows-
- mid == 0 || A[mid] != A[mid-1]
- mid == N-1 || A[mid] != A[mid+1]
Else, we will check index of first occurrence of the element we landed on.
- If index is even, then unique element must be present on right.
- Else, on left.

Dry Run for An Example¶

Index	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14
Elements	3	3	1	1	8	8	10	10	19	6	6	2	2	4	4

For the above array,

1^st Iteration:

low = 0, high = 14,
\(mid = 0 + (14-0)/2 = 7\)
It's not unique.
arr[mid] == arr[mid - 1] -> mid - 1 is the first occurence.
mid - 1 = 6 which is even -> go to right
low = mid + 1

2^nd iteration:

low = 8, high = 14
\(mid = 8 + (14-8)/2 = 11\)
It's not unique.
mid - 1 = 10
arr[mid] != arr[mid - 1]
mid + 1 = 12
arr[mid] == arr[mid + 1] -> mid is the first occurence.
mid % 2 != 0 i.e. mid is odd and thus, left subarray has the unique element. We will move high to mid - 1 = 10.

3^rd iteration:

low = 8, high = 10
\(mid = 8 + (10-8)/2 = 9\)
Its not unique.
mid - 1 = 8
arr[mid] != arr[mid - 1]
mid + 1 = 10
arr[mid] == arr[mid + 1] -> mid is the first occurence.
mid % 2 != 0 i.e. mid is odd and thus, left subarray has the unique element. We will move high to mid - 1 = 8.

4^th iteration:

low = 8, high = 8
mid = (8 + (8 - 8) / 2) = 8
mid - 1 = 7
arr[mid] != arr[mid - 1]
mid + 1 = 9
arr[mid] != arr[mid + 1] -> mid is the unique element. We will terminate the loop.

Pseudo Code¶

int findUnique(int arr[], int N) {

  lo = 0, hi = N - 1;

  // binary search
  while (lo <= hi) {
    mid = lo + (hi - lo) / 2;

    if ((mid == 0 || arr[mid] != arr[mid - 1]) && (mid == N - 1 || arr[mid] != arr[mid + 1])) { //checking mid is unique
      return A[mid];
    } else if (mid == 0 || arr[mid] == arr[mid - 1]) { //at first occurrence
      if (mid % 2 == 0) lo = mid + 2;
      else hi = mid - 1;
    } else { //at second occurrence
      if (mid % 2 == 0) hi = mid - 2;
      else lo = mid + 1;
    }
  }
}

Complexities¶

Time Complexity: O(log(N)
Space Complexity: O(1)

Increasing Decreasing Array¶

Given an increasing decreasing array with distinct elements. Find max element.

Examples

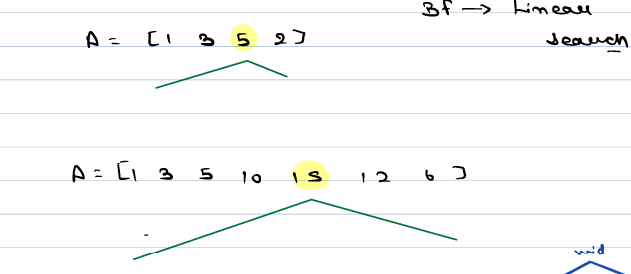
arr[] = {1, 3, 5, 2}
In the above array 5 is the max value.
arr[] = {1, 3, 5, 10, 15, 12, 6}
In the given example max element is 15

The increasing decreasing array will look something like this:

Warning

Please take some time to think about the solution approach on your own before reading further.....

Solution¶

Increasing decreasing arrays are the array that increases first and after reaching its peek it starts decreasing. We are supposed to find the peek or the max element of the array. The increasing side is sorted in ascending order and the decreasing side is sorted in descending order.
Brute force approach is a linear search with O(N) time complexity.
But as we see the elements are sorted in increasing and then decreasing order, so can we do better than O(N) time complexity?
Can we apply Binary Search? What do we need ?
- Search space -> array
- target -> peak element
- Condition: ->
- Case 1: if(arr[mid] > arr[mid - 1] && arr[mid] < arr[mid + 1]) return mid;
  - If immediate left and right are less than current element than we are at peek element.
- Case 2: if(arr[mid] > arr[mid - 1] and arr[mid] < arr[mid + 1]) go right;
  - Implies our mid is at the part of the array where it is still increasing. So the peek will be at the right side of the array.
- Case 3: go left
- This infers that mid is at the decreasing side of the array and peek must be at left.

Pseudocode¶

Local Minima in an Array¶

Given an array of N distinct elements, find any local minima in the array

Local Minima - a no. which is smaller than its adjacent neighbors.

Examples

A = {3,6,1,0,9,15,8}
- Here, we have 3 local minima, 3, 0, and 8.
- 3 < 6, 0 < 1 && 0 < 9, and 8 < 15. All these are smaller than their left and right neighbours.
B = {21,20,19,17,15,9,7}
- All the numbers are in decreasing order, so we only have one local minima 7.
C = {5,9,15,16,20,21}
- Similarly, all the numbers are strictly increasing so 5 is the only local minima in this example.
D = {5,8,12,3}
- Here, the series first increases and then decreases. So we have two local minima 5 and 3. 5 < 8 and 3 < 12.
This can have multiple local minima
We have to return any local minima

Solution¶

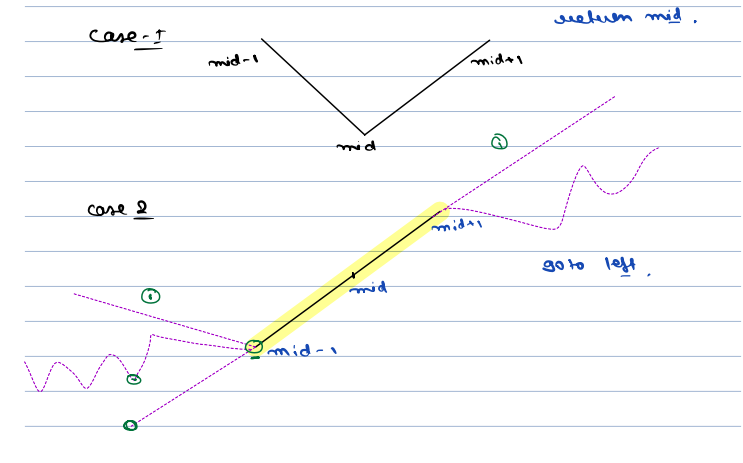
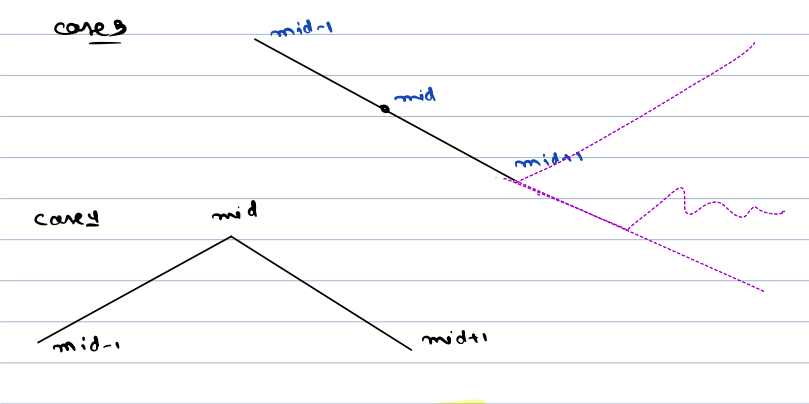
Case 1: Current element is smaller than the next and the previous element returns the current element, since this is local minima.
Case 2: If the current element is greater than the previous element and less than the next element.

Here we are not looking for global minimia, we are looking for local minima. If arr[mid - 1] < arr[mid] < arr[m + 1] there are two posiblities, either arr[m - 1] is one of the local minima or we will definitely find a local minima in left direction as elements to the left are in decreasing order.
Case 3: If the current element is greater than the next element and is smaller than the previous element go to the right. As Left may or may not have local minima but the right will definitely have local minima.
Case 4: The current element is greater than the previous as well next element. Then we can go to either the left or to the right, because both will contain atleast one local minima.

Pseudo Code¶

int localMinima(int[] A) {
  l = 0, h = n - 1;
  while (l <= h) {
    mid = l + (h - l) / 2;
    if ((mid == 0 || arr[mid] < arr[mid - 1]) && (mid == N - 1 || arr[mid] < arr[mid + 1])) {
      return mid;
    } else if (mid == 0 || arr[mid] < arr[mid - 1]) {
      l = mid + 1;
    } else {
      h = mid - 1;
    }
  }
}

Dry run¶

Index	0	1	2	3	4	5	6	7
Element	9	8	2	7	6	4	1	5

1^st Iteration

low = 0, high = 7
mid = 3
The element to the left of mid -> 2 < 7 Thus, 7 cannot be local minima.
The array is increasing and thus, one of the local minima must be in the left of the array, so we will change high = mid - 1 = 2.

2^nd iteration

low = 0, high = 2
mid = 1
Element to the left of mid -> 9 > 8
Element to the right of mid -> 2 < 8
8 cannot be local minima. As 2 is smaller than 8, we are at decreasing array and thus, the local minima must exist in the right.
low = mid + 1

3^rd iteration

low = 2, high = 2
mid = 2
Element to the left of mid -> 2 < 8
Element to the right of mid -> 2 < 7
2 is our local minima.

Complexities¶

Time Complexity: O(log(N))
Space Complexity: O(1)