Sorting 2: Quick Sort & Comparator Problems¶

Problem 1 Partition the array¶

Problem Description

Given an integer array, consider first element as pivot, rearrange the elements such that for all i:

if A[i] < p then it should be present on left side
if A[i] > p then it should be present on right side

Note: All elements are distinct

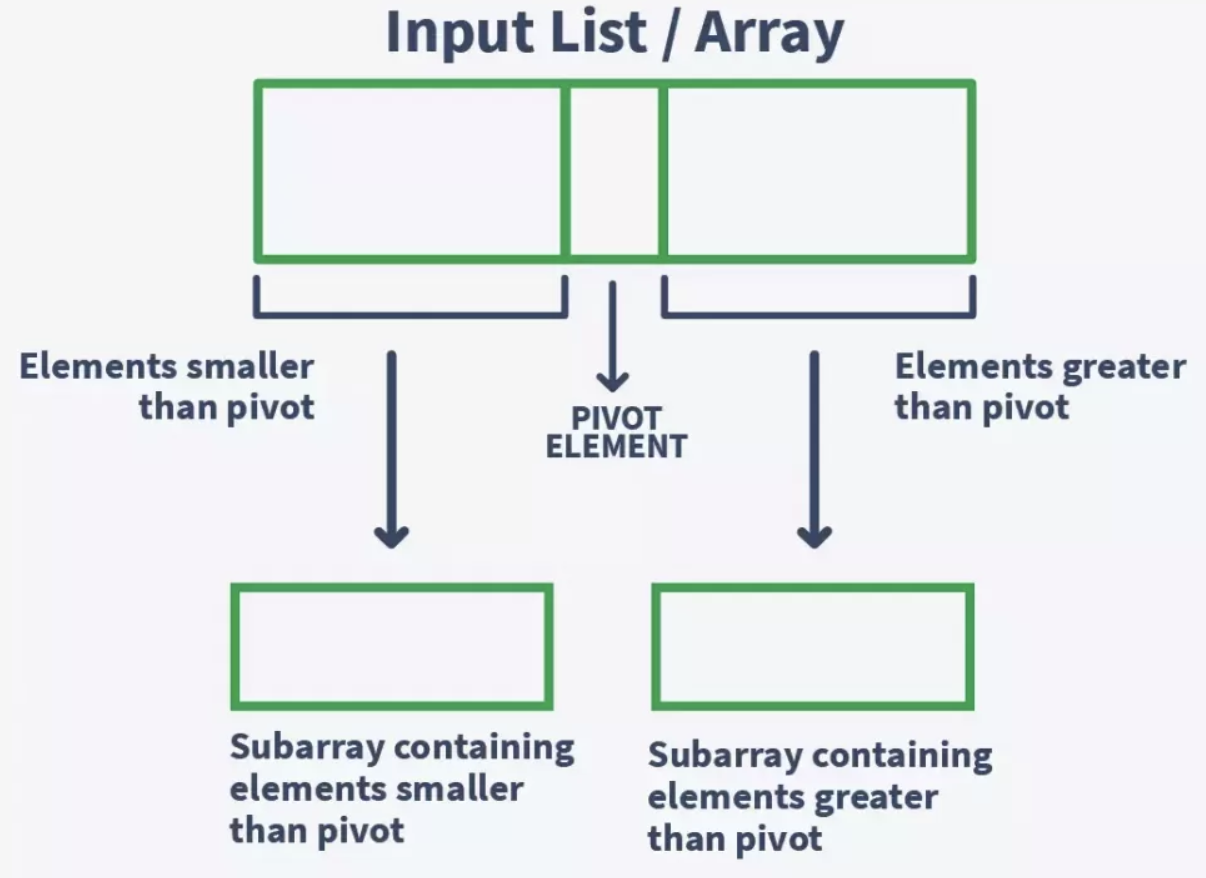
Example:¶

The State of the array after Partitioning will be:

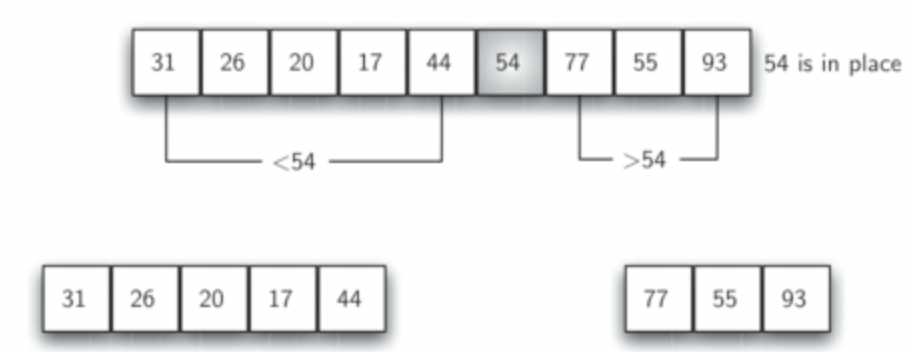
Question¶

Given an integer array, consider first element as pivot p, rearrange the elements such that for all i:

if A[i] < p then it should be present on left side
if A[i] > p then it should be present on right side

A = [10, 13, 7, 8, 25, 20, 23, 5]

Choices

left side = [10, 7, 5, 8] right side = [10, 13, 25, 20, 23]
left side = [10, 13, 7, 8] right side = [25, 20, 23, 5]
left side = [13, 25, 20, 23] right side = [7, 8, 5]
left side = [7, 8, 5] right side = [13, 25, 20, 23]

Explanation:

The pivot value is 10

The elements lesser than the pivot are [7, 8, 5]
The elements greater than the pivot are [13, 25, 20, 23]

Thus, left side = [7, 8, 5] right side = [13, 25, 20, 23]

Partition the array Approach¶

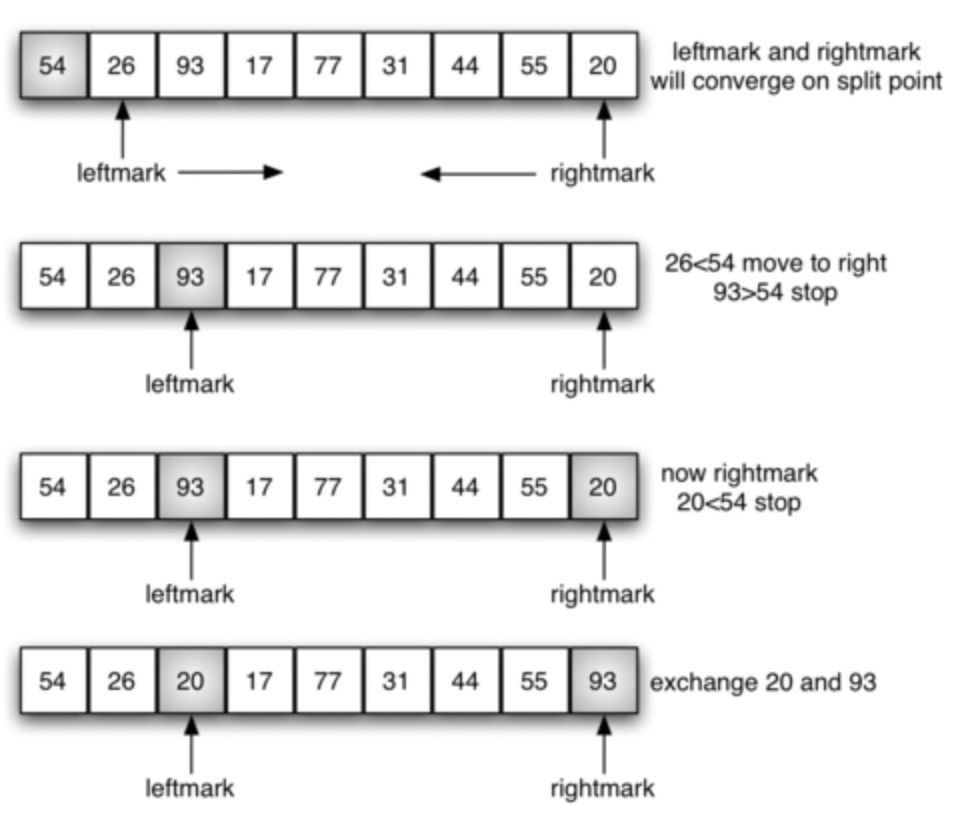
Partitioning begins by locating two position markers—let’s call them leftmark and rightmark—at the beginning and end of the remaining items in the list.
The goal of the partition process is to move items that are on the wrong side with respect to the pivot value while also converging on the split point.

Process¶

We begin by incrementing leftmark until we locate a value that is greater than the pivot value.
We then decrement rightmark until we find a value that is less than the pivot value.
At this point we have discovered two items that are out of place with respect to the eventual split point. For our example, this occurs at 93 and 20. Now we can exchange these two items and then repeat the process again.

Continue:

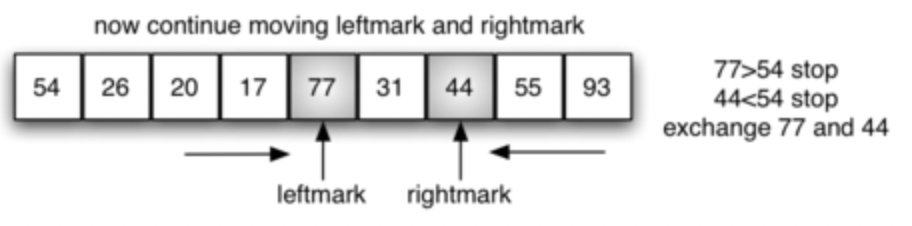
At the point where rightmark becomes less than leftmark, we stop. The position of rightmark is now the split point. The pivot value can be exchanged with the contents of the split point and the pivot value is now in place

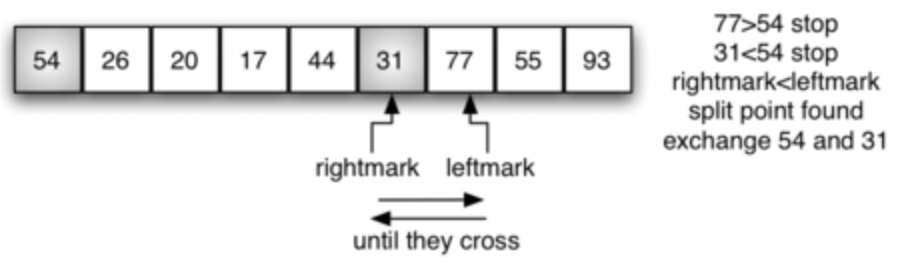
Now, we can exchange the 54(Pivot) with 31

Pseudocode¶

partition(A,first,last):
   pivotvalue = A[first]

   leftmark = first+1
   rightmark = last

   while leftmark <= rightmark:

       if A[leftmark] <= pivotvalue:
           leftmark = leftmark + 1

       else if A[rightmark] > pivotvalue:
           rightmark = rightmark -1

       else:
           temp = A[leftmark]
           A[leftmark] = A[rightmark]
           A[rightmark] = temp

    // swap pivot element with element present at rightmark
   temp = A[first]
   A[first] = A[rightmark]
   A[rightmark] = temp

Quick Sort¶

Sorting is the process of organizing elements in a structured manner.

Quicksort is one of the most popular sorting algorithms that uses nlogn comparisons to sort an array of n elements in a typical situation. Quicksort is based on the divide-and-conquer strategy. We’ll take a look at the Quicksort algorithm in this session and see how it works.

A quick sort first selects a value, which is called the pivot value.
Although there are many different ways to choose the pivot value, we will simply use the first item in the list.
The role of the pivot value is to assist with splitting the list.
The actual position where the pivot value belongs in the final sorted list, commonly called the split point, will be used to divide the list for subsequent calls to the quick sort.

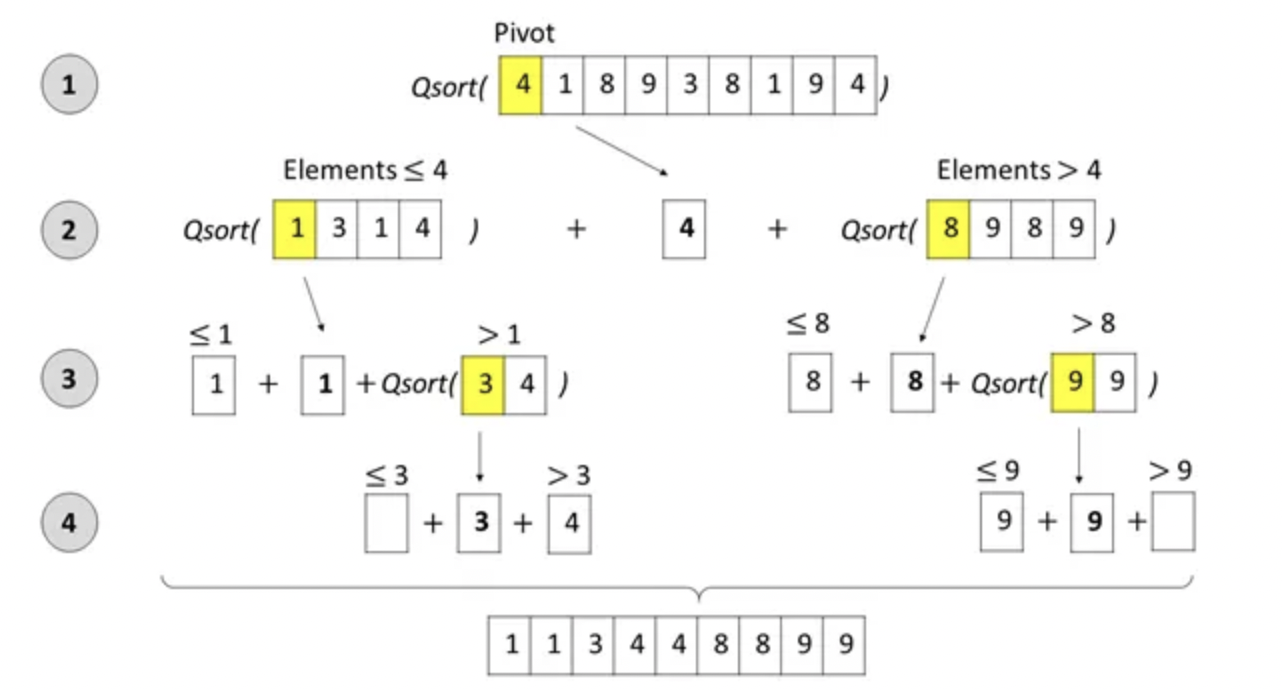
As per the previous example,

Now that there are two separate subarrays, we can apply partitioning on both separately and recursively. With each call, pivot element will be placed at its correct possition and eventually all elements will come at their correct place.

Steps to execute Quick Sort¶

Pick: Select an element.
Divide: Split the problem set, move smaller parts to the left of the pivot and larger items to the right.
Repeat and combine: Repeat the steps on smaller subarrays and combine the arrays that have previously been sorted.

Dry Run¶

Pseudocode¶

Below is the code for QuickSort

void quicksort(int[] A, int start, int end) {
  if (start < end) {
    int pivotIndex = partition(A, start, end);
    quicksort(A, start, pivotIndex - 1);
    quicksort(A, pivotIndex + 1, end);
  }
}

Quick Sort Time Complexity and Space Complexity¶

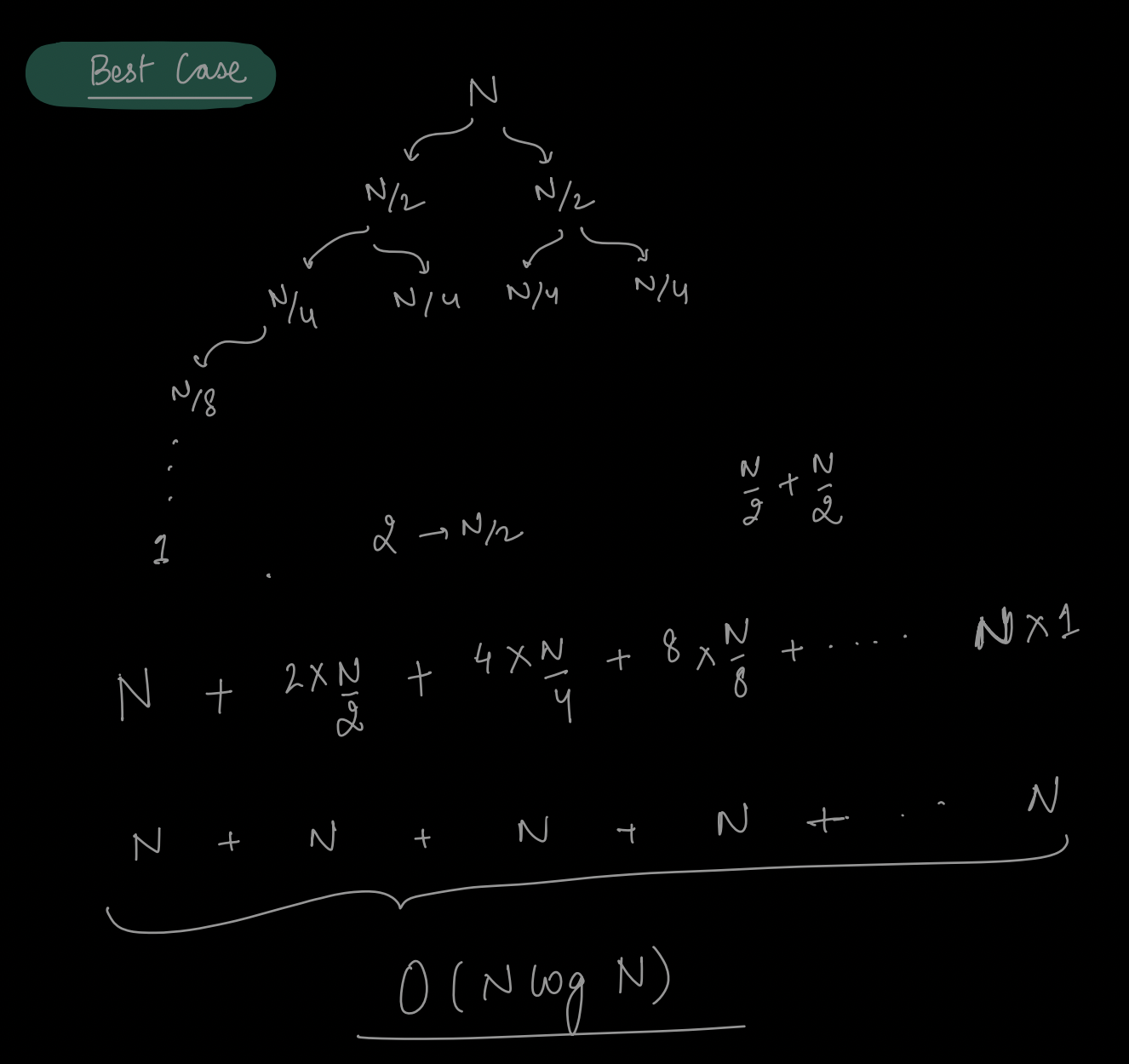
Best-Case Time Complexity:¶

The best-case scenario for QuickSort occurs when the pivot chosen at each step divides the input into approximately equal-sized subarrays.

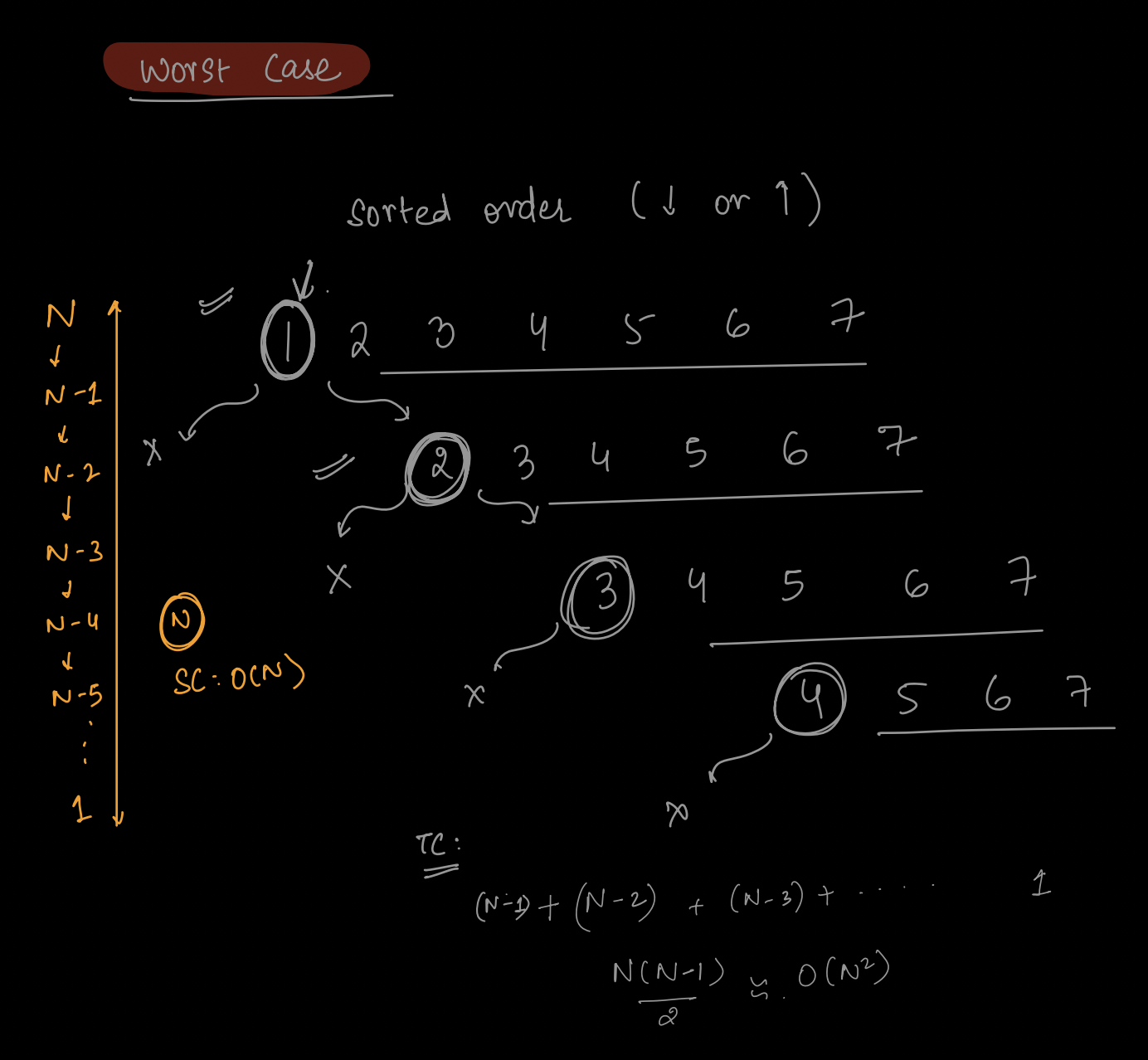
Worst-Case Time Complexity:¶

The worst-case scenario for QuickSort occurs when the pivot chosen at each step is either the smallest or largest element in the remaining unsorted portion of the array. This leads to imbalanced partitions, and the algorithm performs poorly. The worst-case time complexity is \(O(N^2)\), which occurs when the input is already sorted in ascending or descending order.

Average-Case Time Complexity¶

There are many ways to avoid the worst case of quicksort, like choosing the element from the middle of the array as pivot, randomly generating a pivot for each subarray, selecting the median of the first, last, and middle element as pivot, etc. By using these methods, we can ensure equal partitioning, on average. Thus, quick sort's average case time complexity is O(NlogN)

Space Complexity¶

The Space Complexity in quick sort will be because of recursion space. Partition function doesn't take any extra space.

So, space in Quick Sort is only because of Recursion Stack whereas in Merge Sort, the extra space is also taken by Merge Fucntion.

In Quick Sort,

In worst case, Space is O(N) since in recursive tree we have N levels.

In best case, Space is O(log N) since there are log N levels.

Randomised QuickSort¶

The randomised quicksort is a technique where we randomly pick the pivot element, not necessarily the first and last.

There is a random function available in all the languages, to which we can pass Array and get random index. Now, we can swap random index element with first element and execute our algorithm as it is.

Why picking random element helps?¶

Randomised quicksort help us to get away with the worst case time complexity.

The odds of always choosing the minimum element or maximum element is very low.

Example:

Given N elements, probablity that a random element is minimum - 1/N
Probability that again next time the random element is munimum - 1/N-1
Then,.. 1/N-2
Then,.. 1/N-3...

1/N * 1/N-1 * 1/N-2 * .....
1/N!

This value is very small!!

Hence, using randomised quick sort, we can achieve average case of O(N logN) most of the time.

Comparator¶

In programming, a comparator is a function that compares two values and returns a result indicating whether the values are equal, less than, or greater than each other.
The comparator is typically used in sorting algorithms to compare elements in a data structure and arrange them in a specified order.

Comparator is a function that takes two arguments.

For languages - Java, Python, JS, C#, Ruby, the following logic is followed.

1. In sorted form, if first argument should come before second, -ve value is returned.
2. In sorted form, if second argument should come before first, +ve value is returned.
3. If both are same, 0 is returned.

For C++, following logic is followed.

1. In sorted form, if first argument should come before second, true is returned.
2. Otherwise, false is returned.

Problem 2 Sorting based on factors¶

Given an array of size n, sort the data in ascending order of count of factors, if count of factors are equal then sort the elements on the basis of their magnitude.

Example 1

A[ ] = { 9, 3, 10, 6, 4 }
Ans = { 3, 4, 9, 6, 10 }

Explanation:

Total number of factors of 3, 4, 9, 6, 10 are 2, 3, 3, 4, 4.

Question¶

Given an array A of size n, sort the data in ascending order of count of factors, if count of factors are equal then sort the elements on the basis of their magnitude.

A = [10, 4, 5, 13, 1]

Choices

[1, 4, 5, 10, 13]
[1, 5, 13, 4, 10]
[13, 10, 4, 5, 1]
[1, 4, 5, 13, 10]

Explanation:

Total number of factors of 1, 5, 13, 4, 10 are 1, 2, 2, 3, 4.

Sorting based on factors Solutions¶

C++¶

int factors(int n) {
  int count = 0;
  int sq = sqrt(n);

  // if the number is a perfect square
  if (sq * sq == n)
    count++;

  // count all other factors
  for (int i = 1; i < sqrt(n); i++) {
    // if i is a factor then n/i will be
    // another factor. So increment by 2
    if (n % i == 0)
      count += 2;
  }
  return count;
}

bool compare(int val1, int val2) {
  int cnt_x = count_factors(x);
  int cnt_y = count_factors(y);

  if (factors(val1) == factors(val2)) {
    if (val1 < val2) {
      return true;
    }
    return false;
  } else if (factors(val1) < factors(val2)) {
    return true;
  }
  return false;
}

vector < int > solve(vector < int > A) {
  sort(A.begin(), A.end(), compare);
  return A;
}

Python¶

import functools

//please write the code for finding factors by yourself

def compare(v1, v2):
  if (factors(v1) == factors(v2)):
    if (v1 < v2):
      return -1;
if (v2 < v1):
  return 1;
else
  return 0;
elif(factors(v1) < factors(v2)):
  return -1;
else
  return 1;

class Solution:
  def solve(self, A):
  A = sorted(A, key = functools.cmp_to_key(compare))
return A

Java¶

//please write the code for finding factors by yourself

public ArrayList < Integer > solve(ArrayList < Integer > A) {
  Collections.sort(A, new Comparator < Integer > () {
    @Override
    public int comp(Integer v1, Integer v2) {
      if (factors(v1) == factors(v2)) {
        if (v1 < v2) return -1;
        else if (v2 < v1) return 1;
        return 0;
      } else if (factors(v1) < factors(v2)) {
        return -1;
      }
      return 1;
    }
  });
  return A;
}

Problem 3 B Closest Points to Origin¶

Given an array of points where points[i] = [xi, yi] represents a point on the X-Y plane and an integer k, return the B closest points to the origin (0, 0).

The distance between two points on the X-Y plane is the Euclidean distance (i.e., \(√(x1 - x2)^2 + (y1 - y2)^2\)).

You may return the answer in any order.

Example 1:

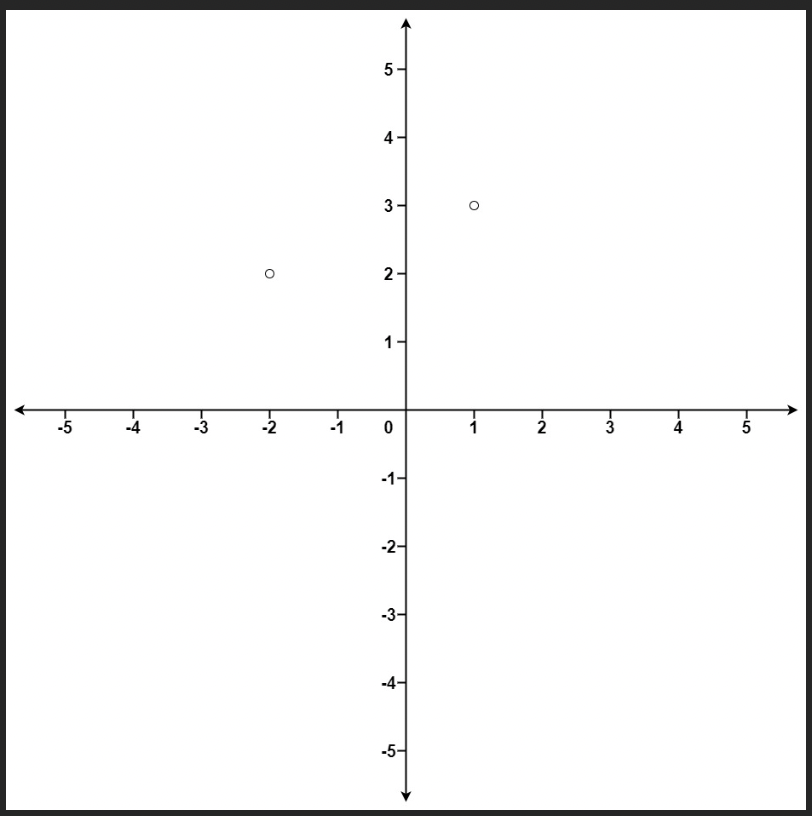
Input: points = [[1,3],[-2,2]], B = 1

Output: [[-2,2]]

Explanation:

The distance between (1, 3) and the origin is sqrt(10).
The distance between (-2, 2) and the origin is sqrt(8).
Since sqrt(8) < sqrt(10), (-2, 2) is closer to the origin.
We only want the closest B = 1 points from the origin, so the answer is just [[-2,2]].

Example 2:

Input: points = [[3,3],[5,-1],[-2,4]], B = 2

Output: [[3,3],[-2,4]]

Explanation: The answer [[-2,4],[3,3]] would also be accepted.

B Closest Points to Origin Approach

We find the B-th distance by creating an array of distances and then sorting them using custom sorting based on distances from origin or points.

After, we select all the points with distance less than or equal to this K-th distance.

Logic for Custom Sorting

Say there are two points, (x1, y1) and (x2, y2),
The distance of (x1, y1) from origin will be \({sqrt((x1-0)^2 + (y1-0)^2)}\)
The distance of (x2, y2) from origin will be \({sqrt((x2-0)^2 + (y2-0)^2)}\)

We can leave root part and just compare \((x1^2 + y1^2) and (x2^2 + y2^2)\)

Below logic works for languages like - Java, Python, JS, ...

// Need to arrange in ascending order based on distance

// If first argument needs to be placed before, negative gets returned
if((x1*x1 + y1*y1) < (x2*x2 + y2*y2))
    return -1;
// If second argument needs to be placed before, positive gets returned
else if ((x1*x1 + y1*y1) > (x2*x2 + y2*y2))
    return 1;
// If both are same, 0 is returned
else return 0
--------------------------------------------- 
// Instead of writing like above, we could have also written

return ((x1*x1 + y1*y1) - (x2*x2 + y2*y2))

Below logic works for C++¶

// If first argument needs to be placed before, true gets returned
if ((x1 * x1 + y1 * y1) < (x2 * x2 + y2 * y2))
  return true;
//Else false is returned
else return false

Problem 4 Largest Number¶

Given a list of non-negative integers nums, arrange them such that they form the largest number and return it.

Since the result may be very large, so you need to return a string instead of an integer.

Example 1:

Input: nums = [10,2]

Output: "210"

Example 2:

Input: nums = [3,30,34,5,9]

Output: "9534330"

Idea:¶

Should we sort the numbers in descending order and append them ?

While it might be tempting to simply sort the numbers in descending order, but this doesn't work.

For example, sorting the problem example in descending order would produce the number 9534303, while the correct answer is achieved by putting 3 before 30.

Question¶

Given a list of non-negative integers nums, arrange them such that they form the largest number and return it.

nums = [10, 5, 2, 8, 200]

Choices

20010825
85220010
88888888
85200210

Explanation:

After rearrangeing the nums, [8, 5, 2, 200, 10] will form the largest number as "85220010".

Warning

Please take some time to think about the solution approach on your own before reading further.....

Larget Number Approach¶

We shall use custom sorting.
Say we pick two numbers X and Y. Now, we can check if X (appends) Y > Y (appends) X, then it means that Y should come before X.

For example, let X and Y be 542 and 60. To compare X and Y, we compare 54260 and 60542. Since 60542 is greater than 54260, we put Y first.

Once the array is sorted, the most "signficant" number will be at the front.

Edge Case

There is a minor edge case that comes up when the array consists of only zeroes, so if the most significant number is 0, we can simply return 0. Otherwise, we build a string out of the sorted array and return it.

Example

Upon sorting this array - [3,30,34,5,9],
we shall get - [9, 5, 34, 3, 30]

Now, we can simply append the numbers to get - 9534330

Complexity¶

Time complexity : O(n log n)

Although we are doing extra work in our comparator, it is only by a constant factor. Therefore, the overall runtime is dominated by the complexity of sort, which is O(n log n).

Space complexity : O(n)

Space depends on the type of algorithm used by the sort function internally.

Larget Number Codes in different langauges¶

C++¶

bool compare(int a, int b) {
  return to_string(a) + to_string(b) > to_string(b) + to_string(a);
}

string largestNumber(vector < int > & A) {
  sort(A.begin(), A.end(), compare);
  string ans = "";
  for (auto & x: A)
    ans += to_string(x);
  if (ans[0] == '0') return "0";
  return ans;
}

Java¶

public class Solution {
  public String largestNumber(ArrayList < Integer > A) {
    Collections.sort(A, new Comparator < Integer > () {
      public int compare(Integer a, Integer b) {
        String XY = String.valueOf(a) + String.valueOf(b);
        String YX = String.valueOf(b) + String.valueOf(a);
        return XY.compareTo(YX) > 0 ? -1 : 1;
      }
    });
    StringBuilder ans = new StringBuilder();
    for (int x: A) {
      ans.append(String.valueOf(x));
    }
    if (ans.charAt(0) == '0')
      return "0";
    return ans.toString();
  }
}

Python¶

from functools import cmp_to_key

class Solution:
    # @param A : list of integers
    # @return a strings
    def largestNumber(self, A):
        def cmp_func(x, y):
            if x + y > y + x:
                return -1
            elif x == y:
                return 0
            else:
                return 1

        nums = [str(num) for num in A]
        nums.sort(key = cmp_to_key(cmp_func))
        if nums[0] == '0':
            return '0'
        return ''.join(nums)

Question¶

Best case TC of quick sort?

Choices

N
N²
N log N
Constant

Question¶

Worst case TC of quick sort?

Choices

N
N²
N log N
Constant

Question¶

Worst case SC of quick sort?

Choices

N
N²
N log N
Constant

Question¶

Best case SC of quick sort?

Choices

N
N²
N log N
log N