Stacks 1: Implementation & Basic Problems¶

Introduction to Stacks with Example¶

Definition¶

A stack is a linear data structure that stores information in a sequence, from bottom to top.
The data items can only be accessed from the top and new elements can only be added to the top, i.e it follows LIFO (Last In First Out) principle.

Examples

Before proceeding to more technical examples, let's start from the real life basic examples.

Pile of Plates:
Imagine a scenario where you have a pile of plates, you can only put a plate on the pile from top also only pick a plate from top. You can't really see the plates underneath the top one without first removing the top plate, which means only the first plate is accessible to you.

Stack of Chairs:
We usually place identical chairs on the top of on another, which makes them look like a stack. Similar to the previous example you can only position or choose a chair from top, and you won't be able to take or see the chair in middle without picking out all chairs on top of that one.

Algorithmic Examples¶

Recursion:
Recursion happens when a function calls itself. Each call is stacked on top of the previous one. When call execution finishes, control goes back to the second-to-last function call. This all happens with a stack data structure.
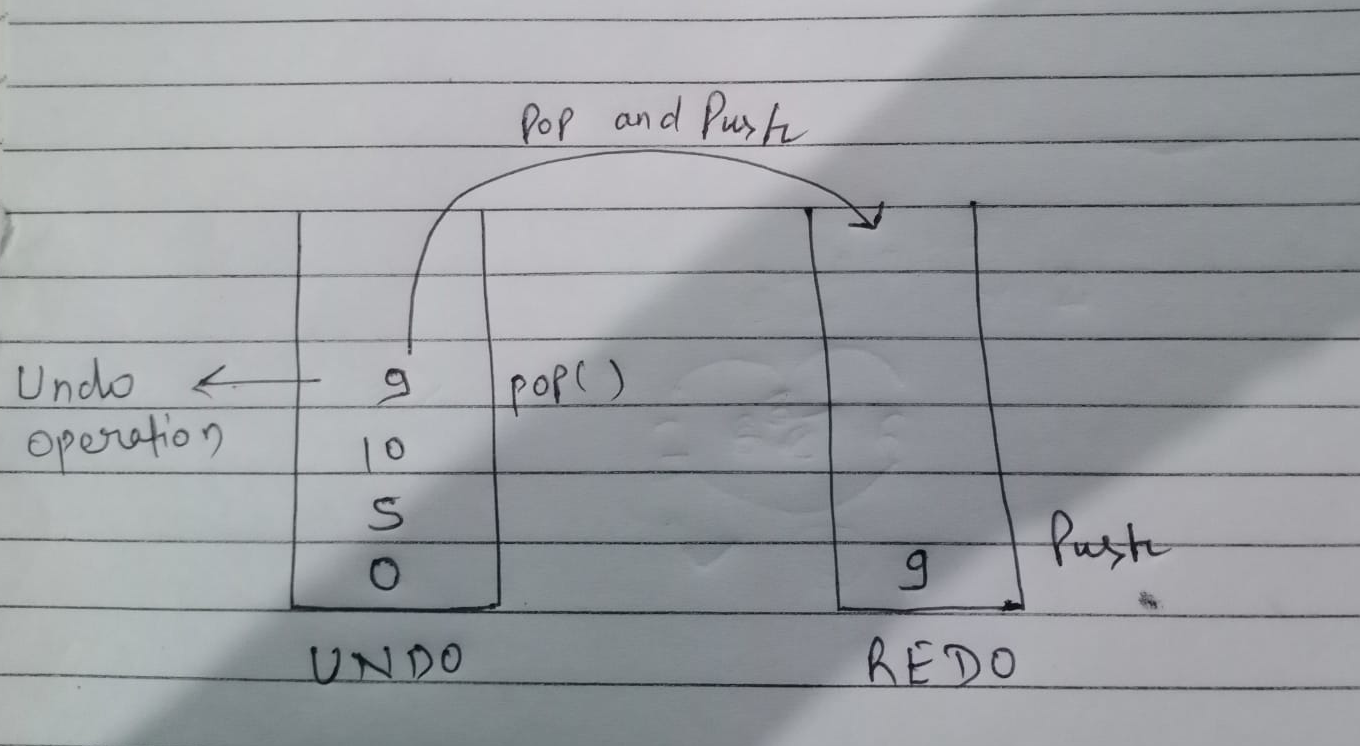
Undo / Redo Operations:
In software programs, stacks are commonly used to store the state during Undo and Redo operations. Consider the given example we have performed several calculations here, our first stack stores the current state. As soon as user performs UNDO operation the state is moved to REDO stack so that later it can be restored from there.

Question¶

What is the most common application of a stack?

Choices

Evaluating arithmetic expressions
Implementing undo/redo functionality
Representing parenthesis in expressions
All of the above

Answer: All of the above

Explanation: Stacks are versatile data structures that find applications in various domains. They are commonly used in expression evaluation, undo/redo functionality, and representing parenthesis in expressions.

Operations on Stack¶

These operations are generally used on the stack. The time complexity for all of these operations is constant O(1).

1. Push¶

Push operation is to insert a new element into the top of stack.

push(data)

2. Pop¶

Pop operation is to remove an element from the top of stack.

pop()

3. Peek¶

Peek means to access the top element of the stack, this operation is also called as top.

data = peek() 
// or
data = top()

4. isEmpty¶

This operation is used to check whether stack is empty or not. It is an important operation because it allows program to run efficiently by checking conditions of overflow and underflow.

isEmpty()

Question¶

What is the time complexity of the push and pop operations in a stack?

Choices

O(1) for both push and pop
O(n) for push and O(1) for pop
O(1) for push and O(n) for pop
O(n) for both push and pop

Answer: O(1) for both push and pop

Explanation: The push and pop operations in a stack operate on the top element, making them constant time operations. This is because the top element is always accessible regardless of the stack's size.

Implement Stack using Arrays¶

Just try to think what a data structure is, a data structure is nothing but a way to store some data in memory along with some rules to insert/access/modify that data.
So, stacks is also a way to store data with LIFO principle. The conclusion of this is we can implement stacks by using arrays.
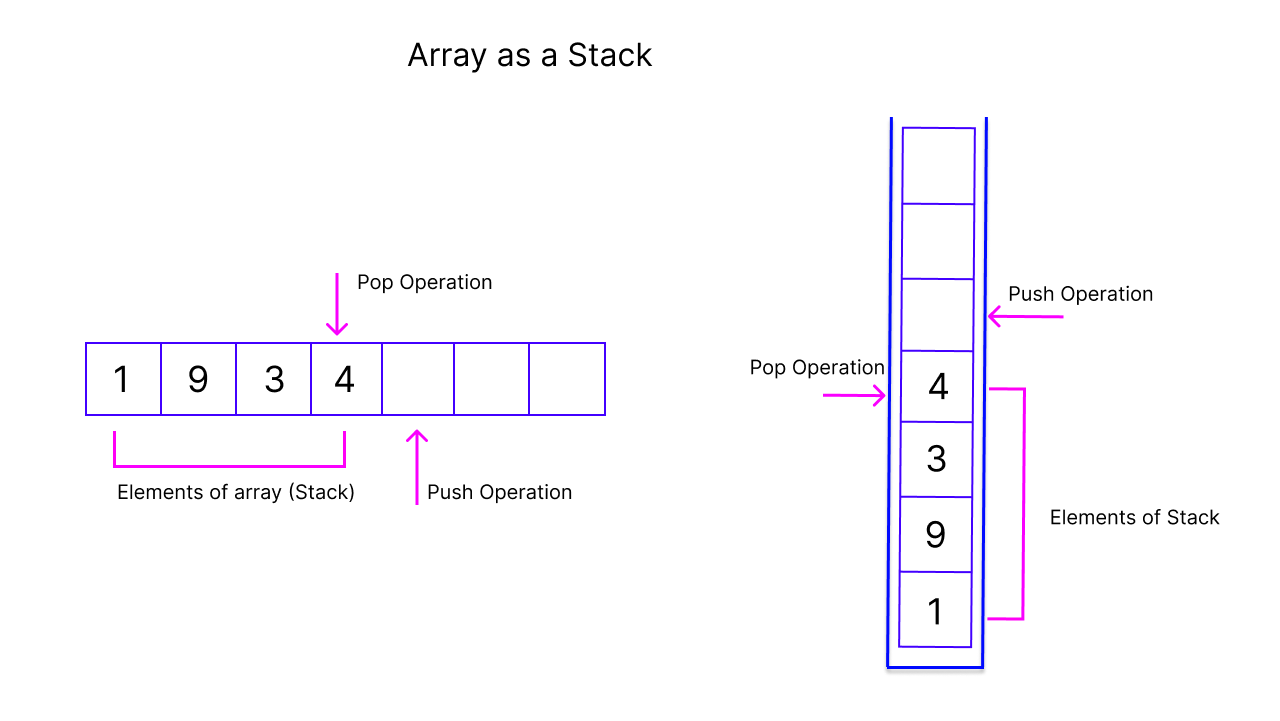
You might know that array is filled from left to right so the rightmost part of the array can act as top of stack, for each pop operation we can remove the rightmost element from array.
We can keep track of the top element index in array because we can always know how many elements we have inserted so directly access that index from array to know about top element.
To store an element we can just add 1 to top index and assign the element.

Pseudocode¶

// Consider an array `A`.
int A[];

// Consider a counter to keep track of stack size and currently used index
int t = -1;

For push operation we can keep pushing data from left to right.

void push(data){
    t++;
    A[t] = data;
}

And as we are maintaining a counter we can always access the top element in O(1) by just index access of array.

int top(){
    return A[t];
}

To remove element we can simply decrement our counter. Also we can place some value at that index to denote that it is not part of our data.

void pop(){
    t--;
}

We are maintaining our counter in such a way that it indicates the size of stack. We can simply perform an equality check on counter to know whether stack is empty.

bool isEmpty(){
    return t == -1;
}

Overflow and Underflow in stack and it's solution¶

Overflow occurs when we try to store new data even when there is no empty space in array. For this we have to introduce a overflow condition before push operation.

void push(x){
    // Whenever our counter reaches to the size of the array 
    // It means stack is already full
    if(t >= A.size())
        return;
    t++;
    A[t] = x;
}

Underflow means when we try to perform pop operation or try to access the element of stack but there are none. Again we have to introduce conditions during pop and top operation.

void pop(){
    if(!isEmpty()) return;
    t--;
}

int top(){
    if(!isEmpty()) return -1;
    return A[t];
}

Problem with implementation using Arrays¶

We have to predefine the size of stack to create array. To overcome this problem we can create a dynamic array which can grow or shrink at runtime according to need.

Question¶

What happens when you try to pop an element from an empty Stack?

Choices

It returns null
It returns the top element
It causes an underflow
It causes an overflow

Attempting to pop an element from an empty stack will cause an underflow.

Implement Stack using Linked List¶

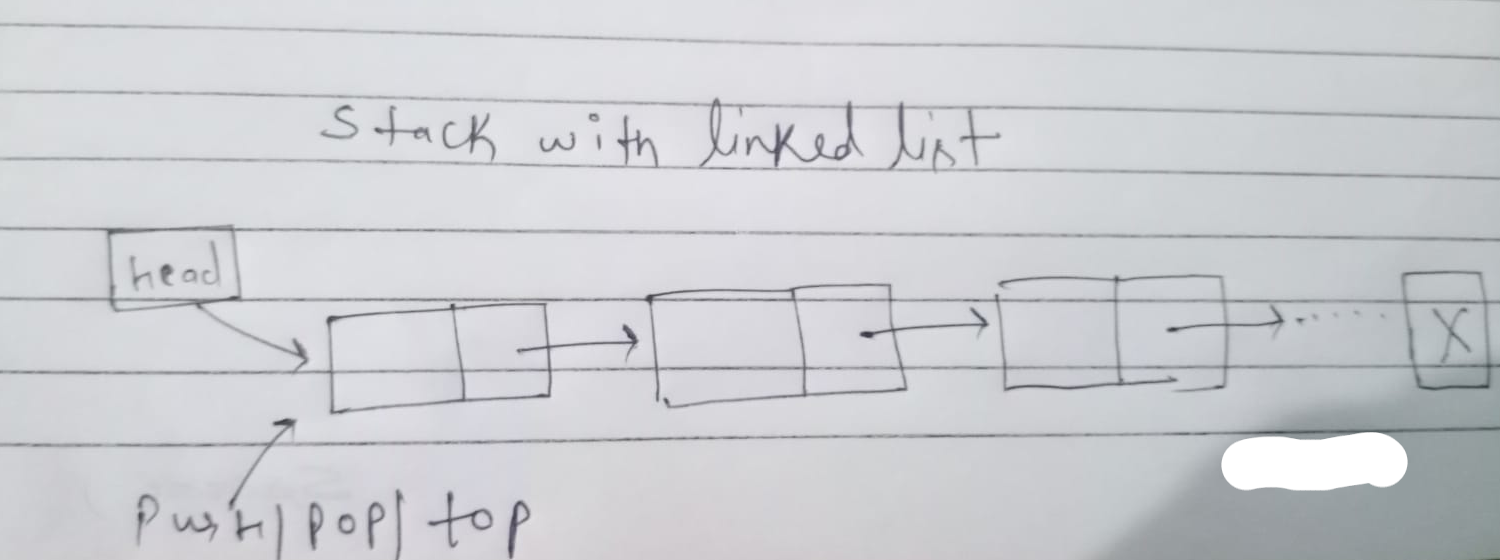
We can also implement stack using linked list, similar to the array it also has constant O(1) time complexity for all operations.
We choose head as our top element because push and pop operations can be executed in O(1) in that case.
Unlike array linkedlist can grow or shrink at runtime, because all operations are performed at head.

Pseudocode¶

To push data into stack, just create a node and attach before head.

void push(data) {
  new_node = Create a new Node with 'data'
  new_node.next = head
  head = new_node
  // Increment size
  t++
}

To pop data just remove one node from the beginning of linked list.

void pop() {
  if (!isEmpty()) return;
  head = head.next
  // Decrement size
  t--
}

To find the data on top just access the head node.

int top() {
  if (!isEmpty()) return -1;
  return head.data;
}

Note: While accessing top value in function, We can use another concept to indicate that stack is empty if we are using -1 as value to store in stack.

Problem 3 Balanced Paranthesis Concept with Implementation¶

Check whether the given sequence of parenthesis is valid ?

Explanation of Problem¶

Imagine you have a bunch of different types of brackets, like { and } (curly brackets), [ and ] (square brackets), and ( and ) (round brackets).

A valid sequence of these brackets means that for every opening bracket, there is a matching closing bracket. It's like having pairs of shoes; you need a left shoe and a right shoe for each pair. In a valid sequence, you have the same number of left and right brackets, and they are correctly matched.

For example, (({})) is a valid sequence because for each opening bracket ( or {, there is a corresponding closing bracket ) or }.

On the other hand, {{}) is not valid because the second curly bracket } doesn't have a matching opening bracket, so it's like having an extra right shoe without a left shoe to match with.

In summary, a valid sequence of brackets is like having balanced pairs of brackets, where each opening bracket has a matching closing bracket.

Technical Application -

Imagine you are writing a small compiler for your college project and one of the tasks (or say sub-tasks) for the compiler would be to detect if the parenthesis are in place or not.

Question¶

Which of the following expressions is balanced with respect to parentheses?

Choices

(a + b) * c
(a + b)) * c
(a + b)(c
(a + b)c

Balanced Parenthesis Implementation¶

Idea¶

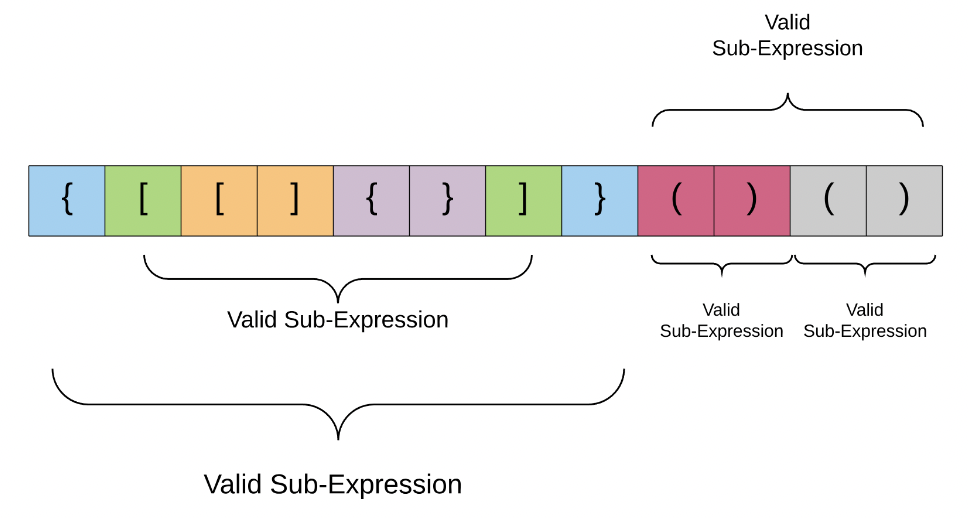
An interesting property about a valid parenthesis expression is that a sub-expression of a valid expression should also be a valid expression. (Not every sub-expression) e.g.

Hint¶

What if whenever we encounter a matching pair of parenthesis in the expression, we simply remove it from the expression?

The stack data structure can come in handy here in representing this recursive structure of the problem. We can't really process this from the inside out because we don't have an idea about the overall structure. But, the stack can help us process this recursively i.e. from outside to inwards.

Warning

Please take some time to think about the solution approach on your own before reading further.....

Approach¶

Iterate through the sequence, and whenever you encounter an opening parenthesis, you push it onto the stack.
When you encounter a closing parenthesis, you pop the top element from the stack and compare it to the current closing parenthesis. If they are of the same type (matching), you continue; otherwise, the sequence is invalid.

Additionally, if you finish iterating through the sequence and the stack is not empty, the sequence is also invalid.

Pseudocode¶

bool is_valid_parentheses(sequence):
    // Initialize an empty stack

    For each character 'char' in sequence:
        If 'char' is an opening parenthesis ('(', '{', '['):
            Push 'char' onto the stack
        Else if 'char' is a closing parenthesis (')', '}', ']'):
            If the stack is empty:
                Return false
            Pop the top element from the stack into 'top'
            If 'top' is not of the corresponding opening type for 'char':
                Return false

    If the stack is not empty:
        Return false
    Else:
        Return true

Dry Run¶

Example: {()[]}

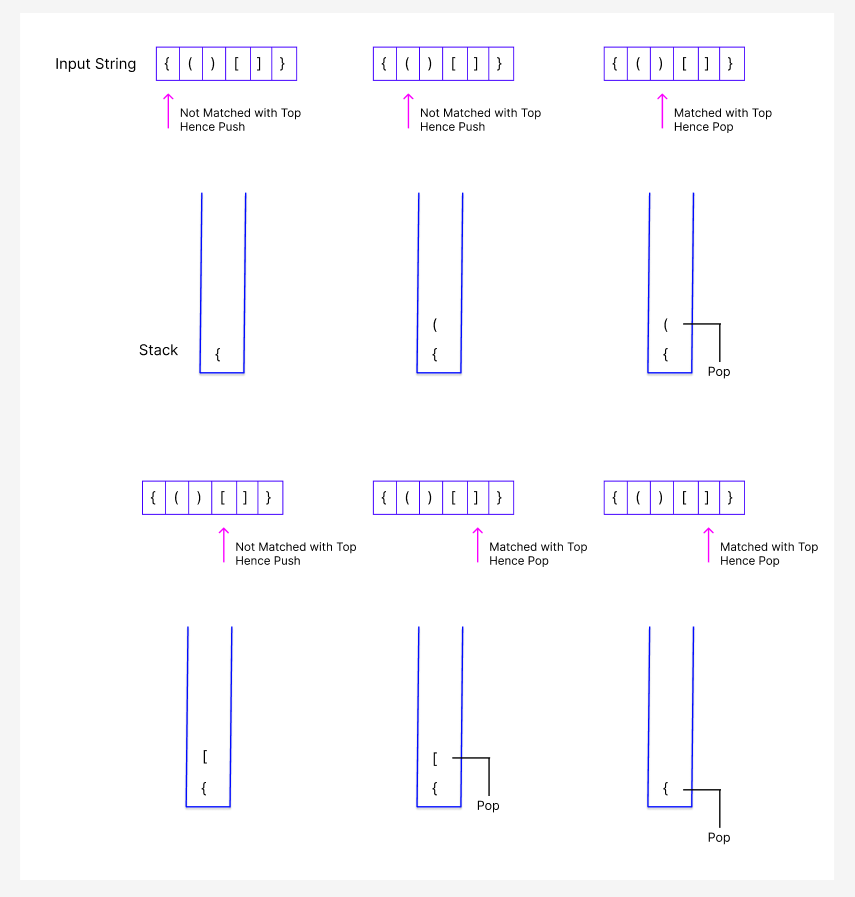
Iterate on the example string.
First of all we will encounter {. We will push it onto the stack.
Next we have ( again push onto the stack.
Now when we encountered ), It means there is a match so pop the top element and continue the iteration.
In next iteration we will encounter [. Similarly we will find the closing bracket in next iteration ]. Pop that from stack.
In the end stack will only contain {. Now when we will encounter }, we will again pop the topmost bracket.
Finally there is nothing to iterate on as well as the stack is now empty. Which means the paranthesis sequence was valid.

Problem 4 Remove equal pair of consecutive elements till possible¶

Given a string, remove equal pair of consecutive elements till possible

Example

Let's say we have a string like abcddc, The idea here is to check if there are any consecutive pairs of characters that are the same. In this case, we see dd is such a pair. When you find such a pair, you simply remove it from the string, and it becomes abcc Then, you repeat the process with the new string, searching for and removing consecutive matching pairs of letters. This cycle continues until there are no more matching pairs left to remove.

In the end the final string would be the solution.

Approach

This problem can be solved very efficiently by using the concept of stack. The stack will help you keep track of the elements that haven't been canceled out by a matching element.

string remove_equal_pairs(s):
    Initialize an empty stack

    For each character 'char' in s:
        If the stack is not empty and 'char' matches the character at the top of the stack:
            Pop the element from the stack
        Else:
            Push 'char' onto the stack

    Initialize an empty string 'result'

    While the stack is not empty:
        Pop an element from the stack and prepend it to 'result'

    Return 'result'

Complexity¶

Time Complexity: O(n)
Space Complexity: O(n)

Question¶

If we remove equal pair of consecutive characters in this string multiple times then what will be the final string: abbcbbcacx

Choices

empty string
ax
cx
x

Explanation:

Let's go through the step-by-step process for the given example: abbcbbcacx.

Begin by pushing a onto the stack: Stack - [a]
Next, push b onto the stack: Stack - [a, b]
During the next iteration, we will encounter b which matches the top element b of the stack. Continue iterating with a pop operation. Stack - [a]
Proceed to push c during the next iteration, followed by b. Stack - [a, c, b]
During the subsequent iteration, encountering b matches the top element of the stack. Since a consecutive pair is found, perform a pop operation to remove the topmost character, which is b. Stack - [a, c]
As we encounter c again, and another c is already at the top of stack, pop c and continue iterating. Stack - [a]
The stack now contains only a. In the next iteration, encountering a leads to a pop operation for the existing a. Stack - []
Towards the end, push c and x onto the stack. Since there's no more to continue, the final stack [c, x], represents the answer.

Problem 5 Evaluate Postfix Expression¶

Given a postfix expression, evaluate it.

Postfix Expression contains operator after the operands.

Below is an example of postfix expression:

2 + 3 => Postfix => 2 3 +

Idea¶

An operator is present after the operands on which we need to apply that operator, hence stack is perfect data structure for this problem.

Warning

Please take some time to think about the solution approach on your own before reading further.....

We'll process the expression as follows-

Example 1

[2, 3, +]

First we push 2 on stack.
Then we push 3.
Then we found '+', so we will pop top two operands, i.e 3 & 2 in this case
Final result is 2 + 3 = 5

Example 2

[4, 3, 3, *, +, 2, -]

First we push 4 on stack.
Then we push 3 and again 3.
Then we found ' * ', so we will pop top two operands, i.e 3 & 3 in this case and push 3 * 3 to the stack. So push 9.
Again we found '+', so pop the top two operands 9 and 4. Apply '+' operator 9 + 4 = 13 and push into the stack. Push 13.
Push 2.
Now we have an operator again '-', hence pop top two operands and push the result on the stack. 13-2 = 11. Push 11.
In the end the single operand on the stack will be our final answer which is 11.

Question¶

What is the final answer obtained using the stack-based evaluation algorithm for the expression [5, 2, *, 3, -]?

Choices

8
13
7
15

Explanation:

Push 5 onto the stack. Stack: [5]
Push 2 onto the stack. Stack: [5, 2]
Encountering '*' - Pop the top two operands (2 and 5), and push the result (2 * 5 = 10) onto the stack. Stack: [10]
Push 3 onto the stack. Stack: [10, 3]
Encountering '-' - Pop the top two operands (3 and 10), and push the result (10 - 3 = 7) onto the stack. Stack: [7]
Therefore, the final answer obtained using the stack-based evaluation algorithm for the expression [5, 2, *, 3, -]is 7.

Question¶

Evaluate the given postfix expression:

3 5 + 2 - 2 5 * -

Choices

0
4
-4
8

Explanation:

Let's evaluate the given postfix expression step by step: 3 5 + 2 - 2 5 * -

Push 3 onto the stack: Stack - [3]
Push 5 onto the stack: Stack - [3, 5]
Encounter '+', pop 5 and 3, perform 3 + 5 = 8, push 8 onto the stack: Stack - [8]
Push 2 onto the stack: Stack - [8, 2]
Encounter '-', pop 2 and 8, perform 8 - 2 = 6, push 6 onto the stack: Stack - [6]
Push 2 onto the stack: Stack - [6, 2]
Push 5 onto the stack: Stack - [6, 2, 5]
Encounter '*', pop 5 and 2, perform 2 * 5 = 10, push 10 onto the stack: Stack - [6, 10]
Encounter '-', pop 10 and 6, perform 6 - 10 = -4, push -4 onto the stack: Stack - [-4]
End of the expression, the stack contains the final result: -4
So, the result of the expression 3 5 + 2 - 2 5 * - is -4.

Evaluate Postfix Expression Pseudocode¶

Pseudocode¶

int evaluate_postfix(expression):
    Initialize an empty stack

    For each element 'element' in expression:
        If 'element' is an operand:
            Push 'element' onto the stack
        Else if 'element' is an operator:
            Pop 'operand2' from the stack
            Pop 'operand1' from the stack
            Perform the operation 'element' on 'operand1' and 'operand2'
            Push the result back onto the stack

    The final result is at the top of the stack
    Pop and return the result

Complexity¶

Time Complexity: O(n)
Space Complexity: O(n)