Count Sort & Merge Sort¶

Count Sort¶

Find the smallest number that can be formed by rearranging the digits of the given number in an array. Return the smallest number in the form an array.

Example:

A[ ] = {6, 3, 4, 2, 7, 2, 1}
Answer: {1, 2, 2, 3, 4, 6, 7}

A[ ] = {4, 2, 7, 3, 9, 0}
Answer: {0, 2, 3, 4, 7, 9}

Observation/Hint¶

we can to construct a number using digits. The digits in a number can only range from 0 to 9, thus instead of sorting the number which takes O(N log N) time, one can leverage this fixed range to derive a faster solution.

Approach¶

Frequency Count: Create an array of size 10 to count the frequency of each digit in the given number.
Using the frequency array, reconstruct the original array in ascending order.
This method of sorting based on frequency counting is often called "Count Sort".

Pseudocode¶

Frequency Array of size 10
F = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]

for i -> 0 to(N - 1) {
  F[A[i]]++
}

k = 0

for d -> 0 to 9 { // For each digit
  for i -> 1 to F[d] {
    A[k] = d
    k++
  }
}

return A

Dry Run¶

A = [1, 3, 8, 2, 3, 5, 3, 8, 5, 2, 2, 3] (Given Array)
F = [0, 1, 3, 4, 0, 2, 0, 0, 2, 0] (Frequency Array)
Reconstructing A using F: 1 (once), 2 (three times), 3 (four times), 5 (two times), 8 (two times)
Resulting A = [1, 2, 2, 2, 3, 3, 3, 3, 5, 5, 8, 8]

TC and SC¶

Time Complexity: O(N)
Space Complexity: O(1) (Since the size of the frequency array is constant, regardless of the size of N).

Count Sort on large values¶

Will Count Sort work if the range of A[i] is more than \(10^9\)?¶

Count Sort isn't suitable for a range of \(10^9\) because a frequency array of this size would demand too much memory.
Count Sort works well when the range of A[i] is ~ \(10^6\).

Each integer typically occupies 4 Bytes.

Storing \(10^9\) integers requires 4GB, which is often impractical. An array up to \(10^6\) in length is more manageable, needing 4MB.

Count Sort on Negative Numbers¶

Implement Count Sort for an array containing negative numbers.

Observation/Hint¶

Unlike conventional Count Sort, which operates on non-negative integers, this variation needs to account for negative numbers. The method involves adjusting indices in the frequency array based on the smallest element in the original array.

Warning

Please take some time to think about the solution approach on your own before reading further.....

Approach¶

Find Range: Determine the smallest and largest elements in the array to ascertain the range.
Adjust for Negative Numbers: By adjusting indices in the frequency array based on the smallest element, negative numbers can be accounted for.

Example

Given A = [-2, 3, 8, 3, -2, 3]
Smallest = -2, Largest = 8
Range = 11 (8 - (-2) + 1)
Frequency array F = [2, 0, 0, 3, 0, 0, 0, 0, 1]
0^th index frequency is mapped with -2, 1^st index with -1, and so on.
Reconstructed A using F: -2, -2, 3, 3, 3, 8

Pseudocode¶

//Find smallest and largest elements in A
//Create a frequency array F of size (largest - smallest + 1)

for i -> 0 to(N - 1) {
  F[A[i] - smallest_element]++
}

//Reconstruct array A using F

for each index i in F {
  while F[i] > 0 {
    Append(i + smallest_element) to A
    F[i]--
  }
}

TC and SC¶

Time Complexity (TC): O(N)
Space Complexity (SC): O(N + Range)

Merge two sorted arrays¶

Giver an integer array where all odd elements are sorted and all even elements are sorted. Sort the entire array.

A[] = {2, 5, 4, 8, 11, 13, 10, 15, 21}

Approach¶

We can take two separate arrays to keep even(EVEN[]) and odd(ODD[]) elements. Then we can merge them in the original array.

We will keep three pointers here: a(for original array), e(for even array) and o(for odd array), all starting at index 0.

If A[a] is odd, ODD[o]=A[a], o++, a++
If A[a] is even, EVEN[e]=A[a], e++, a++

Pseudocode¶

void merge(A[]) {
  int N = A.length();
  //n1: count of even elements
  //n2: count of odd elements
  int EVEN[n1], ODD[n2];
  int a = 0, e = 0, o = 0;

  for (int i = 0; i < N; i++) {
    if (A[a] % 2 == 0) {
      EVEN[e] = A[a];
      e++;
    } else {
      ODD[o] = A[a];
      o++;
    }
    a++;
  }

  a = 0; // moves over A
  e = 0; // moves over EVEN
  o = 0; // moves over ODD

  while (e < n1 && o < n2) {
    if (EVEN[e] < ODD[o]) {
      A[a] = EVEN[e];
      e++;
    } else {
      A[a] = ODD[o];
      o++;
    }
    a++;
  }

  while (e < n1) {
    A[a] = EVEN[e];
    e++;
    a++;
  }

  while (o < n2) {
    A[a] = ODD[o];
    a++;
    o++;
  }
}

Question¶

Iteration of merging 2 Arrays?

Choices

N ^ 3
N ^ 2
2 * N
Constant

Merge Sort¶

Example: Sorting Examination Sheets¶

A teacher collected the examination sheets of students randomly. Now, she needs to sort those sheets as per roll number of students. As she is smart, instead of sorting it by herself, she divided the sheets into two halves and gave each half to Kishore and Suraj for sorting.

Once she has the sorted halves, she just need to merge two sorted halves, which is significantly easier.

Kishore and Suraj also decided to repeat this and divided the sheets in two halves and gave them to their friends for sorting.

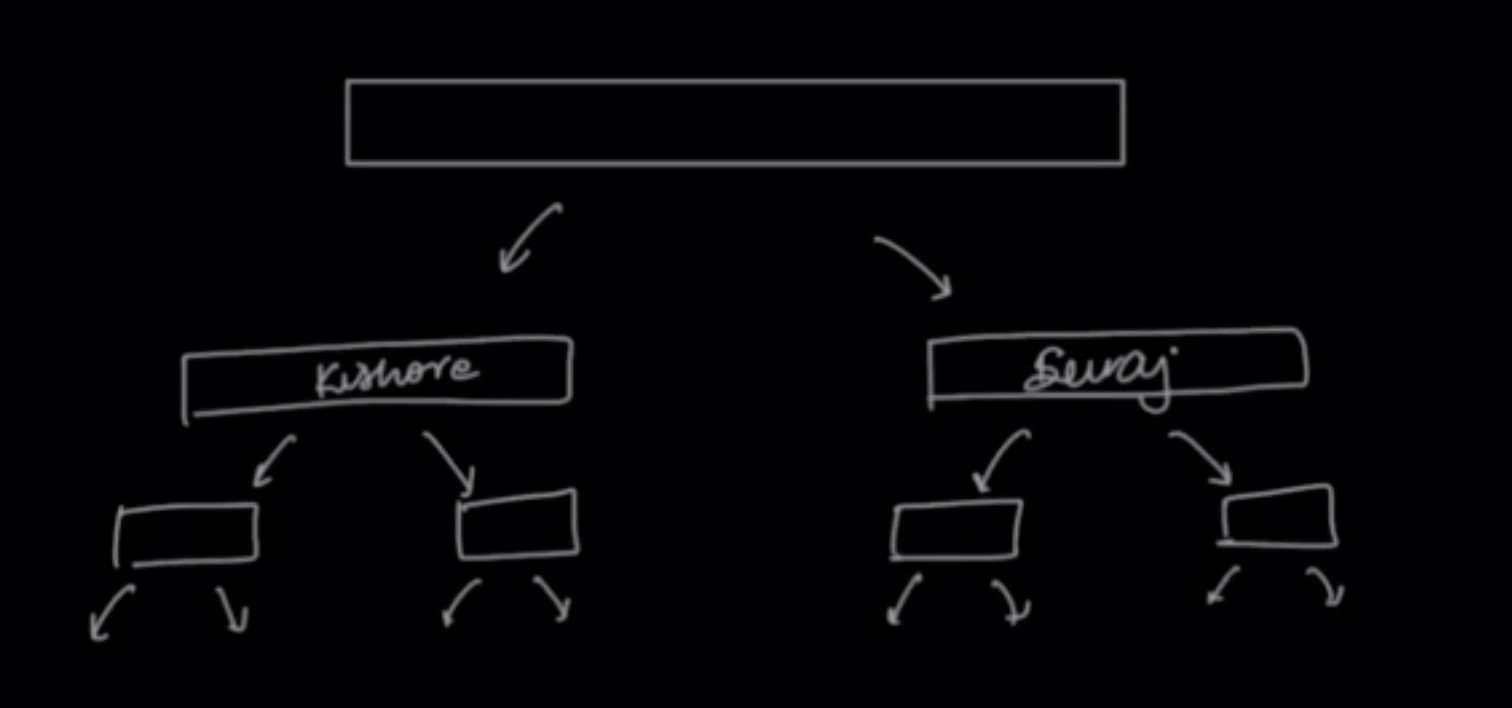
In this way, the last students will have one sheet only. They can directly gave that sheet to the students before them whose job will be to arrange those two sheets and pass it above.

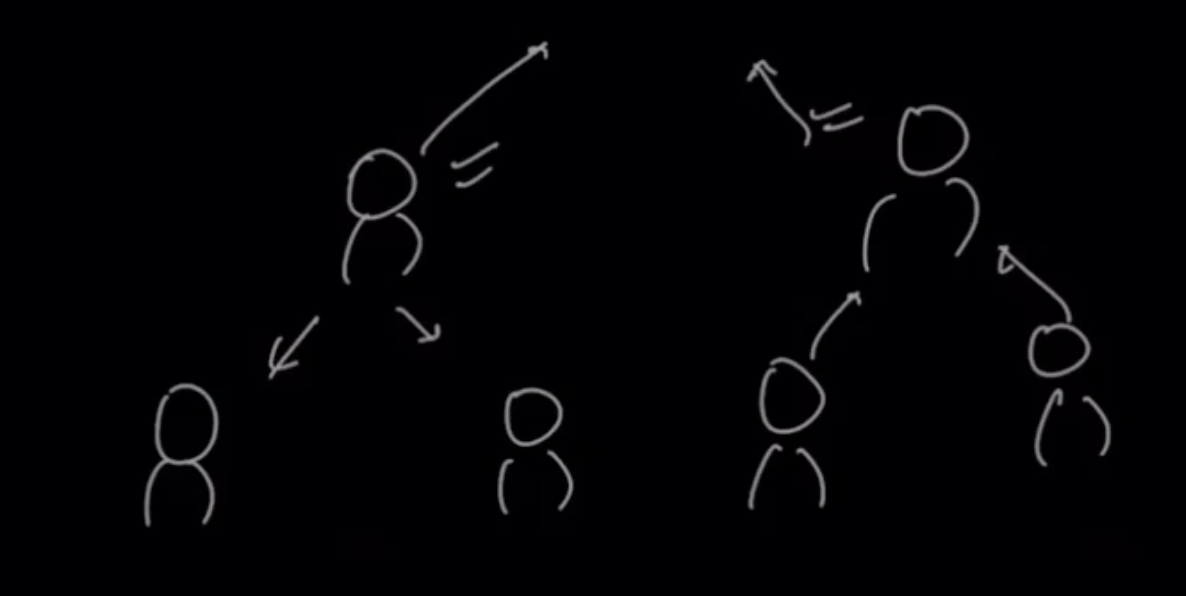
In this way, the sheets are finally sorted.

Example: Sorting Numbers

Sort the array, A = {3, 10, 6, 8, 15, 2, 12, 18, 17}

Divide¶

The idea is to divide the numbers in two halves and then start merging the sorted arrays from bottom and pass above.

Merge¶

Merging [3] and [10] as [3, 10]

Merging [3, 10] and [6] as [3, 6, 10]

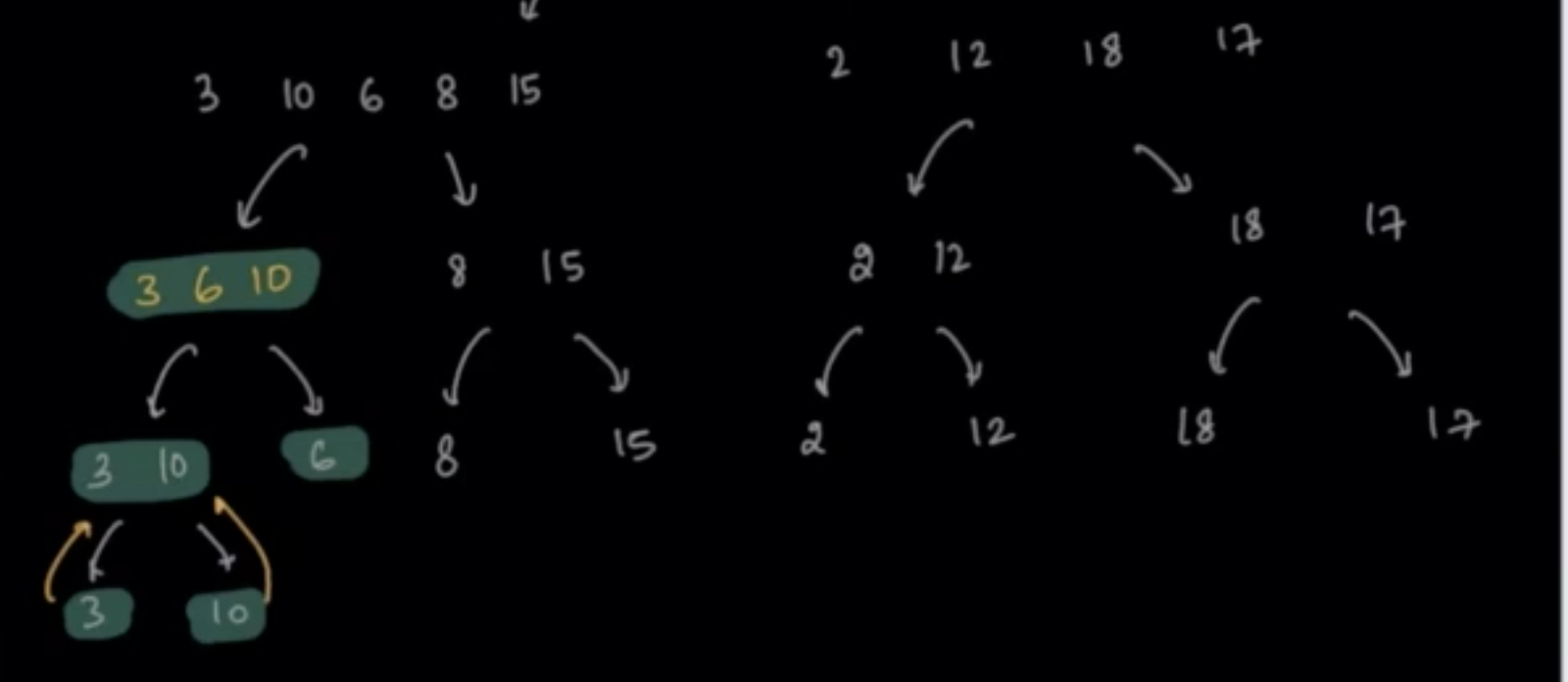
Merging [8] and [15] as [8, 15]

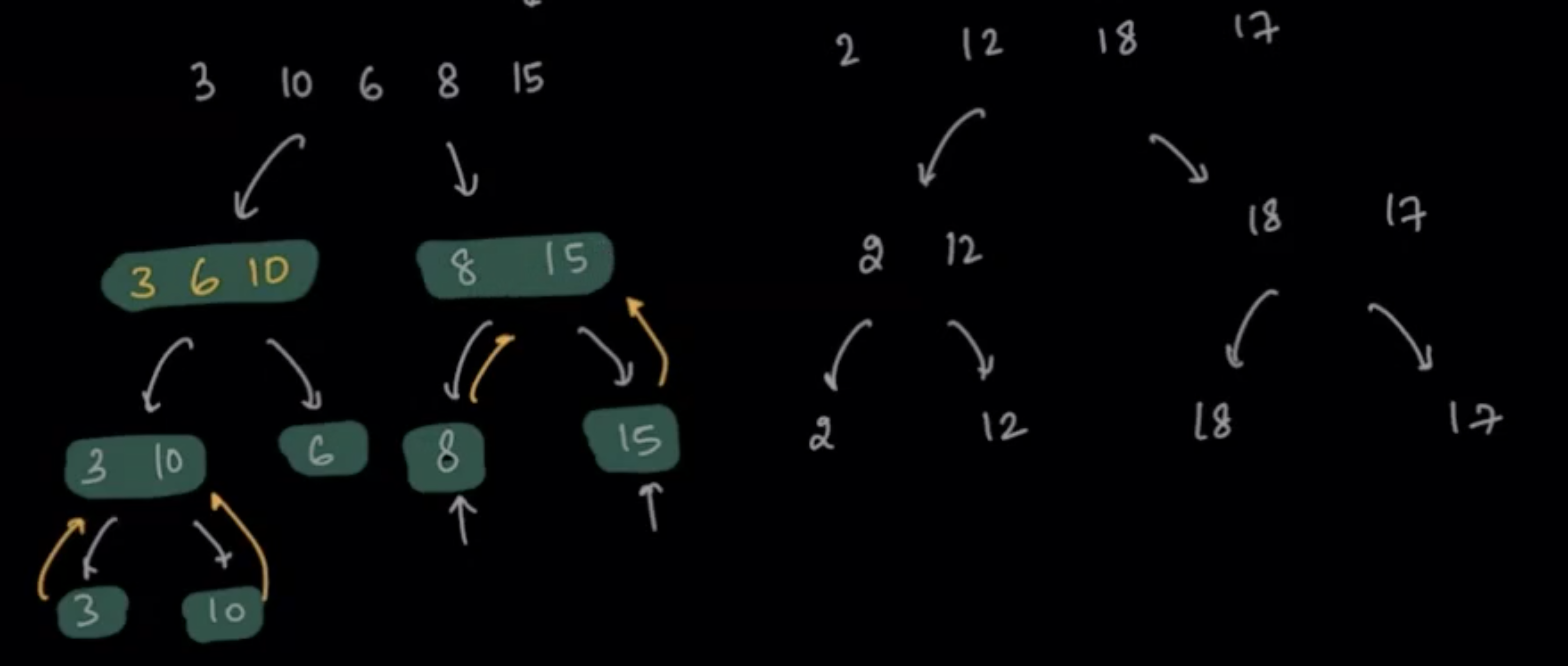
Merging [3, 6, 10] and [8, 15] as [3, 6, 8, 10, 15]

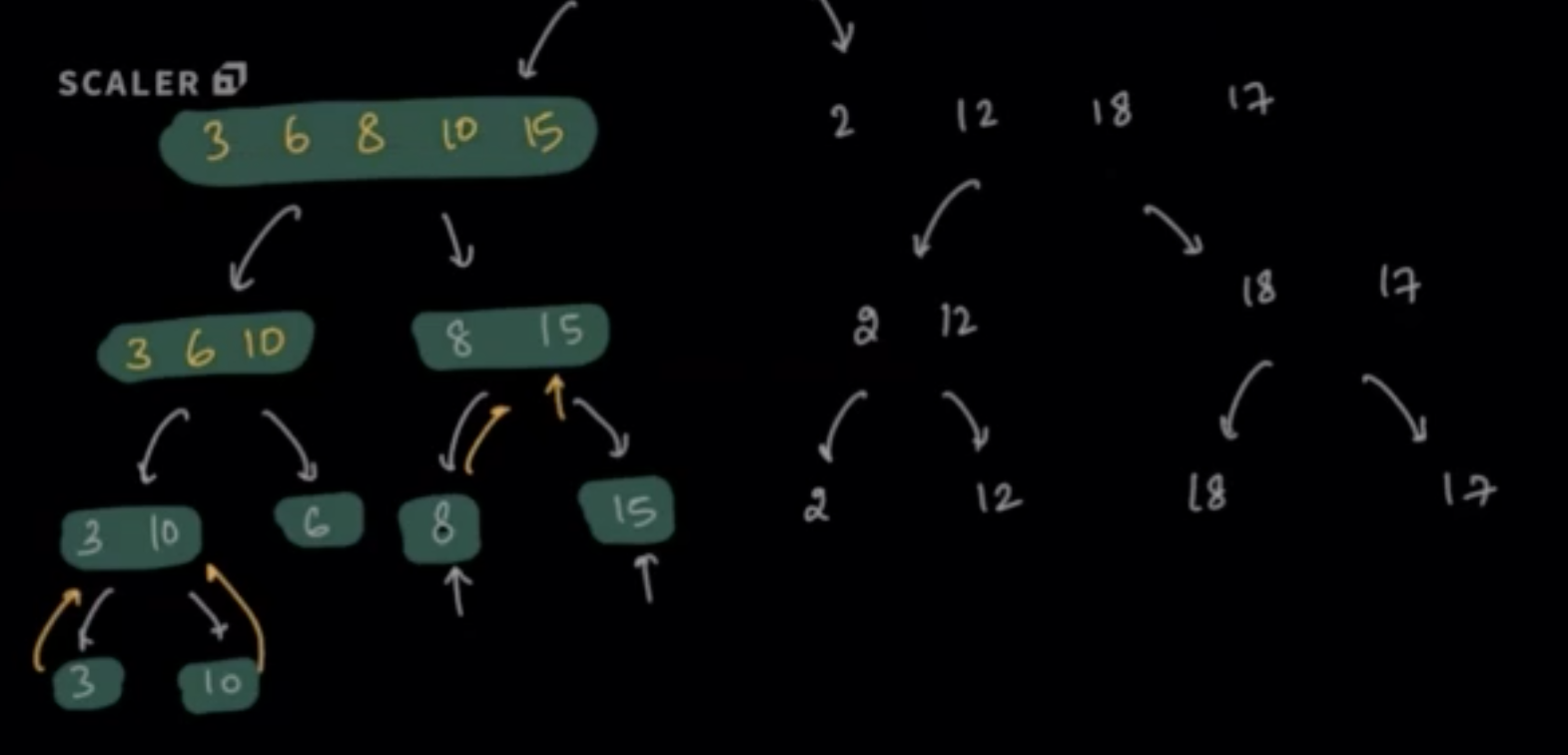
Merging [2] and [12] as [2, 12]

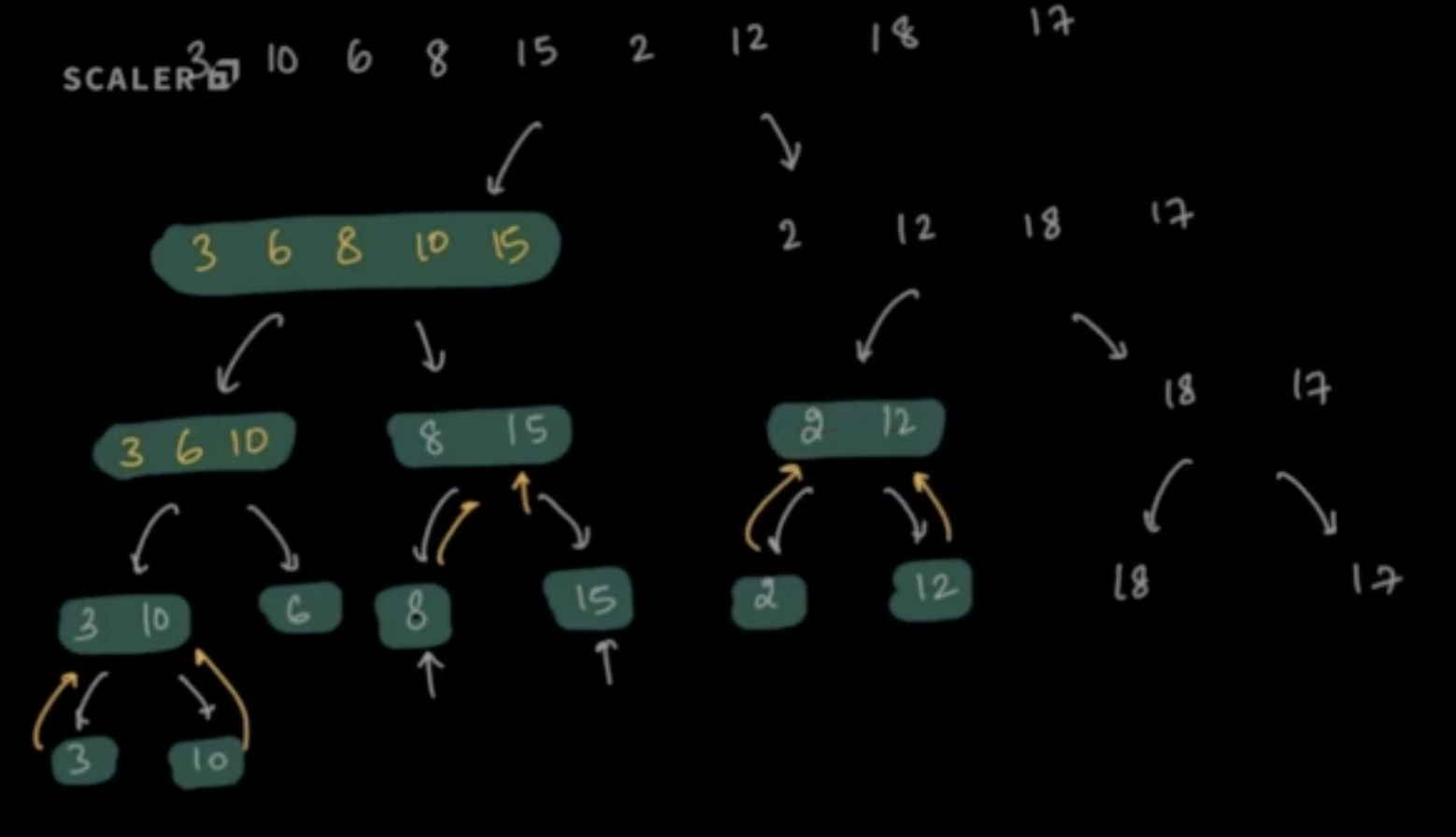
Merging [18] and [17] as [17, 18]

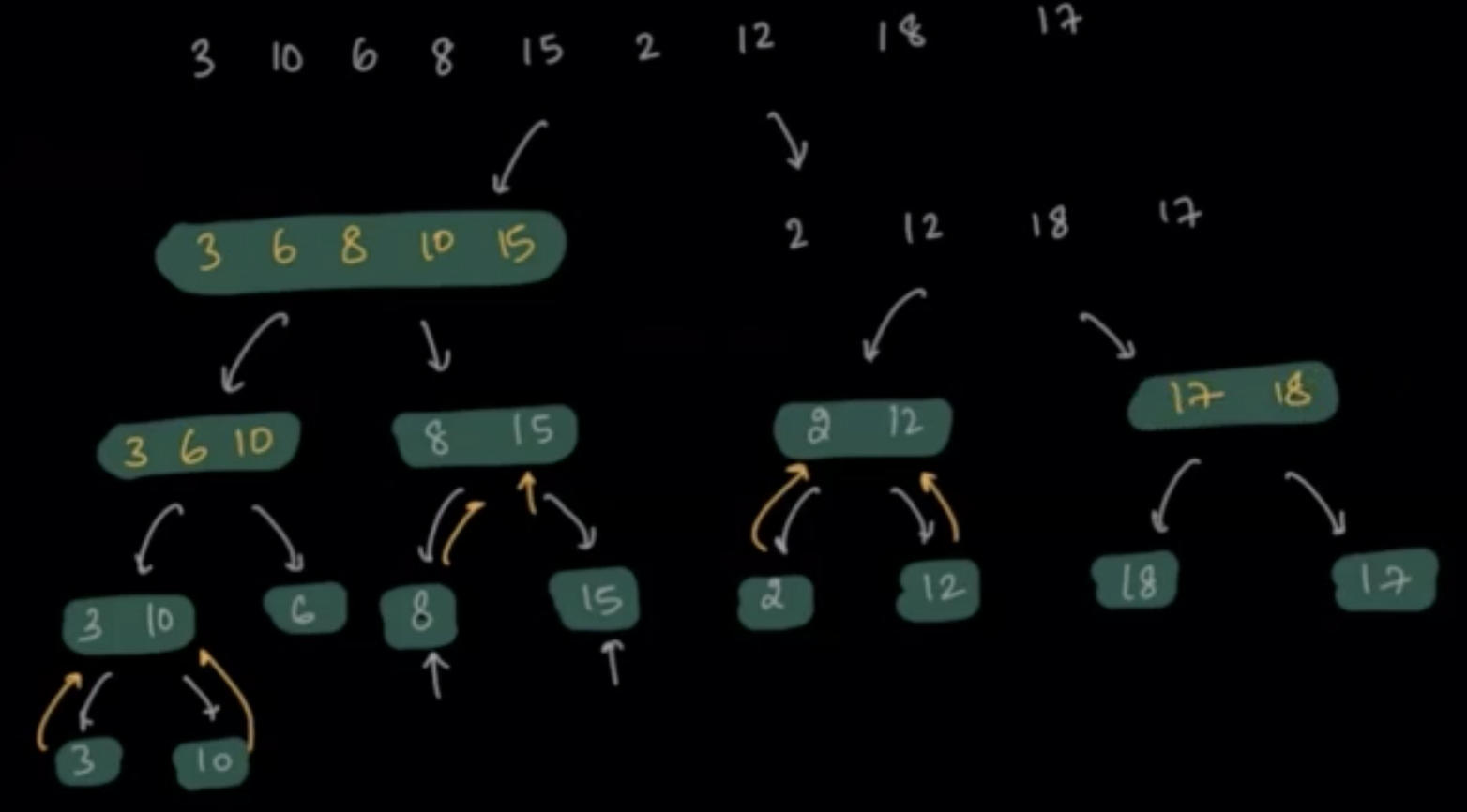
Merging [2, 12] and [17, 18] as [2, 12, 17, 18]

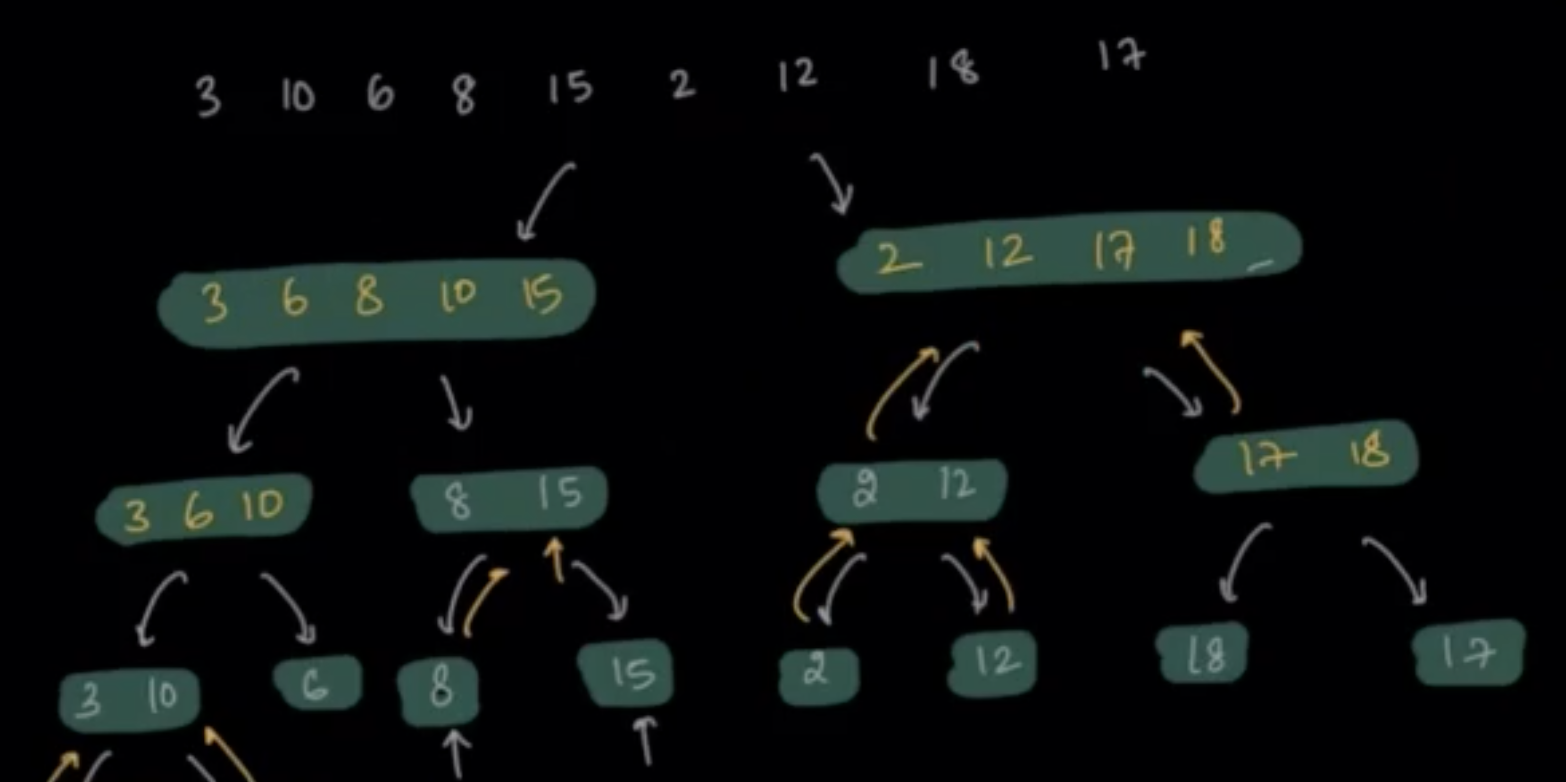
Merging [3, 6, 8, 10, 15] and [2, 12, 17, 18] as [2, 3, 6, 8, 10, 12, 15, 17, 18]

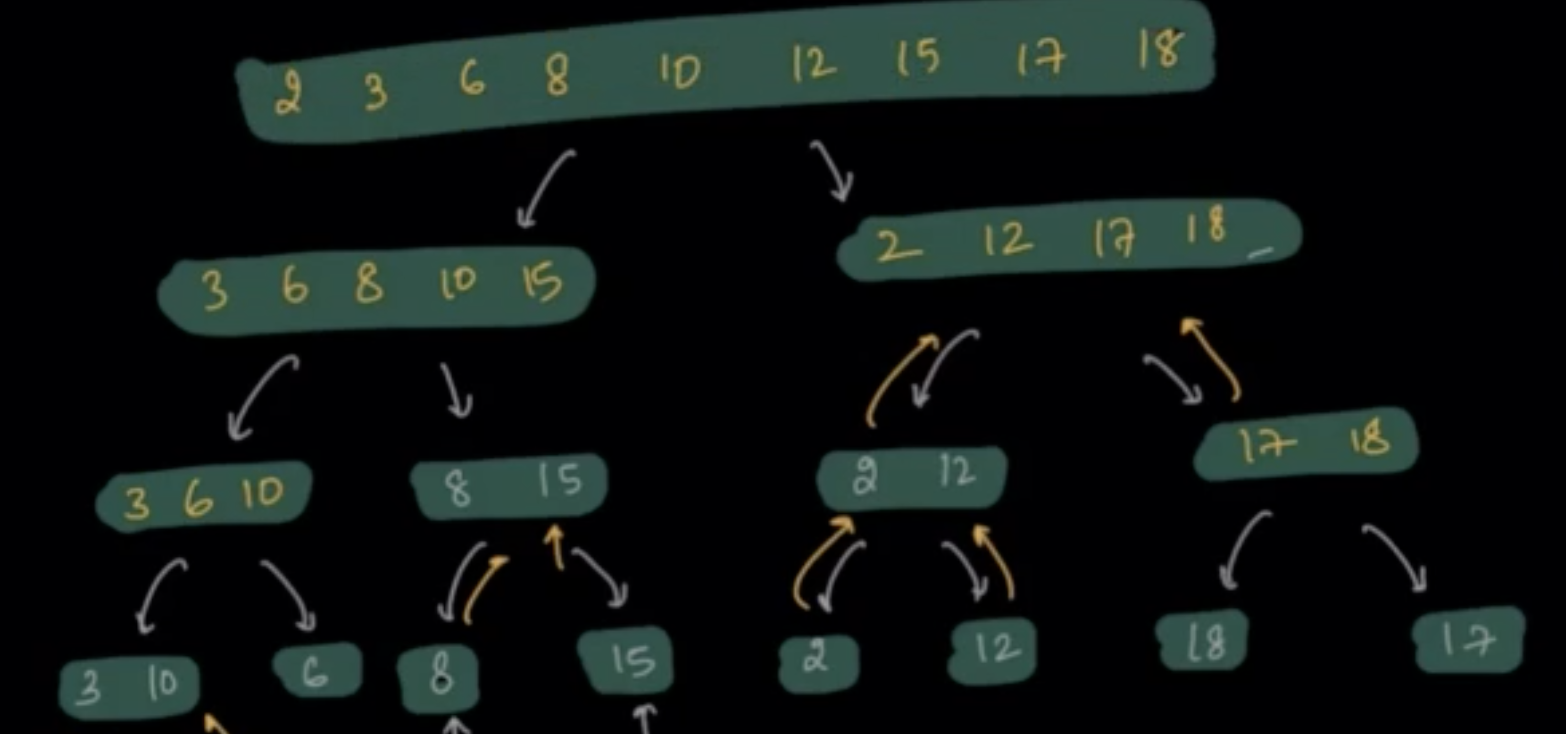
In this way, we have finally sorted the array.

This algorithm of dividing the array into multiple subproblems and merging them one by one is called Merge Sort.

Since we are breaking down the array into multiple subproblems and applying the same idea to merge them, we are using the technique of Recursion.

Psuedocode¶

void merge(A[], l, mid, r) {
  int N = A.length();
  int n1 = mid - l + 1;
  int n2 = r - mid;

  int B[n1], C[n2];

  int idx = 0;
  for (int i = l; i <= mid; i++) {
    B[idx] = A[i];
    idx++;
  }

  idx = 0;
  for (int i = mid + 1; i <= r; i++) {
    C[idx] = A[i];
    idx++;
  }

  idx = l;
  i = 0; // moves over A
  j = 0; // moves over B

  while (i < n1 && j < n2) {
    if (B[i] <= C[j]) {
      A[idx] = B[i];
      i++;
    } else {
      A[idx] = C[j];
      j++;
    }
    idx++;
  }

  while (i < n1) {
    A[idx] = B[i];
    idx++;
    i++;
  }

  while (j < n2) {
    A[idx] = C[j];
    idx++;
    j++;
  }
}

void mergeSort(int A[], l, r) {
  if (l == r) return; // base case

  int mid = (l + r) / 2;
  mergeSort(A, l, mid);
  mergeSort(A, mid + 1, r);
  merge(A, l, mid, r);
}

Complexity Analysis:¶

If we divide the arrays in two halves, we will have a tree structure as:

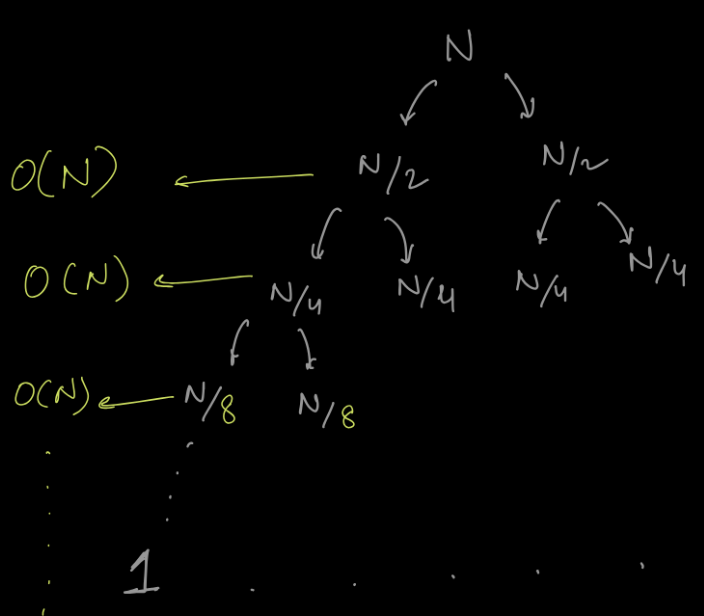
The time taken at every level is the time taken by merging the arrays which will be O(N).

Height of Tree / Number of Levels - O(log N)

Thus, Time Complexity: O(N * log(N))

Space Complexity: O(N)

For recursive stack, we require O(logN) space. And at every level, we are using O(N) space for merging but since we are freeing that as well. We are utilizing O(N) in total merging. Thus, space complexity is O(logN) + O(N) = O(N)

Merge sort is stable as arrangement of elements is taking place at merge step which is essentially maintaining the relative order of elements.

Calculate no of pairs such that A[i] > B[j]¶

Given two array, A[n] and B[m]; Calculate number of pairs i,j such that A[i] > B[j].

Example

A[3] = {7, 3, 5}
B[3] = {2, 0, 6}

Explanation

(7,2) (7,0) (7,6) (3,2) (3,0) (5,2) (5,0) (7 pairs)

Warning

Please take some time to think about the bruteforce approach on your own before reading further.....

Brute Force Approach¶

Take 2 loops and compare the values

TC & SC¶

Time complexity is O(n * m)
Space complexity is O(1)

Appoach 2 with Dry Run¶

Sort both the arrays
Create one array, C[6] for merging both the arrays
Assign pointer P1, P2, P3 to A[0], B[0], C[0] respectively
A[3] = {3, 5, 7} <-- P1
B[3] = {0, 2, 6} <-- P2
B[0] < A[0] means 0 is smaller than every element in A from index 0 onwards; count of pairs = 3 (3,0)(5,0)(7,0); C[] ={0}; P2=1
B[1] < A[0] means 2 is smaller than every element in A from index 0 onwards; count of pairs = 6 (3,0)(5,0)(7,0)(3,2)(5,2)(7,2); C[] ={0, 2}; P2=2
B[2] > A[0] means 6 can't form a pair with 3. We are done with 3, because if 6 can't make a pair, no other element after 6 can make a pair with 3; C[]={0, 2, 3}; P1=1
B[2] > A[1] means 6 can't form a pair with 5. We are done with 5, because if 6 can't make a pair, no other element after 6 can make a pair with 5; C[]={0, 2, 3, 5}; P1=2
B[2] < A[2] means 6 is smaller than every element in A from index 2 onwards; count of pairs = 7(3,0)(5,0)(7,0)(3,2)(5,2)(7,2)(7,6); C[] ={0, 2, 3, 5, 6}; P2=3
B is empty, we can push all elements remaining in A to C; C[] ={0, 2, 3, 5, 6, 7};

Time Complexity¶

O(nlogn + mlogm + m + n)

Here nlogn is the time complexity of sorting A array, mlogm is the time complexity for B array and m+n is the time complexity for merging both the arrays

Inversion Count¶

Given an a[n], calculate no of pairs [i,j] such that ia[j], i and j are index of array.

Given a[5] = {10, 3, 8, 15, 6}

i < j	a[i] > a[j]
i=0, j=1	a[0] > a[1]
i=0, j=2	a[0] > a[2]
i=0, j=4	a[0] > a[4]
i=2, j=4	a[2] > a[4]
i=3, j=4	a[3] > a[4]

Hence from the above table we can conclude that the ans is 5 as it is valid for only 5 pairs.

Question¶

Consider the following array: [5, 2, 6, 1]. Calculate the inversion count for this array.

Choices

1
2
3
4

Question¶

Consider the following array: [5, 3, 1, 4, 2]. Calculate the inversion count for this array.

Choices

0
5
6
7

Inversion Count Brute Force¶

Create all the pairs and check.

Pseudocode¶

for (int i = 0; i < n; i++) {
  for (int j = i + 1; j < n; j++) { // since j is greater than i
    if (a[i] > a[j])
      cnt++
  }
}

TC for the above code is \(O(n^2)\)

This code will give us time limited exceeded error. So, we need to find a better apporach

Optimised Approach¶

IDEA:

We will slipt the array into two equal parts, and keep on splitting the array till only 1 element is left, just like we do in MERGE SORT.

Now, at the time of merging, we can keep counting the pairs.

Basically, it will be same as what we did in previous question. As we merge the arrays, we can keep on calculating the answer.

Pseudocode - Small change to merge function¶

void merge(A[], l, mid, r) {
  inv_count = 0;
  int N = A.length();
  int n1 = mid - l + 1;
  int n2 = r - mid;

  int B[n1], C[n2];

  int idx = 0;
  for (int i = l; i <= mid; i++) {
    B[idx] = A[i];
    idx++;
  }

  idx = 0;
  for (int i = mid + 1; i <= r; i++) {
    C[idx] = A[i];
    idx++;
  }

  idx = l;
  i = 0; // moves over A
  j = 0; // moves over B

  while (i < n1 && j < n2) {
    if (B[i] <= C[j]) {
      A[idx] = B[i];
      i++;
    } else {
      A[idx] = C[j];
      j++;

      //**ONLY CHANGE IS THE BELOW LINE**

      //Here, we found element on right subarray to be smaller than an element on left, 
      //so we will count all the elements on left [i m-1] = m - i 
      inv_count = inv_count + (m - i);
    }
    idx++;
  }

  while (i < n1) {
    A[idx] = B[i];
    idx++;
    i++;
  }

  while (j < n2) {
    A[idx] = C[j];
    idx++;
    j++;
  }
}

Stable Sort & Inplace¶

Stable Sort¶

Definition:¶

Relative order of equal elements should not change while sorting w.r.t a parameter.

Examples

A[ ] = {6, 5, 3, 5}
After Sorting
A[ ] = {3, 5, 5, 6}

In this case, which 5 comes first, which later, doesn't matter since it is just a singular data.

But in actually scenario the objects to be sorted is collection of data.

Scenario: Let's talk about an Airport checkin line!

It should be First Come first serve, whoever comes first should be allowed first to checkin.

But according to airline, all the members are not same. Some would be economic, business class, priveledged/ priorty...

Say Anand(economic class) is standing and Amir(economic class) comes and tries to move ahead Anand, will Anand be okay with it? Not Really!

Say Anupriya(Business Class), now Anand would be okay!

The above example explains why stable sorting is important.

Another Example:

Name	Marks
A	8
B	5
C	8
D	4
E	8

Sort acc to marks. In which case, if this is stable sort, A,C,E should appear in the same order.

After Sorting

Name	Marks
D	4
B	5
A	8
C	8
E	8

Inplace¶

No extra space
Space complexity: O(1)