Trees 1: Structure & Traversal¶

What is a tree¶

Till now, we have seen data structures such as Arrays, Linked Lists, Stacks, Queues. They are Linear Data Structure which means we can access them in sequencial order.

The other category is Non Linear Data Structure

At a lot of places, you must have seen hierarchy - Family, Office, Computer File System, etc. Therefore, there arise a need to be able to store such type of data and process it.

Tree is an example of a non/linear or hierarchical data structure.

Example¶

Let us see the hierachy of people in an organization:

CEO (Chief Executive Officer)
├── CTO (Chief Technology Officer)
│   ├── Engineering Manager
│   │   ├── Software Development Team Lead
│   │   │   ├── Software Engineer
│   │   │   └── Software Engineer
│   │   └── QA Team Lead
│   │       ├── QA Engineer
│   │       └── QA Engineer
│   └── IT Manager
│       ├── IT Specialist
│       └── IT Specialist
├── CFO (Chief Financial Officer)
│   ├── Finance Manager
│   │   ├── Accountant
│   │   └── Accountant
│   └── Procurement Manager
│       ├── Procurement Officer
│       └── Procurement Officer
└── CMO (Chief Marketing Officer)
    ├── Marketing Manager
    │   ├── Marketing Specialist
    │   └── Marketing Specialist
    └── Sales Manager
        ├── Sales Representative
        └── Sales Representative

As we know that every tree has roots which are below the leaves but in the computer science the case is different the roots are at the top and leaves below it.

Tree naming¶

Example

         1
       /   \
      2     3
     / \   / \
    4   5 6   7
             /
            8

Node: An element in a tree that contains data and may have child nodes connected to it. 1, 2, 3, 4, 5, 6, 7, 8.

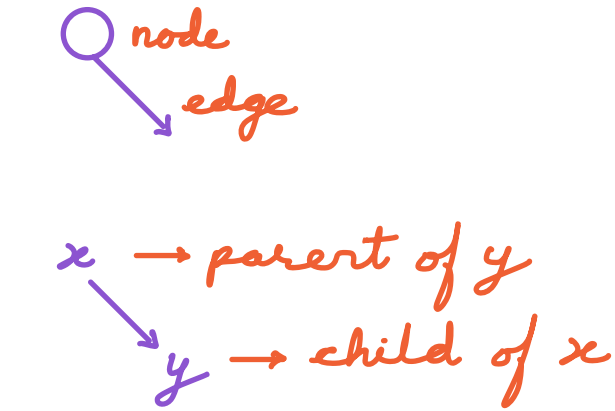
Root:
The topmost node in a tree from which all other nodes descend. It has no parent. Node 1 is the root.
Parent:
A node that has child nodes connected to it. Nodes 1, 2, 3 and 7..
Child:
A node that has a parent node connected to it. Nodes 2, 3, 4, 5, 6, and 7 are children.
Leaf:
A node that has no child nodes. It's a terminal node. Nodes 4, 5, 6, and 8 are leaves.
Depth:
The level at which a node resides in the tree. The root is at depth 0. Depth of node 1 is 0, 2 and 3 are at depth 1, 4, 5, 6, and 7 are at depth 2, and 8 is at depth 3.
Height:
The length of the longest path from a node to a leaf. The height of the tree is the height of the root node. Height of the tree is 3, which is the number of edges from the root to a farthest leaf (8).
Subtree:
A tree structure that is part of a larger tree. Subtree rooted at node 2 consists of nodes 2, 4, and 5.
Siblings:
Nodes that share the same parent node. Nodes 2 and 3 are siblings.
Ancestor:
All nodes from parent to the root node upwards are the ancestors of a node. Nodes 1, 3, 7 are ancestors of node 8.
Descendant:
All nodes from child to the leaf node along that path. Nodes 4 and 5 are descendants of node 2.

Question¶

Can a leaf node also be a subtree?

Choices

YES
NO
Can't say

Explanation:

Yes, a leaf node can also be considered a subtree. A subtree is a portion of a tree structure that is itself a tree.

Question¶

Do all nodes have a parent node?

Choices

YES
NO
Can't say

Explanation:

In a tree data structure, all nodes except for the root node have a parent node.

Levels of a tree¶

    1            Level 0
   / \
  2   3          Level 1
 / \
4   5            Level 2

In this example:

Level 0: Node 1 is at level 0 (root level).
Level 1: Nodes 2 and 3 are at level 1.
Level 2: Nodes 4 and 5 are at level 2.

Question¶

What is the height of the leaf node in any tree?

Choices

0
1
2
3

Explanation

The height of a leaf node in any tree, including a binary tree, is 0. This is because the height of a node is defined as the length of the longest path from that node to a leaf node, and a leaf node is a node that doesn't have any children. Since there are no edges to traverse from a leaf node to a leaf node, the length of the path is 0.

Binary Tree¶

A type of tree in which each node can have at most two children i.e, either 0, 1 or 2, referred to as the left child and the right child.

Example of a binary tree:

         10
       /    \
      5     15
     / \    / \
    3   8  12  18

Traversals in a Tree¶

How can we traverse a Tree ?¶

There are many ways to traverse the tree.

L: Left Subtree, R: Right Subtree, N: Root Node

L N R	L R N	R N L
R L N	N L R	N R L

Having so many traversals can be confusing and are unnecessary. Threfore, a standard has been set where first we'll always consider the Left Subtree and then the Right Subtree. Therefore, we boil down to 3 traverals.

L N R	Named as Inorder
N L R	Named as Preorder
L R N	Named as Postorder

Names are given w.r.t the position of the root node.

There are more techniques for traversing a tree that'll be covered in next set of sessions.

Pre-order¶

Pre-order traversal is a depth-first traversal technique used to visit all nodes of a binary tree in a specific order. In pre-order traversal, you start from the root node and follow these steps for each node:

Visit the current node.
Traverse the left subtree (recursively).
Traverse the right subtree (recursively).

This traversal order ensures that the root node is visited before its children and the left subtree is explored before the right subtree.

Example:

         10
       /    \
      5     15
     / \    / \
    3   8  12  18

Pre-order traversal sequence: 10, 5, 3, 8, 15, 12, 18

Pseudocode¶

void preorder(root) {
    if (root == null)
        return;

    print(root.data); //node
    preorder(root.left); //left
    preorder(root.right) //right
}

In-order traversal¶

In-order traversal is another depth-first traversal technique used to visit all nodes of a binary tree, but in a specific order. In in-order traversal, you follow these steps for each node:

Traverse the left subtree (recursively).
Visit the current node.
Traverse the right subtree (recursively).

This traversal order ensures that nodes are visited in ascending order if the binary tree represents a search tree.

Here's an example of in-order traversal on a binary tree:

         10
       /    \
      5     15
     / \    / \
    3   8  12  18

In-order traversal sequence: 3, 5, 8, 10, 12, 15, 18

Pseudocode¶

void inorder(root) {
    if (root == null)
        return;

    inorder(root.left); //left
    print(root.data); //node
    inorder(root.right) //right
}

Post-order Traversal¶

Post-order traversal is another depth-first traversal technique used to visit all nodes of a binary tree, but in a specific order. In post-order traversal, you follow these steps for each node:

Traverse the left subtree (recursively).
Traverse the right subtree (recursively).
Visit the current node.

This traversal order ensures that nodes are visited from the bottom up, starting from the leaf nodes and moving towards the root node.

Example

         10
       /    \
      5     15
     / \    / \
    3   8  12  18

Post-order traversal sequence: 3, 8, 5, 12, 18, 15, 10

Pseudocode:¶

void postorder(root) {
    if (root = null) return;
    postorder(root.left) left
    postorder(root.right) right
    print(root.data) Node
}

Question¶

What is the inorder traversal sequence of the below tree?

         1
       /    \
      2      4
     /      / \
    3      5   6

Choices

[1, 2, 3, 4, 5, 6]
[3, 2, 1, 5, 4, 6]
[3, 2, 1, 4, 5, 6]
[4, 5, 6, 1, 2, 3]

Explanation

The inorder traversal sequence is [3, 2, 1, 5, 4, 6].

Iterative Inorder traversal¶

Approach:¶

Iterative Inorder traversal is a method to visit all the nodes in a binary tree in a specific order without using recursion.
In the case of Inorder traversal, you visit the nodes in the following order: left subtree, current node, right subtree.
Here's how you can perform an iterative Inorder traversal using a stack data structure, along with an example:

Let's say we have the following binary tree as an example:

Dry-Run:¶

Start at the root node (1).
Push 1 onto the stack and move left to node 2.
Push 2 onto the stack and move left to node 4.
Push 4 onto the stack and move left; there are no left children, so pop 4, visit it, and move right (which is null).
Pop 2, visit it, and move to its right child, node 5.
Push 5 onto the stack and move left; there are no left children, so pop 5, visit it, and move right (which is null).
Pop 1, visit it, and move to its right child, node 3.
Push 3 onto the stack and move left; there are no left children, so pop 3, visit it, and move right (which is null).
The stack is empty, and all nodes have been visited.
So, the iterative Inorder traversal of the tree is 4, 2, 5, 1, 3.

Need of recursion/stack:¶

In inorder traversal of a binary tree, you need a data structure like a stack or recursion because you need to keep track of the order in which you visit the nodes of the tree. The reason for using these techniques is to handle the backtracking that's inherent in traversing a binary tree in inorder fashion. In a binary tree's inorder traversal, you visit nodes in a specific order: left, current, right. You use a stack or recursion to remember where you left off in the tree when moving between nodes, ensuring you visit nodes in the correct order and navigate through the tree efficiently. This backtracking is essential for proper traversal.

Pseudocode:¶

cur = root;
while (cur != null || st.isempty()) {
    if (cur != null) {
        st.push(curr)
        cur = cur.left;
    } else {
        cur = st.pop();
        print(cur.data)
        cur = cur.right
    }
}

Complexity¶

Time Complexity: O(N)

Space Complexity: O(N)

Construct binary tree from inorder and post order¶

Constructing a binary tree from its inorder and postorder traversals involves a recursive process. Here's a brief explanation with an example:

Brute-Force Approach¶

Generate all possible permutations of the given inorder traversal.
For each permutation, check if it forms a valid binary tree when combined with the given postorder traversal.
Return the first valid binary tree found.

Example:

Inorder: [4, 2, 7, 5, 1, 3, 6] Postorder: [4, 7, 5, 2, 6, 3, 1]

Dry-Run:¶

Identify the root: In the postorder traversal, the last element is 1, which is the root of the binary tree.
Split into left and right subtrees: In the inorder traversal, find the position of the root element (1). Elements to the left of this position represent the left subtree, and elements to the right represent the right subtree.
Recurse on left subtree: For the left subtree, the root is 2 (found in postorder traversal). Split the left subtree's inorder and postorder traversals, and repeat the process.
Recurse on right subtree: For the right subtree, the root is 3 (found in postorder traversal). Split the right subtree's inorder and postorder traversals, and repeat the process.
Continue the recursion: Repeat steps 3 and 4 for each subtree until the entire binary tree is constructed.

Pseudocode:¶

function buildTreeBruteForce(inorder, postorder):
    for each permutation of inorder:
        if formsValidBinaryTree(permutation, postorder):
            return constructBinaryTree(permutation, postorder)
    return null

Complexity¶

Time Complexity: O(N! * N)

Space Complexity: O(N)

Warning

Please take some time to think about the optimised approach on your own before reading further.....

Most-Optimised Approach:¶

The last element in the postorder traversal is the root of the binary tree.
Find the root element in the inorder traversal to determine the left and right subtrees.
Recursively repeat the process for the left and right subtrees.

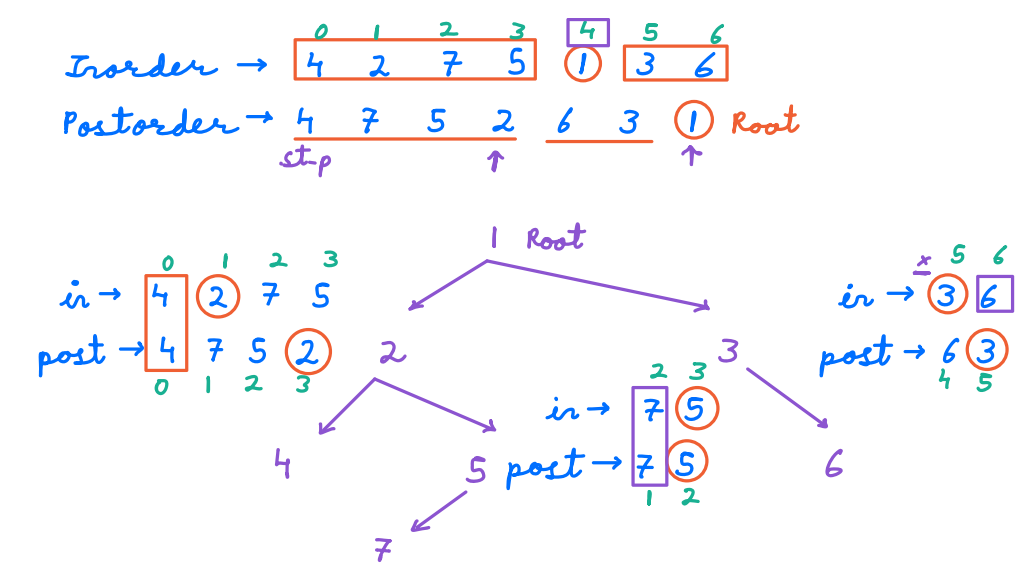
Now as we can see in the above image let us understand this with the help of a dry/run:

Dry-Run/Example:¶

inorder={4,2,7,5,1,3,6} and postorder={4,7,5,2,6,3,1}

The last element in the postorder traversal is 1, which is the root of the binary tree.

Binary Tree:

Find 1 in the inorder traversal to split it into left and right subtrees. The elements to the left are the left subtree, and the elements to the right are the right subtree.

Inorder: [4,2,7,5,1,3,6]
Postorder: [4,7,5,2,6,3,1]

Left Subtree (Inorder: [4,2,7,5], Postorder: [4,7,5,2]):

Right Subtree (Inorder: [3,6], Postorder: [6,3]):

6
 \
  3

Repeat the process for the left and right subtrees:

For the left subtree:

The last element in the postorder traversal is 2, which is the root of the left subtree.
Find 2 in the inorder traversal to split it into left and right subtrees.
Left Subtree (Inorder: [4], Postorder: [4]):

  2
 /
4

Right Subtree (Inorder: [7,5], Postorder: [7,5]):

  5
 /
7

For the right subtree:

The last element in the postorder traversal is 3, which is the root of the right subtree.
Find 3 in the inorder traversal to split it into left and right subtrees.
Left Subtree (Inorder: [6], Postorder: [6]):

  3
   \
    6

The final binary tree would look like this:

Question¶

The inorder traversal sequence [4, 2, 5, 1, 6, 3] and the postorder traversal sequence [4, 5, 2, 6, 3, 1]. What is the root of the binary tree?

Choices

1
2
3
4

Explanation:

In postorder traversal, the last element is always the root of the tree, so here, 1 is the root.

Construct binary tree Pseudocode¶

Pseudocode:¶

rootIndex is the index of the root value in the inorder array.
rootIndex + 1 represents the start of the right subtree in the arrays.
end represents the end of the right subtree in the arrays.
start represents the start of the left subtree in the arrays.
rootIndex - 1 represents the end of the left subtree in the arrays.

function buildTree(inorder, postorder):
    if postorder is empty:
        return null

    // The last element in postorder is the root of the current subtree
    rootValue = postorder.last
    root = new TreeNode(rootValue)

    // Find the index of the rootValue in inorder to split it into left and right subtrees
    rootIndex = indexOf(inorder, rootValue)

    // Recursive call for right subtree
    root.right = buildTree(subarray(inorder, rootIndex + 1, end), subarray(postorder, rootIndex, end - 1))

    // Recursive call for left subtree
    root.left = buildTree(subarray(inorder, start, rootIndex - 1), subarray(postorder, start, rootIndex - 1))

    return root

Complexity¶

Time Complexity: O(N)

Space Complexity: O(N)