Advanced DSA : Arrays 2: Two Dimensional¶

Problem 1 Find in rowise and colwise sorted matrix¶

Problem Statement¶

Given a row wise and column wise sorted matrix, find out whether element k is present or not.

Example

Observe that rows and columns are both sorted.

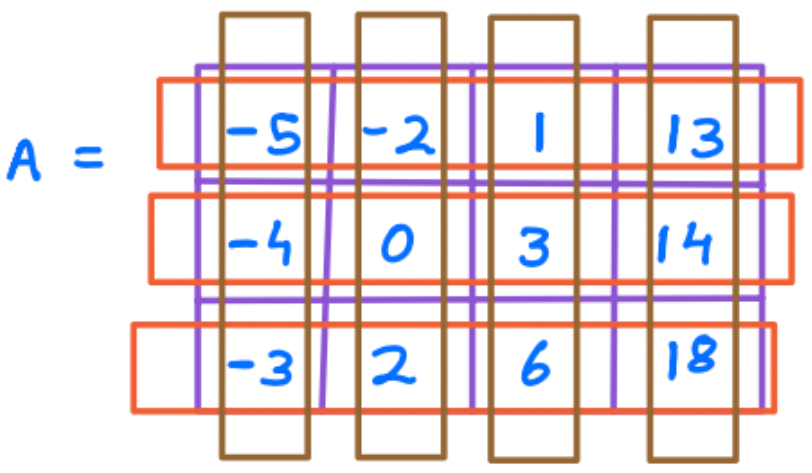
Test Case 1

13 => Present (true)

Test Case 2

2 => Present (true)

Test Case 3

15 => Not Present (false)

Question¶

What is the brute force approach and the time complexity of it?

Choices

Iterate over first row; T.C - O(M)
Iterate over last col; T.C - O(N)
Iterate over all rows & cols; T.C - O(N * M)
Iterate over first col; T.C - O(N)

Warning

Please take some time to think about the solution approach on your own before reading further.....

Idea¶

We shall exploit the property of the matrix being sorted.
Start with the cell from where we can decide the next step.

Example:

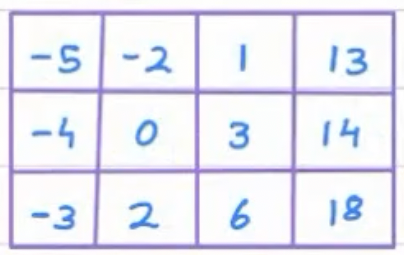
Search for: 0

Say we stand at top left cell i.e, -5.
Now, -5 < 0, can we determined the direction to search based on this?
No, because on rightside as well as downwards, the elements are in increasing order, so 0 can be present anywhere.

Now, say we stand at top right cell i.e, 13.
Now,13 > 0, should we go left or down ? Can we decide ?
Yes, if we move down the elements are > 13, but we are looking for an element < 13, so we should move left.

It means, all elements below 13, can be neglected.

Move Left

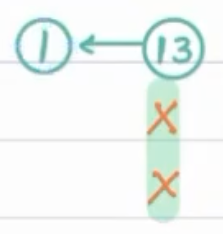
Now, where shall we move ?

Question¶

Say we are at 1 and want to find 0, where should we move ?

Choices

left
bottom
let's move in both the directions
let's move everywhere

Find in rowise and colwise sorted matrix Optimised Approach Continued¶

Since, 1 > 0, again all elements below 1 are greater than 1, hence can be neglected.

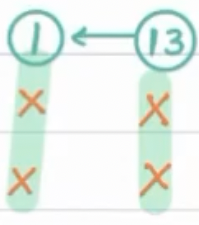
Move Left

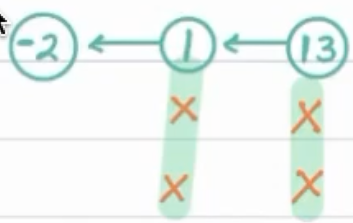
Now, -2 < 0, all elements on left of -2 are lesser than -2, hence can be neglected.

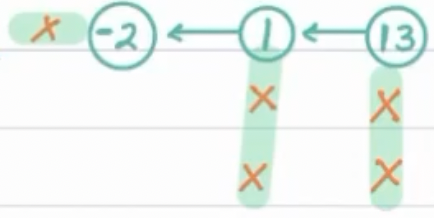
Move Down

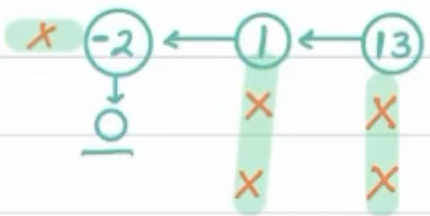
Approach¶

We can start at top right cell.
If A[i][j] < K, move down, else move left.
Repeat until the element is found, our the search space is exhausted.

NOTE: We could have also started at bottom left cell.

Pseudocode¶

int i = 0, j = M - 1
while (i < N && j >= 0) {
  if (arr[i][j] == K) {
    return true;
  } else if (arr[i][j] < K) {
    i++; //move down; next row
  } else {
    j--; //move left; previous column
  }
}
return false;

Time & Space Complexity¶

Time Complexity: O(M+N)

since at every step, we are either discarding a row or a column. Since total rows+columns are N+M, hence Iterations will be N+M.

Space Complexity: O(1)

Problem 2 Row with maximum number of 1s¶

Given a binary sorted matrix A of size N x N. Find the row with the maximum number of 1.

NOTE:

If two rows have the maximum number of 1 then return the row which has a lower index.
Assume each row to be sorted by values.

Example 1:

Output 1: 0^th row

Example 2:

Output 2: 3th row

Warning

Please take some time to think about the solution approach on your own before reading further.....

Brute Force¶

We can iterate over each row and maintain the max number of 1s.

Complexity¶

Time Complexity: O(N * N)

Question¶

Find the row with the maximum number of 1.
Note : If there are two rows with same no. of 1, consider the smaller row.

0	1	1	1
0	0	0	1
1	1	1	1
1	1	1	1

Choices

0^th Row
1^st Row
2^nd Row
3^rd Row

Optimisation Approach¶

We know that rows are sorted, how can we utilise this property of the matrix ?

Idea¶

Say we start from top right of first row and saw that there are 2 ones. Now, in the next row, we don't want to see 2 1s, rather we'll check if 3^rd 1 is present or not?

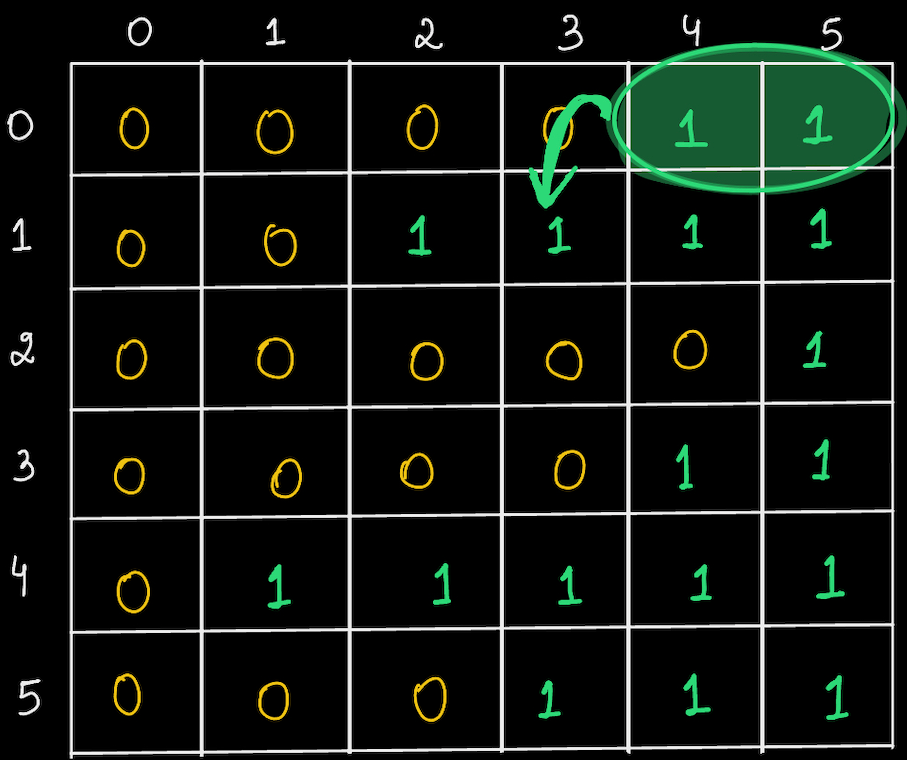
If yes, it means we have three 1s, but then we want to check if more 1s are there, so we'll move towards left in the same row and check.

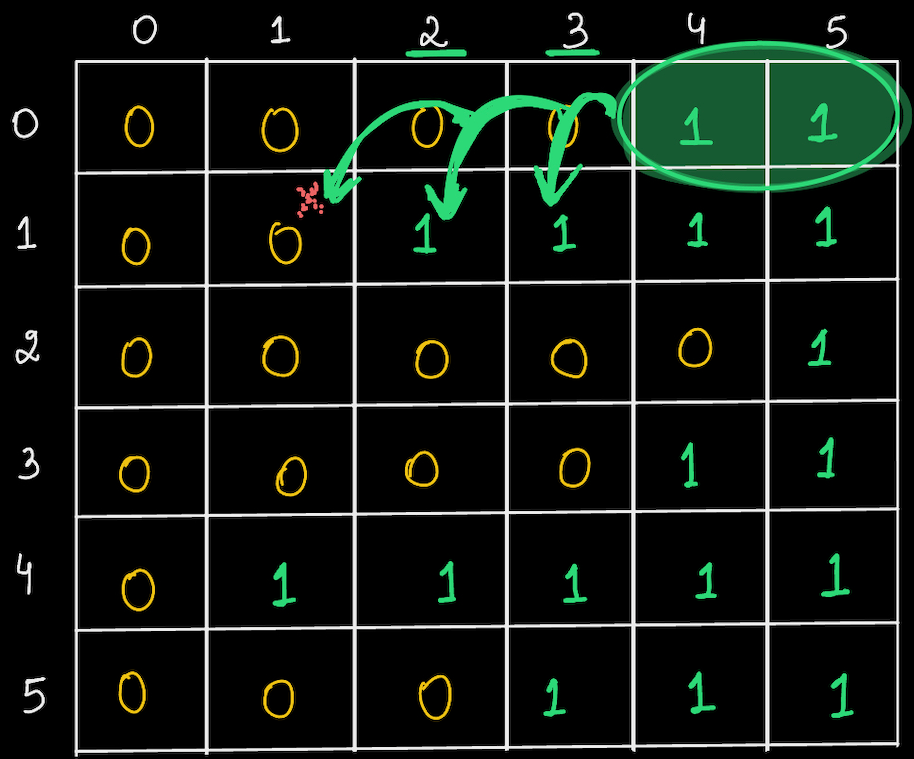
Now, in the subsequent rows, we'll proceed in the same manner.

In 2^nd and 3^rd rows, 1 is not present at 1^st index.

In 4^th row, it is present. So, we check on left if more 1s are present.

In 4^th row, we found the maximum 1s, i.e 5 in total. Hence that is our answer.

Algorithm¶

Start at i = 0, j = M - 1
If 1 is present, decrement j i.e, move towards the left column.
- Whenever j is decremented, it means that row has more 1s, so we can update our answer to that particular row number
If 0 is present, then we want to check in next row that if 1 is present, so we increment i

Pseudocode¶

i = 0, j = N - 1

while (i < N && j >= 0) {
  while (j >= 0 && arr[i][j] == 1) {
    j--;
    ans = i;
  }
  i++;
}
return ans;

Complexity¶

Time Complexity: O(M + N)

since at every step, we are either discarding a row or a column. Since total rows+columns are N+M, hence Iterations will be N+M.

Space Complexity: O(1)

Problem 3 Print Boundary Elements¶

Given an matrix of N X N i.e. Mat[N][N], print boundary elements in clockwise direction.

Example:

N = 5

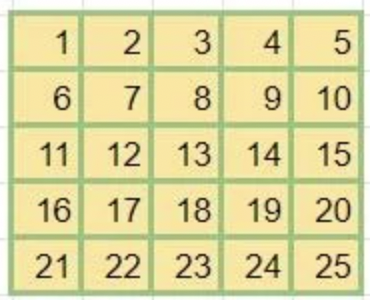
Output:

[1, 2, 3, 4, 5, 10, 15, 20, 25, 24, 23, 22, 21, 16, 11, 6]

Question¶

Given N and matrix mat, select the correct order of boundary elements traversed in clockwise direction.

N = 3

mat :-

1	2	3
4	5	6
7	8	9

Choices

[1, 2, 3, 6, 9, 8, 7, 4]
[1, 4, 7, 8, 9, 6, 3, 2]
[1, 2, 3, 4, 5, 6, 7, 8]
[2, 3, 4, 5, 6, 7, 8, 9]

Warning

Please take some time to think about the solution approach on your own before reading further.....

Approach¶

Print N - 1 elements of first row from left to right
Print N - 1 elements of last column from top to bottom
Print N - 1 elements of last row from right to left
Print N - 1 elements of first column from bottom to top

Pseudocode¶

function printBoundaryElements(Mat[][], N) {
  i = 0 j = 0

  // Print  N - 1  elements of first row from left to right

  for (idx = 1; idx < N; idx++) {
    print(Mat[i][j] + ",")
    j++
  }

  // Print  N - 1  elements of last column from top to bottom
  // i and j will already be 0 and 4 respectively after above loop ends

  for (idx = 1; idx < N; idx++) {
    print(Mat[i][j] + ",")
    i++
  }

  // Print  N - 1  elements of last row  from right to left
  // i and j will already be 4 and 4 respectively after above loop ends

  for (idx = 1; idx < N; idx++) {
    print(Mat[i][j] + ",")
    j--
  }

  // Print  N - 1  elements of first column from bottom to top
  // i and j will already be 4 and 0 respectively after above loop ends

  for (idx = 1; idx < N; idx++) {
    print(Mat[i][j] + ",")
    i--
  }
}

Complexity¶

Time Complexity : O(N)
Space Complexity : O(1)

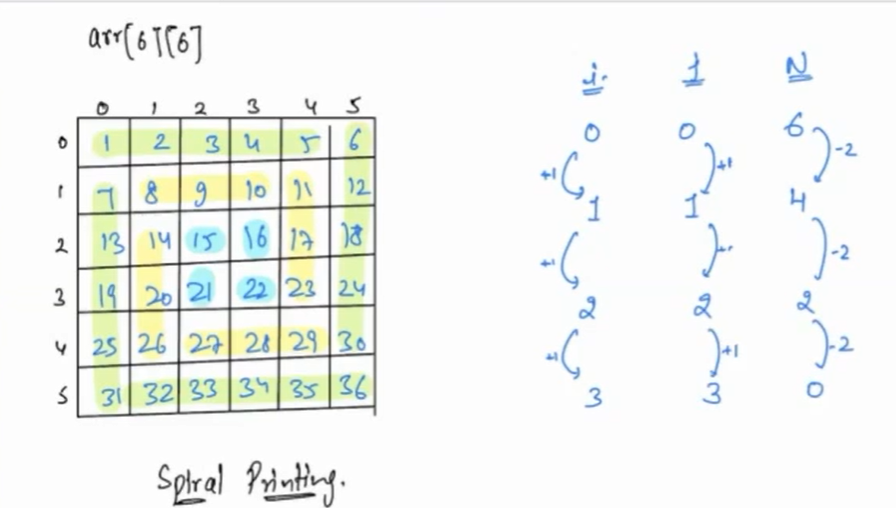
Problem 4 Spiral Matrix¶

Given an matrix of N X N i.e. Mat[N][N]. Print elements in spiral order in clockwise direction.

Example

N = 5

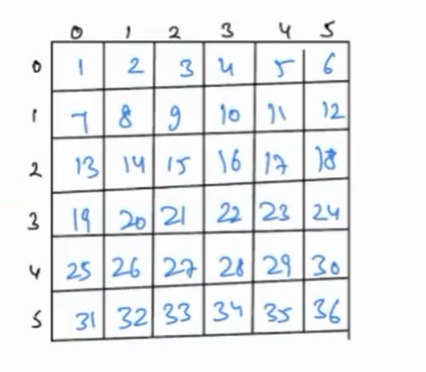
Here is the depiction to understand the problem better

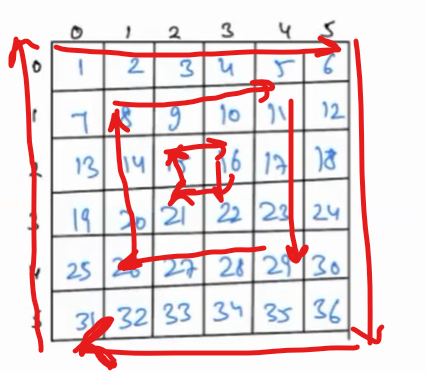
Solution = [1,2,3,4,5,6,12,18,24,30,36,35,34,33,32,31,25,19,13,7,8,9,10,11,17,23,29,28,27,26,20,14,15,16,22,21]

The red arrow represents direction of traversal(clockwise) and fashion in which elements are traversed.

Warning

Please take some time to think about the solution approach on your own before reading further.....

Approach¶

We can break the problem into several boundary printing problem discussed above
So first print boundary of matrix of N x N
Then we print boundary of next submatrix with top left element being (1,1) and Bottom right element being (N - 2 , N - 2).
After every boundary, to print the next boundary, N will be reduced by 2 and i & j will be incremented by 1.
We do this till matrix of size least size is reached.

Boundaries of submatricies are highlighted in different color.

Edge Case¶

Will the above code work if matrix size is 1 ?
No, since the loops run N-1 times, therefore we have to handle it separately.

Question¶

Print elements in spiral order in clockwise direction.

13	14	12	8
9	1	2	7
0	4	3	0
10	5	6	11

Choices

[13, 9, 0, 10, 5, 6, 11, 0, 7, 8, 12, 14, 1, 4, 2, 3]
[13, 14, 12, 8, 9, 1, 2, 7, 0, 4, 3, 0, 10, 5, 6, 11]
[13, 14, 12, 8, 7, 0, 11, 6, 5, 10, 0, 9, 1, 2, 3, 4]
[13, 14, 12, 8, 10, 5, 6, 11, 9, 1, 2, 7, 0, 4, 3, 0]

Pseudocode¶

Function printBoundaryElements(Mat[][], N) {
  i = 0 j = 0
  while (N > 1) {

    // Print  N-1  elements of first row from left to right
    for (idx = 1; idx < N; idx++) {
      print(Mat[i][j] + ",")
      j++
    }

    // Print  N-1  elements of last column from top to bottom
    for (idx = 1; idx < N; idx++) {
      print(Mat[i][j] + ",")
      i++
    }

    // Print  N-1  elements of last row  from right to left
    for (idx = 1; idx < N; idx++) {
      print(Mat[i][j] + ",")
      j--
    }

    // Print  N-1  elements of first column from bottom to top
    for (idx = 1; idx < N; idx++) {
      print(Mat[i][j] + ",")
      i--
    }

    N = N - 2
    i++
    j++
  }

  if (N == 1) {
    print(Mat[i][j] + ",")
  }
}

Complexity¶

Time Complexity : O(N^2)
Space Complexity : O(1)

What is a submatrices and how can we uniquely identify it¶

What is a submatrix?¶

Same as how a subarray is continuous part of an Array, a submatrix is continuous sub-matrix of a matrix.

Example,

11	12
15	16

is submatrix of the below matrix.

How can we uniquely indentify a rectangle ?¶

A rectangle is made up of 4 coordinates.

Top Left (TL)
Top Right (TR)
Bottom Left (BL)
Bottom Right (BR)

If we pick any two diagonal coordinates, we can uniquely identify a rectangle.

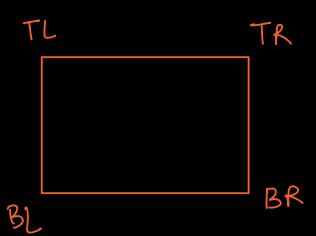
So, let's say we pick TL and BR.

Example -

If TL = (3,2) and BR = (2,3)
Then we know which rectangle we are talking about(shown below).

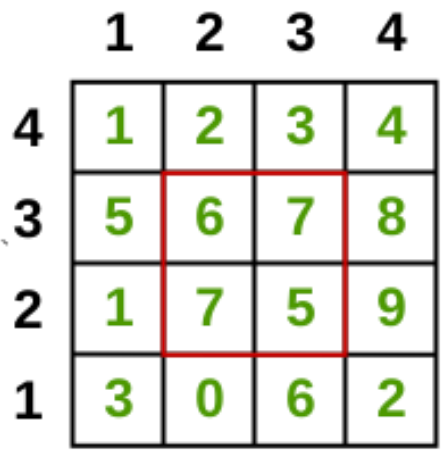
So, with the help of TL and BR coordinates(or TR & BL), we can uniquely identify a submatrices.

Problem 5 Sum of all Submatrices Sum¶

Given a matrix of N rows and M columns determine the sum of all the possible submatrices.

Example:

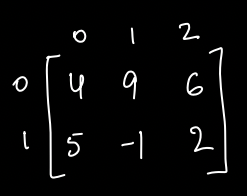
All Possible sub-matrices are -

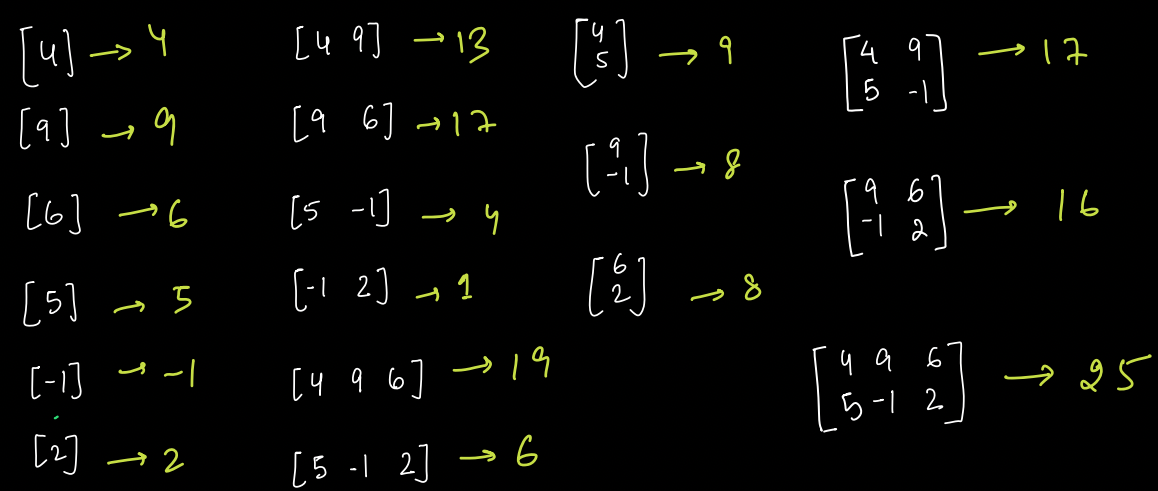
Total Sum = 166

Warning

Please take some time to think about the solution approach on your own before reading further.....

Approach¶

This question sounds same as "Sum of all Subarray Sums". We did that question is Intermediate - Subarrays. The technique used was Contribution Technique, where for every element we had to find that in how many subarrays it was part of.

In "Sum of all Submatrices Sums", we have to find that in how many submatrices a particular element is part of.

If we are able to find that, then we just have to add up the individual results.

In what all submatrices, a particular element is part of ?¶

Let's look at the red cell in below figure.
If we combine all the top left cells(marked with green color) with all the bottom right cells(marked with blue color), then in all those submatrices, the red cell will be present.

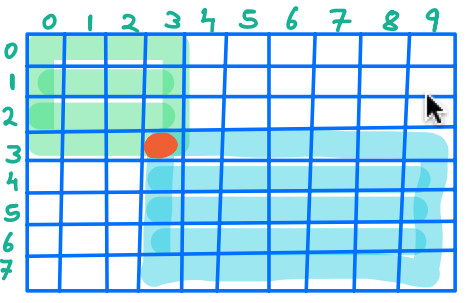
How to find the number of TL cells and BR cells in which (i,j) is part of.¶

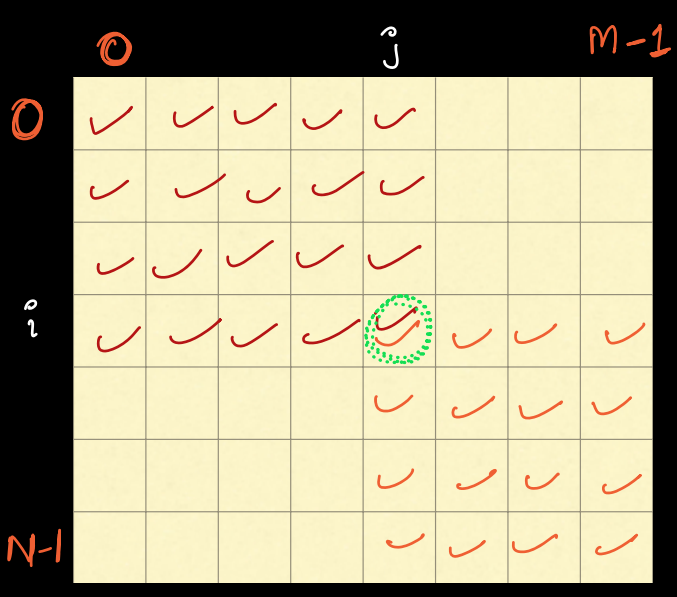
TOP LEFT:

rows: [0 i]
cols: [0 j]
total cells = (i+1) * (j+1)

BOTTOM RIGHT:

rows: [i N-1]
cols: [j M-1]
total cells = (N-i) * (M-j)

Now, to find the total submatrices of whish (i,j) is part of -¶

contribution of (i,j) = TOP LEFT * BOTTOM RIGHT

Every top left cell can be combined with every bottom right cell.

Example

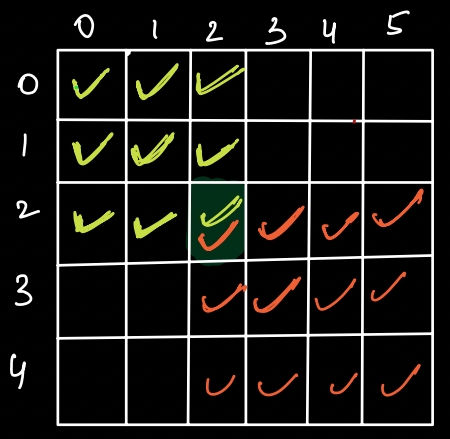
For (2,2)

TOP LEFT:
3 * 3 = 9

BOTTOM RIGHT
(5-2) * (6-2) = 3 * 4 = 12

Total matrices of which (2,2) is part of 9 * 12.

Question¶

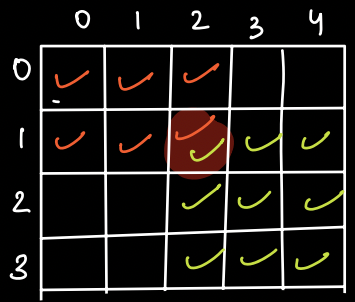
In a matrix of size 4 * 5, in how many submatrices (1,2) is part of ?

Choices

56
54
15
16

Pseudocode¶

total = 0
for (int i = 0; i < N; i++) {
  for (int j = 0; j < M; j++) {

    top_left = (i + 1) * (j + 1);
    bottom_right = (N - i) * (M - j);

    contribution = A[i][j] * top_left * bottom_right;

    total += contribution
  }
}
return total