Two Pointers

---

Problem 1 Pairs with given sum 2

Given an integer sorted array A and an integer k, find any pair (i, j) such that A[i] + A[j] = k, i != j.

Example: A = [-5, -2, 1, 8, 10, 12, 15]
k = 11

Ans: (2, 4) as A[2] + A[4] = 1 + 10 = 11 = k

---

Question

Check if there exists a pair with sum k A [ ] = { -3, 0, 1, 3, 6, 8, 11, 14, 18, 25 } k = 12

Choices

• Yes
• No

Explanation:

Yes. Because there are 2 pairs with sum as 11, They are

• (1, 11)
• (3, 8)

---

Warning

Please take some time to think about the solution approach on your own before reading further.....

Pairs with given sum 2 Approaches

Brute Force Apporach:

Run two for loops and for every indices: i, j, check if sum is k.

• Time Complexity:

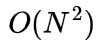, as we need to use two for loops.

• Space Complexity: O(1), as no additional space is required.

Binary Search Apporach

Observation:

• We need to find two elements whose sum is k, i.e., A[i] + A[j] == k.
• So, A[j] = k - A[i]. Essentially, for an element, A[i], we need to find an element k - A[i].
• Since, array A is sorted, we can use binary search to find the element k - A[i]. (make sure, we are not choosing the same index again)

Approach: For all i, binary search and find k - A[i].

• Time Complexity: O(N * log(N)), as we need to apply binary search for every element in the worst case.

• Space Complexity: O(1), as no additional space is required.

---

Pairs with given sum 2 Two Pointers Approach

Let's keep two pointers, i and j and we put them at 0 and 1^st idx.

We have, A = {-5, -2, 1, 8, 10, 12, 15} and k = 11

If A[0] = A[i] = -5 and A[1] = A[j] = -2
A[i] + A[j] = -5 + (-2) = -7
So, A[i] + A[j] < k

To achieve the sum as k, we have to either increase i or j as the array is sorted.

Now, if A[5] = A[i] = 12 and A[6] = A[j] = 15
A[i] + A[j] = 12 + 15 = 27
So, A[i] + A[j] > k

In this case, to achieve k, we have to either decrease i or j. Why?

Essentially, we want to decrease the sum. The sum can be decreased by decreasing A[i] or A[j]. Since array is sorted, decrease the pointers will decrease the value as well.

Where should we place the pointers initially?

Initially, the pointers should be place at the beginning and end of the array as this way, we will have only one pointer in option to move in order to increase / decrease the sum.

Step 1:

So, if we take A[i] = A[0] and A[j] = A[6] then,
A[i] + A[j] = A[0] + A[6] = -5 + 15 = 10 < k. So, we need to increase the sum. Which pointer should we move?

Observations:

• This implies -5 + largest element is less than k. Therefore, -5 + any element of A will always be less than k. So, we do not need to check -5 with any other number as the array is sorted.
• Hence, we should increase the i pointer to increase the sum.

Note: Our motive here is to eliminate the elements one by one till we reach towards the elements who can build the required sum. Since, -5 + largset element < k, we can safely eliminate -5.

Step 2:

Now, taking A[i] = A[1] = -2 and A[j] = A[6] = 15
A[i] + A[j] = -2 + 15 = 13
Here, A[i] + A[j] > k
Following the same approach, we should decrease the index of j to decrease the sum. As decreasing the i would take us to the Step 1.

Step 3:

Now, taking A[i] = A[1] = -2 and A[j] = A[5] = 12
A[i] + A[j] = -2 + 12 = 10
Here A[i] + A[j] < k
Following the same approach, we should increase the index of i to increase the sum.

Step 4:

Similary, taking A[i] = A[2] = 1 and A[j] = A[5] = 10
A[i] + A[j] = 1 + 10
Here, A[i] + A[j] = k.

Pseudocode:

while (i < j) {
  if (A[i] + A[j] == k) {
    return (i, j);
  } else if (A[i] + A[j] < k) {
    i++;
  } else {
    j--;
  }
}

• Time Complexity: O(N), as we need to traverse the complete array once in the worst case.
• Space Complexity: O(1), as no additional space is required.

---

Problem 2 Count Pair Sum K

Find all the pairs in a sorted array whose sum is k.

Example:

A = {1, 2, 3, 4, 5, 6, 8}
k = 10

Ans:

(2, 8), (4, 6)

Warning

Please take some time to think about the solution approach on your own before reading further.....

Two Pointer Approach:

Case 1: When elements are distinct

• Use two pointer approach to find the first pair whose sum is 10.
• For array A, it will be (2, 8).
• As the elements are distinct, neither 2 nor 8 can make pair with any other pair whose sum is 10. So, increase the pointer i and decrease the pointer j and continue finding the pair whose sum is 10.
• The next pair with this approach would be (4, 6). Similary, move the pointers in required direction to find another pairs.
• Since, there aren't any more pairs. The final result would be: (2, 8) and (4, 6).

Pseudocode:

count = 0;
while (i < j) {
  if (A[i] + A[j] == k) {
    count++;
    i++, j--;
  } else if (A[i] + A[j] < k) {
    i++;
  } else {
    j--;
  }
}
return count;

Case 2: When elements are repeating (duplicates)

• Using Frequency Array:

  • Consider the array, ( A = {2, 3, 3, 10, 10, 10, 15} ) with a target sum ( k = 13 ).
  • Let's create the frequency map for the above. It would be - map ={[2 => 1], [3 => 2], [10 => 3], [15 => 1]}
  • Now, create an array (A' = {2, 3, 10, 15}) by taking only the unique elements from array (A).
  • Find the pair that contributes to the sum (13) in array (A'). The pair in this case would be (3, 10).
  • The frequency of (3) is (2) and the frequency of (10) is (3) in the original array. So, the total number of such pairs in the original array would be ( 2 * 3 = 6).
  • The key idea here is to transform the array with duplicate elements into an array of unique elements, find all the unique pairs that sum up to the target sum, and then use the frequencies of the elements in the original array to determine the count of all such pairs.

• Without using frequency array:

  • Consider array, A = {2, 3, 3, 5, 5, 7, 7, 10, 10, 10, 15} and k = 13
  • Find the pair whose sum is equal to k. In this case, (3, 10).
  • Now, count the number of 3s and 10s and multiply them to find the effective number of pairs, i.e., 2 * 3 = 6.
  • Change the position of i and j to next of last occurred 3 and 10, and continue the process.
  • Final result would be 6.

Pseudocode:

count = 0;
while (i < j) {
  if (A[i] + A[j] == k) {
    counti = 1, countj = 1;
    while (i < j && A[i] == A[i + 1]) {
      counti++;
      i++;
    }

    while (i < j && A[j] == A[j - 1]) {
      countj++;
      j--;
    }

    count = counti * countj;
    i++, j--;
  } else if (A[i] + A[j] < k) {
    i++;
  } else {
    j--;
  }
}
print(count)

---

Problem 3 Pair Difference K

Given a sorted integer array A and an integer k. Find any pair (i, j) such that A[j] - A[i] = k, i != j and k > 0.

Note: 0-based indexing

Example:

A[] =

Index	0	1	2	3	4	5	6
Value	-5	-2	1	8	10	12	15

k = 11

Ans: (2, 5) as A[5] - A[2] = 12 - 1 = 11 = k.

Brute Force Apporach:

Run two for loops and for every indices: i, j, check if difference is k.

• Time Complexity:

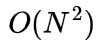, as we need to use two for loops.

• Space Complexity: O(1), as no additional space is required.

Binary Search Apporach

For all i, binary search and find k + A[i].

• Time Complexity: O(N * log(N)), as we need to apply binary search for every element in the worst case.

• Space Complexity: O(1), as no additional space is required.

---

Question

Given an array A is [5, 4, 2, 12, 1, 6] and K is 10.

Find any pair (i, j) such that

• A[j] - A[i] = k
• i != j

Note: 0-based indexing

Choices

• (2, 3)
• (5, 5)
• (0, 0)
• (3, 2)

Explanation:

The answer is (2, 3).

Since (2, 3) satisfies both the condition:

• A[3] - A[2] = 10
• 3 != 2

---

Pair Difference K Two Pointers Apporach

We have, A[] =

Index	0	1	2	3	4	5	6
Value	-5	-2	1	8	10	12	15

and k = 11

Where should we keep the pointers?

Option 1:

Let's start with keeping the pointers, i and j at the beginning and end of the array respectively, i.e., i = 0 and j = N - 1 = 6.

Observations:

• A[j] - A[i] = 15 - (-5) = 20 > k(11). So, to decrease the difference we need to either decrease A[j] or increase A[i].
• We know that, either we can increase pointer i or decrease pointer j. Increasing pointer i will increase the A[i] and similarly, decreasing pointer j will decrease the A[j].
• Since we do not have a single direction to move, we cannot eliminate any element. Therefore, placing the pointers at the beginning and the end isn't helpful.

Option 2:

Let's now place the pointers at (N - 2) and (N - 1) indices, i.e., i = N - 2 = 5 and j = N - 1 = 6.

Observations:

• A[i] = A[5] = 12 and A[j] = A[6] = 15. A[j] - A[i] = A[6] - A[5] = 15 - 12 = 3. Therefore, A[j] - A[i] < k
• Here, we either need to increase A[j] or decrease A[i]. To increase A[j], j should be increased but it isn't possible as j is already pointing to the last element. So, we can decrease i.
• Doing so will eliminate the 12 to be possible second value of the pair. This is true because from here, we can conclude that the largest element - A[i] < k. So, any element - A[i] < k because the array is sorted.
• Thus, N - 2 and N - 1 are the correct possible initial values of pointers.

Similary result can be obtained by starting with index 0 and 1.
So, let's place the pointers at 0 and 1 indices, i.e., i = 0 and j = 1.

Step 1: i = 0, j = 1

• A[i] = A[0] = -5 and A[j] = A[1] = -2. A[j] - A[i] = A[1] - A[0] = -2 - (-5) = 3.
  Therefore, A[j] - A[i] < k
• Here, we either need to increase A[j] or decrease A[i]. To decrease A[i], i should be decreased but it isn't possible as i is already pointing to the first element. So, we can increase j.

Step 2: i = 0, j = 2

• A[i] = A[0] = -5 and A[j] = A[2] = 1. A[j] - A[i] = A[2] - A[0] = 1 - (-5) = 6.
  Therefore, A[j] - A[i] < k
• Similarly, increasing j.

Step 3: i = 0, j = 3

• A[i] = A[0] = -5 and A[j] = A[3] = 8. A[j] - A[i] = A[3] - A[0] = 8 - (-5) = 13.
  Therefore, A[j] - A[i] > k.
• Since difference is greater than k, we need to decrease A[j] or increase A[i]. Hence, increasing i to increase A[i].

Step 4: i = 1, j = 3

• A[i] = A[1] = -2 and A[j] = A[3] = 8. A[j] - A[i] = A[3] - A[0] = 8 - (-2) = 10.
  Therefore, A[j] - A[i] < k.
• Since difference is less than k, we need to increase A[j] or decrease A[i]. Hence, increasing j to increase A[j].

Step 5: i = 1, j = 4

• A[i] = A[1] = -2 and A[j] = A[4] = 10. A[j] - A[i] = A[4] - A[0] = 10 - (-2) = 12.
  Therefore, A[j] - A[i] > k.
• Since difference is greater than k, we need to decrease A[j] or increase A[i]. Hence, increasing i to increase A[i].

Step 6: i = 2, j = 4

• A[i] = A[2] = 1 and A[j] = A[4] = 10. A[j] - A[i] = A[4] - A[0] = 10 - 1 = 9.
  Therefore, A[j] - A[i] < k.
• Since difference is less than k, we need to increase A[j] or decrease A[i]. Hence, increasing j to increase A[j].

Step 7: i = 2, j = 5

• A[i] = A[2] = 1 and A[j] = A[5] = 12. A[j] - A[i] = A[5] - A[0] = 12 - 1 = 11.
  Finally, A[j] - A[i] = k.
• Required pair: (i, j) = (2, 5).

Pseudocode:

i = 0, j = 1
while (j < n) {
  diff = A[j] - A[i];
  if (diff == k) {
    return (i, j);
  } else if (diff < k) {
    j++;
  } else {
    i--;
  }
}

Why the while loop condition should be j < n and not i < n?

It is based on assumption that i will always be <= j.

Proof:

Suppose we start with i = 0, j = 1 and after some steps j reaches x. To i cross j, i should first reach j. When i reaches j, then diff = 0. It is given that k > 0, so in order to achieve this, j should be increased, and hence i can never exceed j.

• Time Complexity: O(N), as we need to traverse the complete array once in the worst case.
• Space Complexity: O(1), as no additional space is required.

---

Problem 4 Check subarray with sum k

Given an integer array A and an integer k. Check if there exists a subarray with sum k

Example:

A = {1, 3, 15, 10, 20, 3, 23}; k = 33

Ans: True, because {10, 20, 3} sums upto 33.

A = {1, 3, 15, 10, 20, 3, 23}; k = 43

Ans: False, because no subarray exists that sums upto 43

Number of subarrays in an array of length n is n * (n + 1) / 2.

Brute Force Apporach:

Check every subarray sum (with carry forward approach)

• Time Complexity:

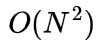, as we need to use two for loops.

• Space Complexity: O(1), as no additional space is required.

---

Question

If the given array is [1, 2, 5, 4, 3] and k is 9, does there exist a subarray with sum k?

Choices

• Not Exist
• Exist

Explanation:

Exist. The subarray is [5, 4].

---

Warning

Please take some time to think about the optimised approach on your own before reading further.....

Check subarray with sum k Two Pointers Approach

Given A = {1, 3, 15, 10, 20, 3, 23}, k = 33. Let's create prefix sum array for this:

Pf = {1, 4, 19, 29, 49, 52, 75}.

sum(i, j) = Pf[j] - Pf[i - 1], if i > 0 Pf[j], if i = 0

• To find the subarray with sum k, we can utilize the prefix sum array.
• For all j, if we check Pf[j], essentially, we have checked all the subarrays starting from 0. On the same line, if we check for Pf[j] - Pf[i - 1], we checked for every other subarray which doesn't starts with 0 in the array.
• Hence, we need to find the values of i and j for which Pf[j] - Pf[i - 1] = k. This is equivalent to finding a pair in a sorted array whose difference is k.

Prefix sum array is always sorted for positive integer array as the sum of every next subarray is increasing.

• Time Complexity: O(N)

  • Creating prefix sum array takes O(N) time.
  • Using two pointers approach to find the pair having diff as k also takes O(N).

• Space Complexity:

O(1), as no additional space is required if we use same array to create prefix sum array.

Dynamic Sliding Window Approach:

We can maintain a running sum based on the pointers position and check if it is equal to k.

Example:

A = {1, 3, 15, 10, 20, 3, 23, 33, 43}, k = 33

Step 1: i = 0, j = 0

• sum(i, j) = sum(0, 0) = A[0] = 1 < k. To increase the sum, we need to increase the length of subarray, so j++.

Step 2: i = 0, j = 1

• sum(i, j) = sum(0, 1) = A[0] + A[1] = 1 + 3 = 4 < k. To increase the sum, we need to increase the length of subarray, so j++.

Step 3: i = 0, j = 2

• sum(i, j) = sum(0, 2) = A[0] + A[1] + A[2] = 1 + 3 + 15 = 19 < k. To increase the sum, we need to increase the length of subarray, so j++.

Step 4: i = 0, j = 3

• sum(i, j) = sum(0, 3) = A[0] + A[1] + A[2] + A[3] = 1 + 3 + 15 + 10 = 29 < k. To increase the sum, we need to increase the length of subarray, so j++.

Step 5: i = 0, j = 4

• sum(i, j) = sum(0, 4) = A[0] + A[1] + A[2] + A[3] + A[4] = 1 + 3 + 15 + 10 + 20 = 49 > k. To decrease the sum, we need to decrease the length of subarray. This can either be done by i++ or j--. If we do j--, we will be at the same stage at step 4, which isn't helpful. So, we need to do i++ to decrease the length and effectively the sum.

Step 6: i = 1, j = 4

• sum(i, j) = sum(1, 4) = A[1] + A[2] + A[3] + A[4] = 3 + 15 + 10 + 20 = 48 > k. Again, we need to decrease the length to decrease the sum.

What shall we do here: i++ or j--?

We know that, sum (0, 3) < k. Therefore, sum(1, 3) will definitely be less than k. Therefore, i++ is correct way out here.

Step 7: i = 2, j = 4

• sum(i, j) = sum(2, 4) = A[2] + A[3] + A[4] = 15 + 10 + 20 = 45 > k. Again, we need to decrease the length to decrease the sum. As discussed above, do i++.

Step 8: i = 3, j = 4

• sum(i, j) = sum(3, 4) = A[3] + A[4] = 10 + 20 = 30 < k. To increase the array length, do j++.

Step 9: i = 3, j = 5

• sum(i, j) = sum(3, 5) = A[3] + A[4] + A[5] = 10 + 20 + 3 = 33 = k. We have found the required subarray.

Pseudocode

i = 0, j = 0, sum = A[0]

while (j < n) {
  if (sum == k) {
    return true;
  } else if (sum < k) {
    j++;
    if (j == n) { // To make sure index is not out of bounds
      break;
    }

    sum += A[j];
  } else {
    sum -= A[i];
    i++;
    if (i > j) { // To make sure i never exceeds j
      break;
    }
  }
}

return false;

• Time Complexity: O(N), as in the worst case, complete array will be traversed.

• Space Complexity: O(1), as no additional space is required if we use same array to create prefix array.

---

Problem 5 Container with most Water

Given an integer array A where array elements represent the height of the wall. Find any two walls that can form a container to store the maximum amount of water.

Example: A = {4, 2, 10, 6, 8, 2, 6, 2}

Ans: 24. (Maximum amount of water stored between walls at idx (1 and 7) or between idx (3 and 7))

Since area = height * width, therefore
Amount of water stored between any two walls A[i] and A[j] = min(A[i], A[j]) * (j - i), where height = min(A[i], A[j]) and width = (j - i).

Note: height = min(A[i], A[j]), as water can be stored upto minimum height of the wall, and width = (j - i), i.e., the difference between the position of walls.

Brute Force Apporach:

Choose all the pair of walls, calculate the amount of water stored between them and find the maximum.

• Time Complexity: O(N²), as we need to use two for loops.
• Space Complexity: O(1), as no additional space is required.

---

Question

What is the water trapped between 2 walls at index L and R.
Array A gives the heights of buildings
Chose the correct answer

Choices

• (R - L) * min(A[L], A[r])
• (R - L)* max(A[L], A[r])
• (R - L + 1) * min(A[L], A[r])
• (R - L + 1) * max(A[L], A[r])

Explanation:

The answer is (R - L) * min(A[L], A[r]).

• Amount of water stored between any two walls A[L] and A[R] = min(A[L], A[R]) * (R - L)

where height = min(A[L], A[R])
width = (R - L).

---

Warning

Please take some time to think about the optimised approach on your own before reading further.....

Container with most Water Two Pointer Approach

• Since area = height * width. To achieve the maximum area, we should find the maximum values for height and width.
• Let's start with maximum width, so keep i = 0 and j = n - 1.
• height = min(A[i], A[j]). So, in order to increase the height, we should move in the direction of increasing the minimum height.

Example:

A[] =

Index	0	1	2	3	4	5	6	7
Value	4	2	10	6	8	2	6	2

Step 1: i = 0, j = 7, max_area = -1 (Initially)

• height = min(A[0], A[7]) = min(4, 2) = 2.
  width = j - i = 7 - 0 = 7.
  area = height * width = 2 * 7 = 14.
  max_area = max(max_area, area) = max(-1, 14) = 14.
  To increase the area, we need to move in direction of increasing the minimum height. Since min height is 2, this can be increased by doing j--.

Step 2: i = 0, j = 6, max_area = 14

• height = min(A[0], A[6]) = min(4, 6) = 4.
  width = j - i = 6 - 0 = 6.
  area = height * width = 4 * 6 = 24.
  max_area = max(max_area, area) = max(14, 24) = 24.
  To increase the area, we need to move in direction of increasing the minimum height. Since min height is 4, this can be increased by doing i++.

Step 3: i = 1, j = 6, max_area = 24

• height = min(A[1], A[6]) = min(2, 6) = 2.
  width = j - i = 6 - 1 = 5.
  area = height * width = 2 * 5 = 10.
  max_area = max(max_area, area) = max(24, 10) = 24.
  To increase the area, we need to move in direction of increasing the minimum height. Since min height is 2, this can be increased by doing i++.

Step 4: i = 2, j = 6, max_area = 24

• height = min(A[2], A[6]) = min(10, 6) = 6.
  width = j - i = 6 - 2 = 4.
  area = height * width = 6 * 4 = 24.
  max_area = max(max_area, area) = max(24, 24) = 24.
  To increase the area, we need to move in direction of increasing the minimum height. Since min height is 6, this can be increased by doing j--.

Step 5: i = 2, j = 5, max_area = 24

• height = min(A[2], A[5]) = min(10, 2) = 2.
  width = j - i = 5 - 2 = 3.
  area = height * width = 2 * 3 = 6.
  max_area = max(max_area, area) = max(24, 6) = 24.
  To increase the area, we need to move in direction of increasing the minimum height. Since min height is 2, this can be increased by doing j--.

Step 6: i = 2, j = 4, max_area = 24

• height = min(A[2], A[4]) = min(10, 8) = 8.
  width = j - i = 4 - 2 = 2.
  area = height * width = 8 * 2 = 16.
  max_area = max(max_area, area) = max(24, 16) = 24.
  To increase the area, we need to move in direction of increasing the minimum height. Since min height is 2, this can be increased by doing j--.

Step 7: i = 2, j = 3, max_area = 24

• height = min(A[2], A[3]) = min(10, 6) = 6.
  width = j - i = 3 - 2 = 1.
  area = height * width = 6 * 1 = 6.
  max_area = max(max_area, area) = max(24, 6) = 6.
  After this, moving any of i or j will yield width as 0. Hence, we stop the execution and final ans is 24.

Pseudocode:

i = 0, j = n - 1;
while (i < j) {
  area = min(A[i], A[j]) * (j - 1);
  if (A[i] < A[j]) {
    i++;
  } else if (A[i] > A[j]) {
    j--;
  } else {
    i++, j--; // Doesn't matter if we move only i or j or both
  }
}
return area;

• Time Complexity: O(N), as we are traversing the complete array only once.
• Space Complexity: O(1), as no additional space is required.

---