2D Matrices¶

Definition¶

A 2D matrix is a specific type of 2D array that has a rectangular grid of numbers, where each number is called an element. It is a mathematical structure that consists of a set of numbers arranged in rows and columns. 2D matrix can be declared as:

int mat[N][M];

int is the datatype.
mat is the matrix name.
N is the number of rows in matrix.
M is the number of columns in matrix.

mat[i][j] represents the element present in the i-th row of j-th column.

Below is the pictorial representation of 2D matrix.

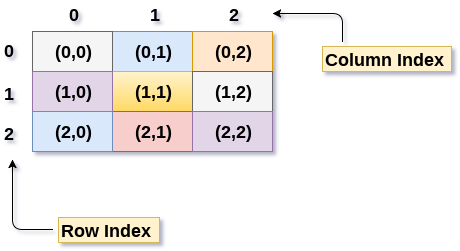
Note: A matrix having N rows and M columns can store N*M elements.

Question¶

Given a matrix of size NxM. What will be the index of the top right cell? Choose the correct answer

Choices

0,0
0,M
M-1,0
0,M-1

Question¶

Given a matrix of size NxM. What will be the index of the bottom right cell?

Choose the correct answer

Choices

N,M
M,N
N-1,M-1
M-1,N-1

Question 1 : Given a matrix print row-wise sum¶

Problem Statement

Given a 2D matrix mat[N][M], print the row-wise sum.

TestCase¶

Input:

mat[3][4] = {
    {1,2,3,4},
    {5,6,7,8},
    {9,10,11,12}
}

Output:

10
26
42

Approach¶

The approach is to traverse each row and while traversing take the sum of all the elements present in that row.

Pseudocode:¶

function SumRow(int mat[N][M]) {
    for (int i = 0; i < N; i++) {
        int sum = 0;
        for (int j = 0; j < M; j++) {
            sum = sum + mat[i][j];
        }
        print(sum);
    }
}

Question¶

What is the time and space complexity of to calculate row-wise sum for a matrix of size N*M? Choose the correct answer

Choices

TC: O(N^2), SC: O(n)
TC: O(N^2), SC: O(1)
TC: O(N^M), SC: O(n)
TC: O(N*M), SC: O(1)

Since we are iterating over all the elements just once, hence

Time Complexity: O(N*M).

We are not using any extra space,

Space Complextiy: O(1).

Question 2 : Given a matrix print col-wise sum¶

Given a 2D matrix mat[N][M], print the column-wise sum.

TestCase

mat[3][4] = {
    {1,2,3,4},
    {5,6,7,8},
    {9,10,11,12}
}

Output

15 18 21 24

Warning

Please take some time to think about the solution approach on your own before reading further.....

Approach¶

While traversing each column, we can calculate sum of all the elements present in that column.

Pseudocode¶

function SumColumn(int mat[N][M]) {
    for (int j = 0; j < M; j++) {
        int sum = 0;
        for (int i = 0; i < N; i++) {
            sum = sum + mat[i][j];
        }
        print(sum);
    }
}

Complexity¶

Time Complexity: O(N*M).
Space Complextiy: O(1).

Question 3 : Given a square matrix print diagonals¶

Given a matrix 2D square matrix mat[N][N], print diagonals.

How many main Diagonals are there in a square matrix? 2.

Principal Diagonal: From top left to bottom right.
Anti Diagonal: From top right to bottom left.

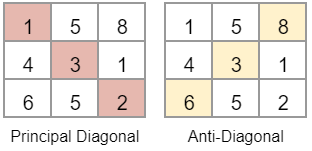
First, let's print Principal Diagonal

TestCase

mat[3][3] = {
    {1,2,3},
    {5,6,7},
    {9,10,11}
}

Output:

1 6 11

Question 3 Approach¶

Pseudocode:¶

function PrintDiagonal(int mat[N][N]) {
    int i = 0;
    while (i < N) {
        print(mat[i][i]);
        i = i + 1;
    }
}

Question¶

Given a matrix of size NxN. What will be the time complexity to print the diagonal elements? Chose the correct answer

Choices

O(N*sqrt(N))
O(N)
O(N^2)
O(NlogN)

Since i starts at 0 and goes till N-1, hence there are total N iterations.

Time Complexity: O(N).
Space Complextiy: O(1).

Given square matrix, print Anti-diagonal¶

TestCase

mat[3][3] = {
    {1,2,3},
    {5,6,7},
    {9,10,11}
}

Output:

3 6 9

Pseudocode:¶

function PrintDiagonal(int mat[N][N]) {
    int i = 0, j = N - 1;
    while (i < N) {
        print(mat[i][j]);
        i++;
        j--;
    }
}

Complexity¶

Time Complexity: O(N).
Space Complextiy: O(1).

Question 4 Print diagonals in a matrix (right to left)¶

Problem Statement

Given a 2D matrix mat print all the elements diagonally from right to left

TestCase

mat[3][4] = {
    {1,2,3,4},
    {5,6,7,8},
    {9,10,11,12}
}

Output:

Question¶

Given a matrix of size N*M, how many Right to Left diagonals will be there?

Choose the correct Options

Choices

N*M
N+M
N+M-1
N+M+1
M diagonals are starting from first row.
N diagonals start from last column.
There is a common diagonal at index 0, M-1.

So, total count = N+M-1 Let's take an example as shown below:

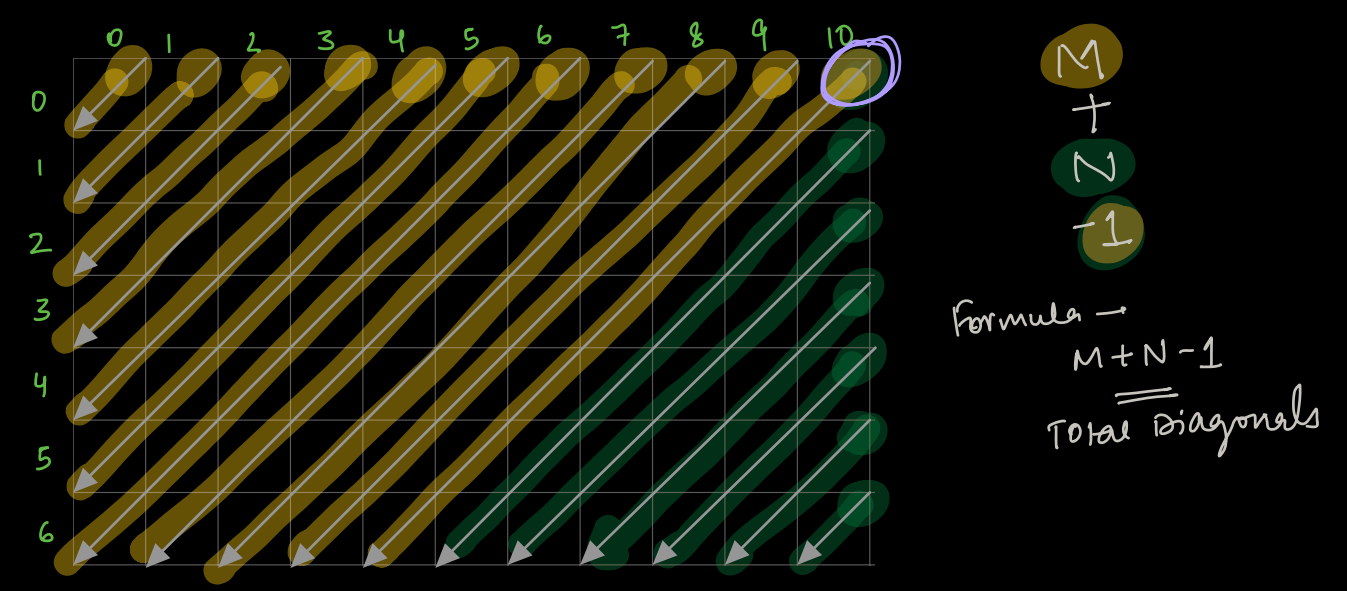
Question¶

Given a matrix of size 4x5, how many Right to Left diagonals will be there? Choose the correct answer

Choices

8
11
9
10

Question 4 Approach¶

Warning

Please take some time to think about the solution approach on your own before reading further.....

For every start of the diagonal, how do the indices change when we iterate over it? Row number increments by 1 and column number decrements by 1 as shown in the diagram.

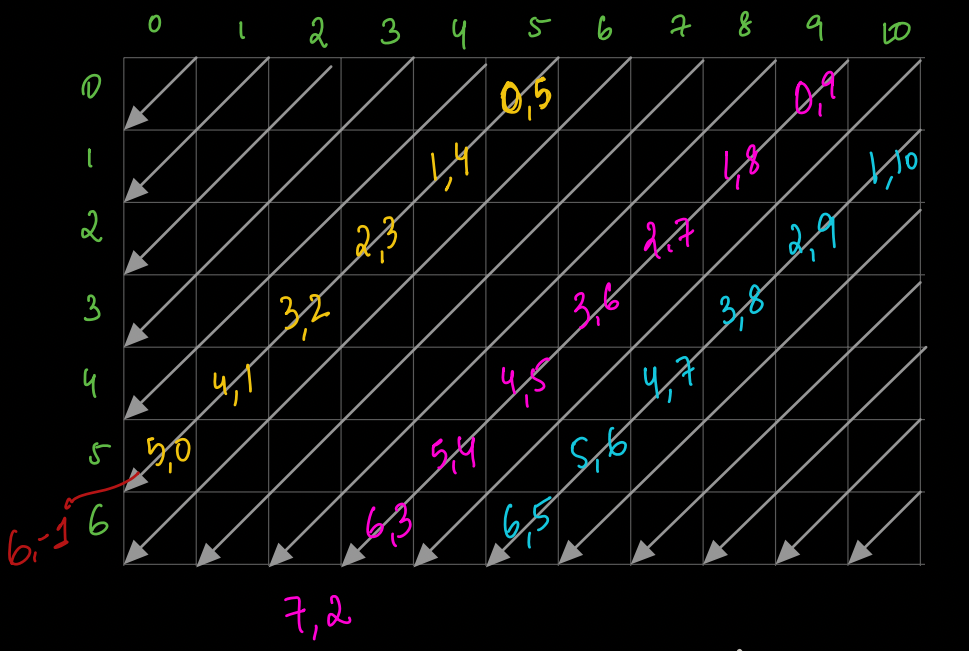
Pseudocode¶

function print_diagonal_elements(A[N][M]) {
    //print all diagonals starting from 0th row
    i = 0
    for (j = 0; j < M; j++) {
        s = i;
        e = j;
        while (s < N && e >= 0) {
            print(A[s][e])
            s++
            e—
        }
        print(“\n”)
    }

    //print all diagonals starting from last column
    j = M - 1
    for (i = 1; i < N; i++) {
        s = i;
        e = j;
        while (s < N && e >= 0) {
            print(A[s][e])
            s++
            e—
        }
        print(“\n”)
    }
}

Question¶

Time Complexity of printing all the diagonals of a matrix of dimensions N X M? Choose the correct answer

Choices

O(N^2 * M^2)
O(N^2 + M^2)
O(N + M)
O(N * M)

Question 5 : Transpose of a square matrix¶

Problem Statement

Given a square 2D matrix mat[N][N], find transpose.

Transpose of matrix

The transpose of a matrix is a new matrix obtained by interchanging the rows and columns of the original matrix.

TestCase

mat[3][3] = {
    {1,2,3},
    {5,6,7},
    {9,10,11}
}

Output:

{
{1,5,9},
{2,6,10},
{3,7,11}
}

Warning

Please take some time to think about the solution approach on your own before reading further.....

Question 5 Approach¶

Observation¶

After performing the transpose, what is same in the original matix and its transpose ? The diagonal that starts from (0,0) is same.

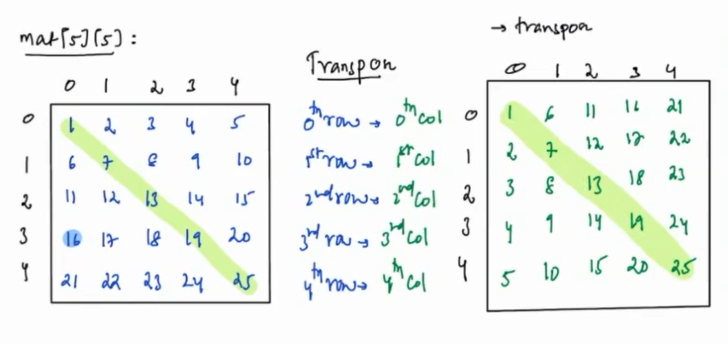
Along the diagonals, the elements have swapped their positions with corresponding elements.

PseudoCode¶

function find_transpose(matrix[N][N]){
    for(int i = 0; i < N; i++){
        for(int j = i + 1; j < N; j++){
            swap(matrix[i][j],matrix[j][i]);
        }
    }
}

Note: If we start j at 0, the matrix will come back to its original position.

Question¶

What is the time and space complexity to find transpose of a square matrix? Chose the correct answer

Choices

TC: O(N), SC: O(n)
TC: O(N^2), SC: O(n)
TC: O(N^2), SC: O(1)
TC: O(N), SC: O(1)

Complexity

Time Complexity: O(N^2).
Space Complextiy: O(1).

Question 6 Rotate a matrix to 90 degree clockwise¶

Problem Statement

Given a matrix mat[N][N], rotate it to 90 degree clockwise.

TestCase

{
{1,2,3},
{4,5,6},
{7,8,9}
}

Output

{
{7,4,1},
{8,5,2},
{9,6,3}
}

Question 6 Approach¶

Hint:¶

What if we first find the transpose of the matrix?
Is there any relation between rotated matrix and transposed matrix ?

Warning

Using the Hints, please take some time to think about the solution approach on your own before reading further.....

Observation:¶

Yes, if we reverse all the rows, then it will become rotated matrix.

The rotated matrix looks like:

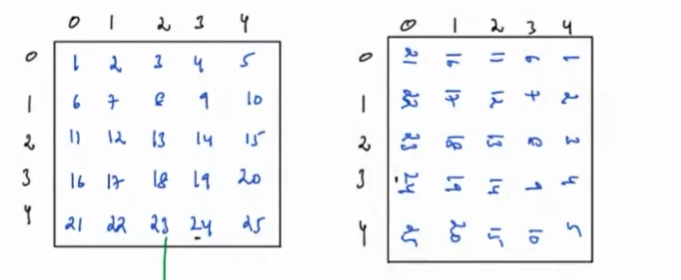
Transpose and rotated matrix:

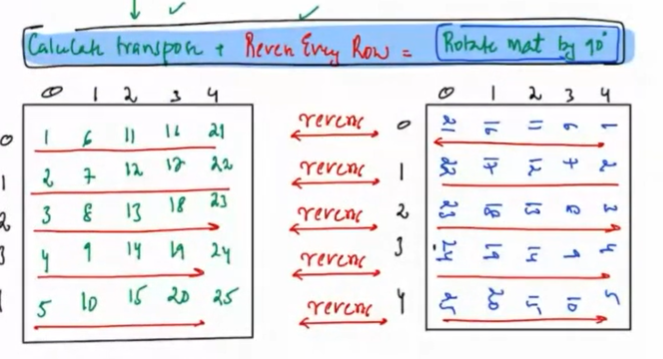
PseudoCode¶

Function rotate(int mat[N][N]) {
    mat = transpose(mat);
    for (int i = 0; i < N; i++) {
        reverse(mat[i]);
    }
    return mat;
}

Complexity¶

Time Complexity: O(N*N).
Space Complextiy: O(1).