Bit Manipulation Basics¶

Decimal Number System¶

The decimal system, also known as the base-10 system, is the number system we use in our everyday lives.
It is called base-10 because a single digit can take 10 values from 0 to 9.

The position of each digit in a decimal number represents a different power of 10.

For example,

342  = 300 + 40 + 2 = 3*10^2 + 4*10^1 + 2*10^0

2563 = 2000 + 500 + 60 + 3 = 2*10^3 + 5*10^2 + 6*10^1 + 3*10^0

Binary Number System¶

The binary system, also known as the base-2 system, is used in digital electronics and computing.
It has only two digits, which are 0 and 1.

In the binary system, each digit represents a different power of 2.

For example,

110 = 1*2^2 + 1*2^1 + 0*2^0 = 4 + 2 + 0 = 6

1011 = 1*2^3 + 0*2^2 1*2^1 + 1*2^0 = 8 + 0 + 2 + 1 = 11

Binary to Decimal Conversion¶

For this conversion, we need to multiply each digit of the binary number by the corresponding power of 2, and then add up the results.

Example 1:

Convert binary number 1101 to decimal number.

Starting from the rightmost digit, we have:

1 * 2^0 = 1
0 * 2^1 = 0
1 * 2^2 = 4
1 * 2^3 = 8

Adding up the results, we get:

1 + 0 + 4 + 8 = 13

Therefore, the decimal equivalent of the binary number 1101 is 13.

Example 2:

Convert binary number 10101 to decimal number.

Starting from the rightmost digit, we have:

1 * 2^0 = 1
0 * 2^1 = 0
1 * 2^2 = 4
0 * 2^3 = 0
1 * 2^4 = 16

Adding up the results, we get:

1 + 0 + 4 + 0 + 16 = 21

Therefore, the decimal equivalent of the binary number 10101 is 21.

Question¶

What is the decimal representation of this binary number: 1011010

Choices

45
90
94
130

Explanation:

Starting from the rightmost digit, we have:

0 * 2^0 = 0
1 * 2^1 = 2
0 * 2^2 = 0
1 * 2^3 = 8
1 * 2^4 = 16
0 * 2^5 = 0
1 * 2^6 = 64
Adding up the results, we get: 0 + 2 + 0 + 8 + 16 + 0 + 64 = 90
Therefore, the decimal representation of the binary number 1011010 is 90.

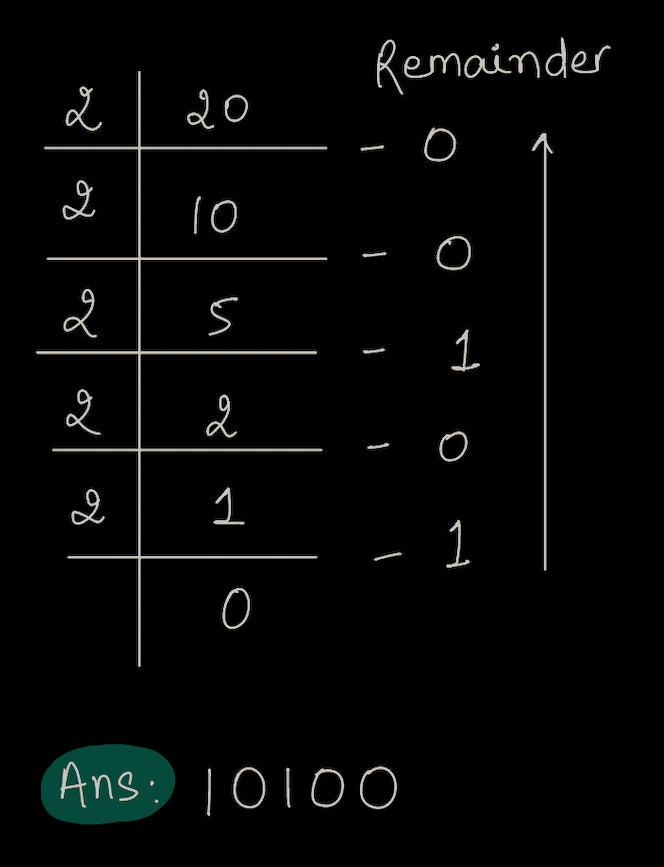
Decimal to Binary Conversion¶

We can solve it using long division method, for which we need to repeatedly divide the decimal number by 2 and record the remainder until the quotient becomes 0.

Example:

Convert decimal number 20 to binary number.

Question¶

What is the binary representation of 45 ?

Choices

101100
101110
101111
101101

Explanation: Here are the steps to convert decimal number 45 to binary:

Addition of Decimal Numbers¶

Example -

Calculate => (368 + 253)

Explanation:

Start by adding the rightmost digits: 8 + 3 = 11 (digit = 11%10 = 1, carry 11/10 = 1)
Next column: 1 + 6 + 5 = 12 (digit = 12%10 = 2, carry 12/10 = 1)
Final column: 1 + 3 + 4 = 8 (digit = 8%10 = 8, carry 8/10 = 0)

Therefore, answer is 821.

Addition of Binary Numbers¶

Example 1:

	1	0	1	0	1
+		1	1	0	1
1	0	0	0	1	0

Explanation:

d = answer digit, c = carry

From right, 1 + 1 = 2 (d = 2%2=0, c = 2/2 = 1)
Next: 1 + 0 + 0 = 1 (d = 1%2=1, c = ½ = 0)
Next: 0 + 1 + 1 = 2 (d = 2%2=0, c = 2/2 = 1)
Next: 1 + 0 + 1= 2 (d = 2%2=0, c = 2/2 = 1)
Final: 1 + 1 = 2 (d = 2%2=0, c = 2/2 = 1)
Finally, 1 carry is remaining, so write 1.

The result is 100010 in binary.

Example 2:

	1	1	0	1	0	1
+	1	0	0	1	1	0
1	0	1	1	0	1	1

Explanation:

d = answer digit, c = carry

From Right: 1 + 0 = 1 (d: 1%2 = 1, c: ½ = 0)
Next column: 0 + 0 + 1 = 1 (d: 1%2 = 1, c: ½ = 0)
Next column: 0 + 1 + 1 = 2 (d: 2%2 = 0, c: 2/2 = 1)
Next column: 1 + 0 + 0 = 1 (d: 1%2 = 1, c: ½ = 0)
Next column: 0 + 1 + 0 = 1 (d: 1%2 = 1, c: ½ = 0)
Next column: 0 + 1 + 1 = 2 (d: 2%2 = 0, c: 2/2 = 1)
Finally, 1 carry is remaining, so write 1.

The result is 1011011 in binary.

Question¶

What is the sum of these binary numbers: 10110 + 00111

Choices

11111
10101
11011
11101

Explanation:

d = answer digit, c = carry

Start by adding the rightmost bits: 0 + 1 = 1 (d: 1%2 = 1, c: ½ = 0)
Next column: 0 + 1 + 1 = 2 (d: 2%2 = 0, c: 2/2 = 1)
Next column: 1 + 1 + 1 = 3 (d: 3%2 = 1, c: 3/2 = 1)
Next column: 1 + 0 + 0 = 1 (d: 1%2 = 1, c: ½ = 0)
Final column: 0 + 1 + 0 = 1 (d: 1%2 = 1, c: ½ = 0)

The result is 11101 in binary.

Bitwise Operators¶

Bitwise operators are used to perform operations on individual bits of binary numbers.
They are often used in computer programming to manipulate binary data.
In bitwise operations, 0 -> false/unset and 1 -> true/set

AND (&)¶

This operator takes two binary numbers and performs a logical AND operation on each pair of corresponding bits.
The resulting bit in the output is 1 if and only if both the corresponding bits in the input are 1. Otherwise, the resulting bit is 0.
The symbol for AND operator is '&'.

0 & 0 = 0
1 & 0 = 0
0 & 1 = 0
1 & 1 = 1

OR (|)¶

This operator takes two binary numbers and performs a logical OR operation on each pair of corresponding bits.
The resulting bit in the output is 1 if either one or both of the corresponding bits in the input are 1. Otherwise, the resulting bit is 0.
The symbol for OR operator is '|'.

0 | 0 = 0
1 | 0 = 1
0 | 1 = 1
1 | 1 = 1

XOR (^)¶

This operator takes two binary numbers and performs a logical XOR (exclusive OR) operation on each pair of corresponding bits.
The resulting bit in the output is 1 if the corresponding bits in the input are different. Otherwise, the resulting bit is 0.
The symbol for XOR operator is '^'.

0 ^ 0 = 0
1 ^ 0 = 1
0 ^ 1 = 1
1 ^ 1 = 0

NOT(!/~)¶

This operator takes a single binary number and performs a logical NOT operation on each bit.
The resulting bit in the output is the opposite of the corresponding bit in the input.
The symbols for NOT operator are '~' or '!'.

~0 = 1
~1 = 0

Bitwise Operations Example¶

Example 1:

5 & 6
//Binary representation
5 -> 101
6 -> 110
// Bitwise AND operation
101 & 110 = 100 = 4

Example 2:

20 & 45
//Binary representation
20 -> 010100
45 -> 101101
// Bitwise AND operation
010100 & 101101 = 111101 = 61

Example 3:

92 & 154
//Binary representation
92 -> 01011100
154 -> 10011010
// Bitwise OR operation
01011100 | 10011010 = 11011110 = 222

Example 4:

~01011100
//Binary representation
92 -> 01011100
// Bitwise NOT operation
~01011100 = 10100011 = 163

Example 5:

92 ^ 154
//Binary representation
92 -> 01011100
154 -> 10011010
// Bitwise XOR operation
01011100 ^ 10011010 = 11000110 = 198

Question¶

What is the value of A ^ B (i.e. A XOR B) where, A = 20 and B = 45?

Choices

4
20
57
61

Explanation:

A = 20 = 00010100 (in binary)
B = 45 = 00101101 (in binary)

Performing XOR on each pair of bits, we get:

00010100 ^ 00101101 = 00111001

Therefore, the value of A XOR B is 00111001, which is 57 in decimal format.

Binary Representation of Negative numbers¶

To convert a negative number to its binary representation, we can use two's complement representation.

It works as follows -

Convert the absolute value of number to Binary representation.
Invert all the bits of number obtained in step 1.
Add 1 to the number obtained in step 2.

Example of converting the negative number -5 to its 8-bit binary representation:

5 to binary representation:0000 0101
Invert all the bits:0000 0101 -> 1111 1010
Add 1 to the inverted binary representation: 1111 1010 + 0000 0001 = 1111 1011

Note:

The MSB has a negative base and that is where the negative sign comes from.
In case of positive number, MSB is always 0 and in case of negative number, MSB is 1.

Question¶

What is the binary representation of -3 in 8-bit signed integer format? Choose the correct answer

Choices

11111101
01111101
00000011
10101010

Question¶

What is the binary representation of -10 in 8-bit signed integer format? Choose the correct answer

Choices

11110110
11110111
11111110
10101010

Range of Data Types¶

What is the minimum & maximum no. that can be stored in the given no. of bits?

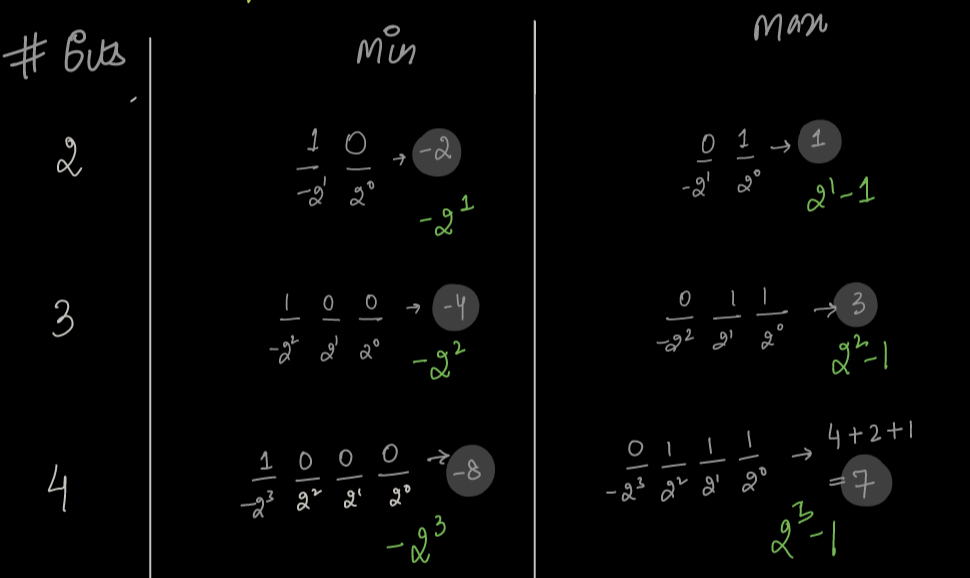
Generalisation for N Bits:

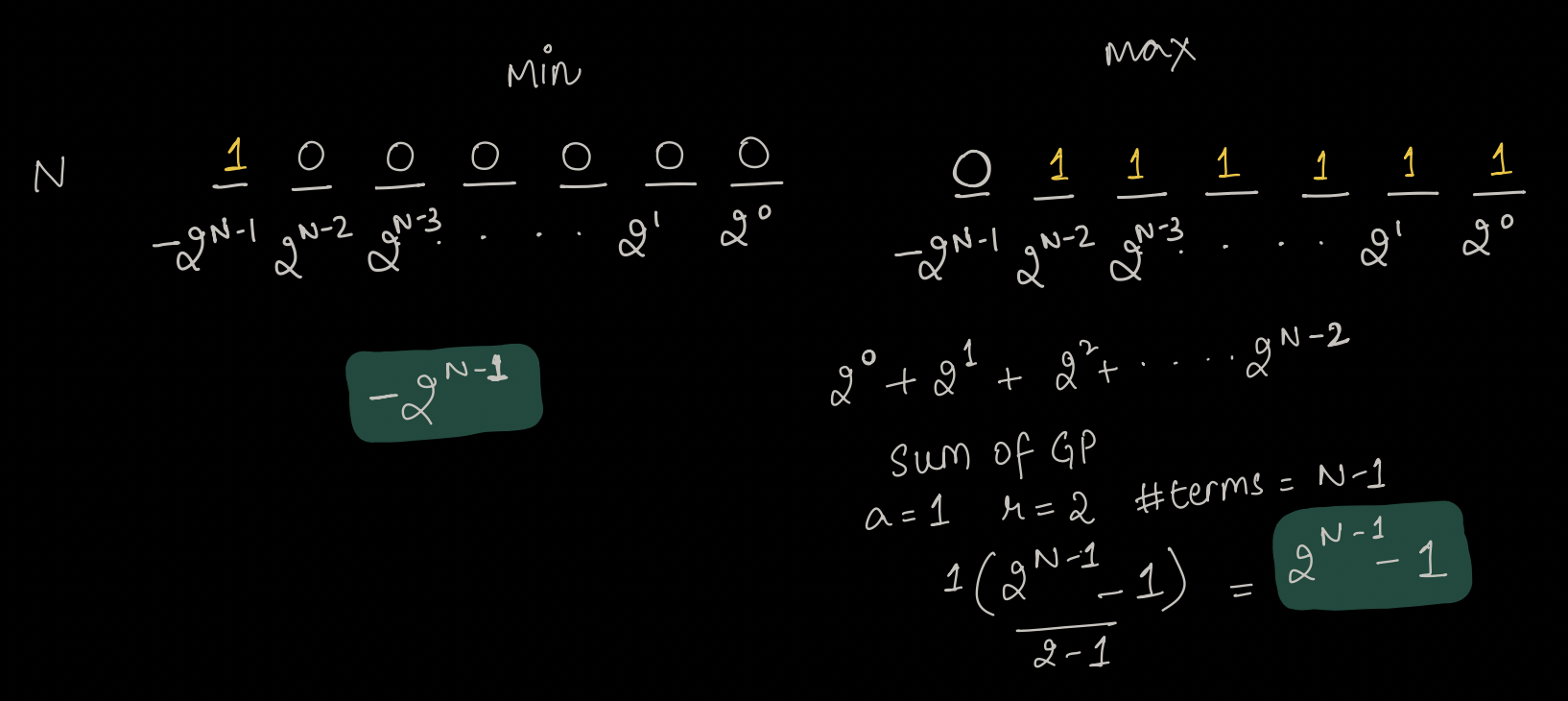
So, in general we can say that the {minimum,maximum} number in n-bit number is {-2^N-1 , 2^N-1-1}.

Integer(32-bit number)¶

Integer is the 32 bit number. Its range is {-2^32-1 , 2^32-1-1}.

Long(64-bit number)¶

Long is the 64 bit number. Its range is {-2^64-1 , 2^64-1-1}.

Approximation¶

Approximation is done to better approximate the range of values that can be stored in integer or long.

For integer,

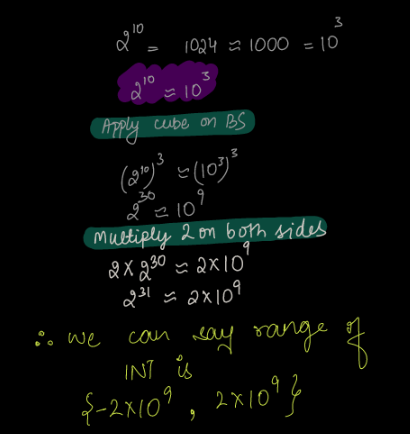
For long,

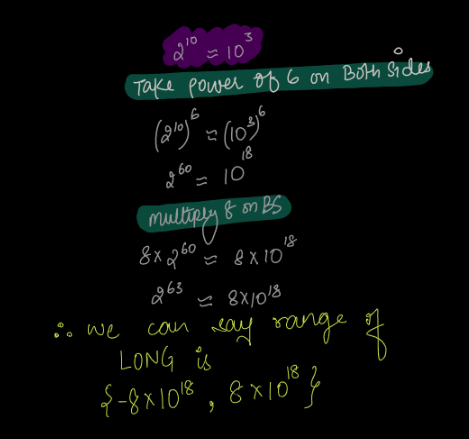
Importance of Constraints¶

Let's understand the importance of constraints using example.

Suppose we have two integers as

a = 10^5
b = 10^6

What will be the value of c ?

TRY 1:¶

int c = a*b

It will Overflow, i.e c will contain wrong value.

Fails, the Reason:

The calculation happens at ALU.
If we provide ALU with two INT, it calculates result in INT.
Therefore, a*b will overflow before even getting stored in c.

TRY 2:¶

Say, we change the data type of c to long, what will be the value of c?

long c = a*b

Fails, the Reason:

c would contain overflowed value since a*b will overflow at the time of calculation, therefore there's no use to change datatype of c from INT to LONG.

TRY 3:¶

What if we typecast a*b to long as below?

long c = long (a*b)

Fails, the Reason:

Already overflown, hence no use to typecast later.

TRY 4:¶

What if we change the equation as shown below?

long c = (long) a * b

This is the correct way to store.

WORKS, the Reason:

Here, we have typecasted a to long before multiplying with b.
If we send one INT and one LONG, ALU calculates answer in LONG.

Question¶

Given an array of size N, calculate the sum of array elements.

Constraints:

1 <= N <= 10⁵
1 <= A[i] <= 10⁶

Is the following code correct ?

int sum = 0;
for (int i = 0; i < N; i++) {
    sum = sum + A[i];
}
print(sum)

We should look at constraints.

As per constraint, range of sum will be as follows -

1 <= sum <= 10¹¹

The above code is incorrect since sum can be as big as 10¹¹ which can't be stored in INTEGER.
Hence, we should change dataType of "sum" to LONG.