Carry Forward & Subarrays

Problem 1 : Count of Pairs ag

Given a string s of lowercase characters, return the count of pairs (i,j) such that i < j and s[ i ] is 'a' and s[ j ] is 'g'.

Example 1

String s = "abegag"
Ans = 3

Explanation:

Here, [i,j] such that i<j and s[i] is 'a' and s[j] is 'g' are [0,3], [0,5] and [4,5]. So ans would be 3.

Question

What is the count of a,g pairs in the array:- s = "acgdgag"

Choices

• 4
• 3
• 5
• 2

Explanation:

Here, [i,j] such that i<j and s[i] is 'a' and s[j] is 'g' are [0,2], [0,4], [0,6] and [5,6]. So ans would be 4.

Question

How many ag pairs are in this string? s = "bcaggaag"

Choices

• 5
• 4
• 3
• 6

Explanation:

Here, [i,j] such that i<j and s[i] is 'a' and s[j] is 'g' are [2,3], [2,4], [2,7], [5,7] and [6,7]. So ans would be 5.

Warning

Please take some time to think about the brute force approach on your own before reading further.....

Problem 1 : Brute Force Solution

For every 'a', we need to find the count of g's on the right side of a. So, we need to have nested loops.

Pseudocode

int count_ag(string s) {
    int result = 0;
    for (int i = 0; i < n; i++) {
        if (s[i] == 'a') {
            for (int j = i + 1; j < n; j++) {
                if (s[j] == 'g') {
                    result++;
                }
            }
        }
    }
    return result;
}

Time and Space Complexity

Time Complexity : O(n^2)
Space Complexity : O(1)

Problem 1 Optimised solution

Observation:

• For every 'g', we need to know the count of 'a' on left side of 'g'.
• We will store the count of 'a' and whenever 'g' is encountered, we will add the count of 'a' to the result.

Dry Run

Example: "acbagkagg"

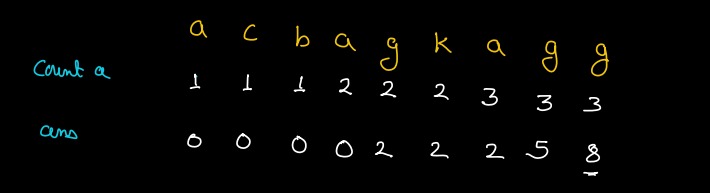
Pseudocode

int count_ag(string s) {
    int result = 0;
    int count_a = 0;
    for (int i = 0; i < n; i++) {
        if (s[i] == 'a') {
            count_a++;
        } else if (s[i] == 'g') {
            result += count_a;
        }
    }
    return result;
}

Time and Space Complexity

What will be T.C and S.C for this approach?

Time Complexity : O(n)
Space Complexity : O(1)

Introduction to Subarrays

Definition

A subarray is a contiguous part of an array. It is formed by selecting a range of elements from the array. A subarray can have one or more elements and must be a contiguous part of the original array.

Example

Consider the following array of integers:

4	1	2	3	-1	6	9	8	12

• 2, 3, -1, 6 is a subarray of length 4.
• 9 is a subarray of single element.
• 4, 1, 2, 3, -1, 6, 9, 8, 12 is a subarray consisting of all the array elements.
• 4, 12 is not a subarray because loop does not count as subarray.
• 1, 2, 6 is not a subarray beacuse the array elements must be contiguous.
• 3, 2, 1, 4 is not a subarray because order of the elements in a subarray should be same as in the array.

Question

A[] = { 2, 4, 1, 6, -3, 7, 8, 4}
Which of the following is a valid subarray?

Choices

• {1, 6, 8}
• {1, 4}
• {6, 1, 4, 2}
• {7, 8, 4}

Explanation:

{1, 6, 8} & {1, 4} are not contiguous parts of array. {6, 1, 4, 2} is not in the same order as in original array. Only {7, 8, 4} is a valid subarray.

Representation of a Subarray

Representation of a Subarray

A Subarray can be uniquely represented in following ways:

1. By specifying the start and end index of the subarray.
2. By specifying the start index and length of the subarray.

If we consider the same array from the above example,

4	1	2	3	-1	6	9	8	12

The subarray 2, 3, -1, 6 can be represented as

• the range of elements starting at index 2 and ending at index 5 (0-based indexing).
• the range of elements having length of 4 with start index as 2.

Question

How many subarrays of the following array start from index 0
[4, 2, 10, 3, 12, -2, 15]

Choices

• 6
• 7
• 21
• 36

[4] (starting from index 0)
[4, 2]
[4, 2, 10]
[4, 2, 10, 3]
[4, 2, 10, 3, 12]
[4, 2, 10, 3, 12, -2]
[4, 2, 10, 3, 12, -2, 15]
Therefore, there are a total of 7 subarrays that start from index 0.

Question

How many subarrays of the following array start from index 1
[4, 2, 10, 3, 12, -2, 15]

Choices

• 6
• 7
• 21
• 36

[2] (starting from index 1)
[2, 10]
[2, 10, 3]
[2, 10, 3, 12]
[2, 10, 3, 12, -2]
[2, 10, 3, 12, -2, 15]
Therefore, there are a total of 6 subarrays that start from index 1.

Formula to count no. of subarrays

No. of subarrays starting from index 0 = n
No. of subarrays starting from index 1 = n-1
No. of subarrays starting from index 2 = n-2
No. of subarrays starting from index 3 = n-3

...........

...........

No. of subarrays starting from index n-1 = 1

So, Using the formula for the sum of an arithmetic series, total number of subarrays = n + (n-1) + (n-2) + (n-3) + . . . . . . + 3 + 2 + 1 = n(n+1)/2.

total = n(n + 1) / 2

Print the subarray of the array that starts from the start index and ends at the end index

Problem Statement

Given an array of integers and two indices, a start index and an end index, we need to print the subarrays of the array that starts from the start index and ends at the end index (both inclusive).

Solution

To solve this problem, we can simply iterate over the elements of the array from the start index to the end index (both inclusive) and print each element.

Pseudocode

void printSubarray(int arr[], int start, int end) {
    for (int i = start; i <= end; i++) {
        cout << arr[i] << " ";
    }
    cout << endl;
}

Time and Space Complexity

What will be T.C and S.C for the above approach?

Time Complexity : O(n)
Space Complexity : O(1)

Print all possible subarrays of the array

Problem Statement:

Given an array of integers, we need to print all possible subarrays of the array.

Example

Input: [1, 2, 3]
Output:
[1]
[1, 2]
[1, 2, 3]
[2]
[2, 3]
[3]

Solution

To solve this problem, we can generate all possible subarrays of the array using two nested loops.

• The outer loop iterates over the starting index of the subarray.
• The inner loop iterates over the ending index of the subarray.
• At each iteration, we print the subarray from the starting index to the ending index.

Pseudocode

void printSubarrays(int arr[], int n) {
    // Generate all possible subarrays
    for (int i = 0; i < n; i++) {
        for (int j = i; j < n; j++) {
            // Print the current subarray
            for (int k = i; k <= j; k++) {
                cout << arr[k] << " ";
            }
            cout << endl;
        }
    }
}

Time and Space Complexity

Time Complexity : O(N^3)
Space Complexity : O(1)

Problem 2 : Max And Min

Given an array of N integers, return the length of smallest subarray which contains both maximum and minimum element of the array.

Question

What is the length of the smallest subarray which has both, the max and the min of the array?

2	2	6	4	5	1	5	2	6	4	1

Choices

• 4
• 5
• 2
• 3

Here, minimum element is 1 and maximum is 6. Smallest subarray which contains both is from index 8 to index 10 which is of length 10-8+1=3.

Another Example

A[ ] = { 1, 2, 3, 1, 3, 4, 6, 4, 6, 3}
Ans = 4

Explanation:

Here, minimum element is 1 and maximum is 6. Smallest subarray which contains both is from index 3 to index 6 which is of length 6-3+1=4.

Warning

Please take some time to think about the brute force approach on your own before reading further.....

Problem 2 : Brute Force Solution

Check all subarrays and find the answer.

Time Complexity : O(N^3)
Space Complexity : O(1)

Note: It can be reduced to O(n^2) since we can check miniumum and maximum in a subarray in second loop itself.

Problem 2 : Optimised Solution Observation

• The answer subarray must have exactly one instance of minimum element and one instance of maximum element since we want the length to be minimum.
• The minimum and maximum value must be present at the corners of the subarray.
• So, basically we are looking for subarray which starts with maximum value and ends with closest minimum value or which starts with minimum value and ends with closest maximum value.

NOTE:

1. We can search a min for a max or vice versa, only in a single direction.
2. We don't have to consider all the pairs of min and max but look for closest pair, since we want to find smallest such subarray.
3. So we can keep track of the last found min and a last found max index.

Dry Run

A[ ] = { 2, 2, 6, 4, 5, 1, 5, 2, 6, 4, 1 }

Initially,
last_min_index = -1
last_max_index = -1
ans = INT_MAX
minValue = 1
maxValue = 6

i	A[i]	last_min_index	last_max_index	ans
0	2	-1	-1	INT_MAX
1	2	-1	-1	INT_MAX
2	6	-1	2	INT_MAX
3	4	-1	2	INT_MAX
4	5	-1	2	INT_MAX
5	1	5	2	5-2+1 = 4
6	5	5	2	4
7	2	5	2	4
8	6	5	8	4
9	4	5	8	4
10	1	10	8	10-8+1 = 3

So final ans would be 3.

Pseudocode

int minSubarray(int A[], int n) {
    // find maximum and minimum
    // values in the array
    int minValue = minOfArray(A);
    int maxValue = maxOfArray(A);

    int last_min_index = -1, last_max_index = -1, ans = INT_MAX;

    for (int i = 0; i < N; i++) {
        if (A[i] == minValue) {
            last_min_index = i;
            if (last_max_index != -1) {
                ans = min(ans, i - last_max_index + 1);
            }

        }
        if (A[i] == maxValue) {
            last_max_index = i;
            if (last_min_index != -1) {
                ans = min(ans, i - last_min_index + 1);
            }
        }
    }
    return ans;
}

Time and Space Complexity

What will be T.C and S.C for this approach?

Time Complexity : O(N)
Space Complexity : O(1)

---