Interview Problems¶

Analyzing constraints¶

Tips on Problem Constraints¶

Analyzing the constraints can help you determine which time complexity and data structure or algorithm to use for a given problem.
It is important to look at the constraints whenever we are solving a problem.

Note: In Interviews, don't ask the constraints directly. Rather, tell your approach and ask the interviewer if you need to optimize further.

If,

Constraint	Possible Time Complexities
n <= 10⁶	O(n), O(nlogn)
n <= 20	O(n!), O(2ⁿ)
n <= 10¹⁰	O(logn), O(sqrt(n))

Note: These are just general guidelines. The actual time complexity can vary based on the specific problem and implementation.

It's always important to analyze the problem and determine the best approach for your specific solution.

Problem 1 Find the maximum number of consecutive 1's after replacement¶

Problem Statement¶

Given an array of 1's and 0's, you are allowed to replace only one 0 with 1. Find the maximum number of consecutive 1's that can be obtained after making the replacement.

Example 1

Input = [1, 1, 0, 1, 1, 0, 1, 1]
Output = 5

Explanation:

If we replace 0 at 2^nd index or 0 at 5^th index with 1, in both cases we get 5 consecutes 1's.

Question¶

Find the maximum number of consecutive 1's that can be obtained after replacing only one 0 with 1.

A[] = [ 1, 1, 0, 1, 1, 0, 1, 1, 1 ]

Choices

4
5
6
7
If we replace 0 at 2^nd index with 1 we get 5 consecutes 1's.
If we replace 0 at 5^th index with 1 we get 6 consecutes 1's.

Hence, the maximum is 6 consecutive 1's.

Question¶

Find the maximum number of consecutive 1's that can be obtained after replacing only one 0 with 1.

A[] = [0, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0]

Choices

4
5
6
7
If we replace 0 at 0^th index with 1 we get 4 consecutes 1's.
If we replace 0 at 4^th index with 1 we get 6 consecutes 1's.
If we replace 0 at 7^th index with 1 we get 5 consecutes 1's.
If we replace 0 at last index with 1 we get 3 consecutes 1's.

Hence, the maximum is 6 consecutive 1's.

Warning

Please take some time to think about the solution approach on your own before reading further.....

Solution Approach¶

Maintain a variable say "ans", which keeps track of the maximum consecutive 1's encountered.
Initialize it with 0.
Iterate through the input array. When we encounter a zero at an index, we do the following:
- Count no. of consecutive 1's on left: l
- Count no. of consecutive 1's on right: r
- If (l+r+1 > ans), replace ans with (l+r+1).

Edge case: When all the array elements are 1's, then return the length of the whole array.

Pseudocode¶

int findMaxConsecutiveOnes(int nums[]) {
    int n = nums.size();
    int maxCount = 0;
    int totalOnes = 0;

    for (int i = 0; i < n; i++) {
        if (nums[i] == 1)
            totalOnes++;
    }

    if (totalOnes == n)
        return n;

    for (int i = 0; i < n; i++) {
        if (nums[i] == 0) {
            int l = 0, r = 0, j = i + 1;
            // calculate the maximum consecutive ones after replacing this zero
            while (j < n && nums[j] == 1) {
                r++;
                j++;
            }
            j = i - 1;
            while (j >= 0 && nums[j] == 1) {
                l++;
                j--;
            }
            maxCount = max(l + r + 1, count);
        }
    }

    return maxCount;
}

Question¶

What will be the TC of this approach ?

Choices

O(n)
O(n²)
O(n³)
O(n⁴)

Explanation:

The time complexity of the above solution is O(n) because it performs a single pass over the input array and every element will get accessed at maximum of 3 times.

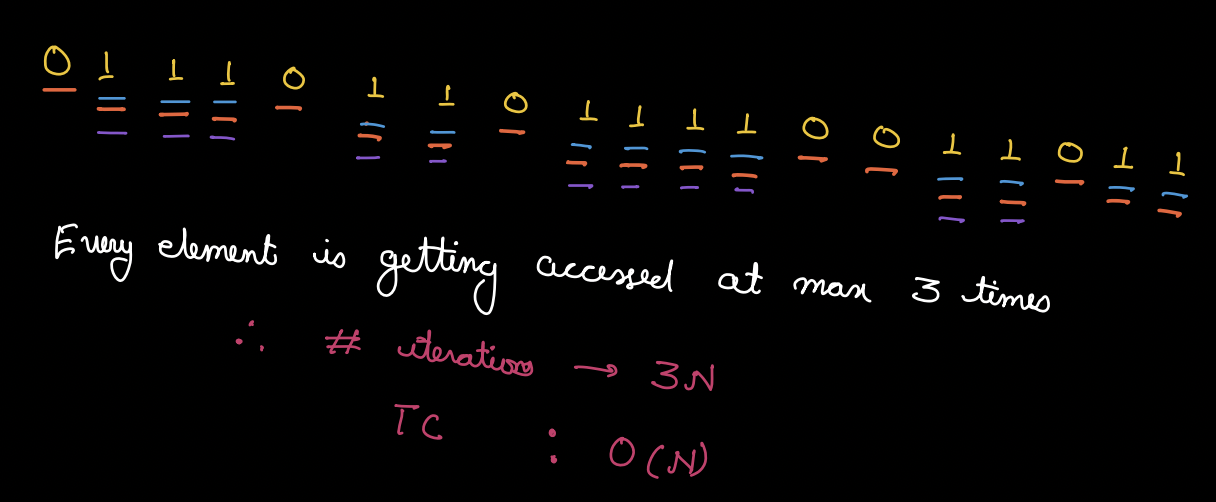
Variation of Problem 1¶

Coding Question 2¶

Problem Statement¶

Given an array of 1's and 0's, find the maximum number of consecutive 1's that can be obtained by SWAPPING at most one 0 with 1(already present in the string).

Example 1

Input: [1, 0, 1, 1, 0, 1]
Output: 5

Explanation:¶

We can swap zero at index 4 with 1 to get the array [1, 0, 1, 1, 1, 1], which has 5 consecutive 1s.

Question¶

find the maximum number of consecutive 1’s that can be obtained by swapping at most one 0 with 1.

A[] = [1, 1, 0, 1, 1, 1]

Choices

2
4
5
6

Explanation:

We can swap the zero at index 2 with 1 at either index 0 or index 5 to get the array which has 5 consecutive 1s.

Problem 1 variation continues¶

Solution¶

The solution is very similar to solution to previous problem except for some modifications.
We iterate through the input array. When we encounter a zero at an index, we do the following:
- Count no. of consecutive 1's on left -> l.
- Count no. of consecutive 1's on right -> r.
- If (l+r) is equal to total no. of 1's in the array, then currMax = (l+r), else currMax = (l+r+1).
- If (currMax > ans), replace ans with (currMax)

Edge case: When all the array elements are 1's, then return the length of the whole array.

Pseudocode¶

int findMaxConsecutiveOnes(int nums[]) {
    int n = nums.size();
    int maxCount = 0;
    int totalOnes = 0;

    for (int i = 0; i < n; i++) {
        if (nums[i] == 1)
            totalOnes++;
    }

    if (totalOnes == n)
        return n;

    for (int i = 0; i < n; i++) {
        if (nums[i] == 0) {
            int l = 0, r = 0, j = i + 1, currMax;
            // calculate the maximum consecutive ones after swapping this zero
            while (j < n && nums[j] == 1) {
                r++;
                j++;
            }
            j = i - 1;
            while (j >= 0 && nums[j] == 1) {
                l++;
                j--;
            }
            if (l + r == totalOnes)
                currMax = l + r;
            else
                currMax = l + r + 1
            maxCount = max(currMax, count);
        }
    }

    return maxCount;
}

Time and Space Complexity¶

Time Complexity : O(N)
Space Complexity : O(1)

Problem 2 Majority Element¶

Given an array of N integers, find the majority element.

The majority element is the element that occurs more than n/2 times where n is size of the array.

Example 1

A[ ] = { 2, 1, 4 }
Ans = No Majority element

Explanation¶

Here, none of the elements have frequency more than n/2 where n is 3.

Example 2

A[ ] = { 3, 4, 3, 2, 4, 4, 4, 4}
Ans = 4

Explanation¶

Here, frequency of 4 is more than n/2 that is 5 where n is 8. So 4 will be the majority element.

Example 3

A[ ] = { 3, 3, 4, 2, 4, 4, 2, 4}
Ans = No Majority element

Explanation:¶

Here, none of the elements have frequency more than n/2 where n is 8.

Question¶

What is the majority element in this array? 3, 4, 3, 6, 1, 3, 2, 5, 3, 3, 3

Choices

1
3
2
6

Here, 3 has frequency > n/2 where n is 11.

Question¶

What is the majority element in the following array?
4, 6, 5, 3, 4, 5, 6, 4, 4, 4

Choices

3
4
6
No Majority Element

Explanation:

Here, none of the elements have frequency more than n/2 where n is 10.

Question¶

At max how many majority elements can be there in an array?

Choices

1
2
n-1
n

Suppose there is an array of size n. If frequency of an element is greater than n/2, then there cannot exist an element in remaining elements whose frequency is greater than n/2 . Hence, there can be only one majority element.

Problem 2 Brute Force¶

Iterate through every element in the array, count the number of times each element appears, and return the element that appears more than n/2 times.

Pseudocode¶

void findMajority(int arr[], int n) {
    int maxCount = 0;
    int index = -1;
    for (int i = 0; i < n; i++) {
        int count = 0;
        for (int j = 0; j < n; j++) {
            if (arr[i] == arr[j])
                count++;
        }

        if (count > maxCount) {
            maxCount = count;
            index = i;
        }
    }

    if (maxCount > n / 2)
        print(arr[index])

    else
        print("No Majority Element")
}

Complexity¶

Time Complexity : O(N²)
Space Complexity : O(1)

Warning

Please take some time to think about the Optimised approach on your own before reading further.....

Problem 2 Optimised Approach using Moore’s Voting Algorithm¶

Observation 1:¶

There can only be one majority element in the array.

Proof:¶

We will prove it by contradiction.

Let's say there are two majority elements, say m1 and m2.
frequency(m1) > n/2 and frequency(m2) > n/2
Adding both sides,
- frequency(m1) + frequency(m2) > n [it not possible]
Hence, Prooved.

Observation 2:¶

If we remove any two distinct elements, the majority element remains the same.

Explanation 1:

Consider array of 13 blocks.

First 7 blocks are filled with GREEN colour.
Next 6 blocks are filled with RED colour.
Majority is GREEN.
If we remove 2 distinct blocks, 1 from GREEN and 1 from RED, we will be left with 11 elements.
Majority is still GREEN.

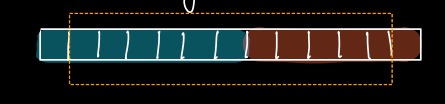
Again, If we remove 2 distinct elements, 1 from GREEN and 1 from RED, we will be left with 9 elements. Majority is still GREEN.

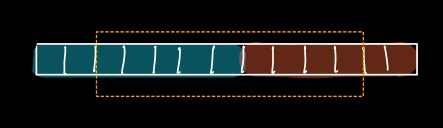
If we continue this process we will get GREEN as MAJORITY element.

Explanation 2:

Suppose there are 4 parties participating in an election.

First: ORANGE party(OP) with 9 candidates.
Second: YELLOW party(YP) with 3 candidates.
Third: RED party(RP) with 2 candidates.
Fourth: GREEN party(GP) with 3 candidates.

Currently, the WINNER is ORANGE

Remove	Orange	Yellow	Red	Green	Winner
1 OP and 1 YP	8	2	2	3	Orange
1 OP and 1 GP	7	2	2	2	Orange
1 OP and 1 RP	6	2	1	2	Orange
1 YP and 1 RP	6	1	0	2	Orange
1 YP and 1 GP	6	0	0	1	Orange
1 OP and 1 GP	5	0	0	0	Orange

We can observe that after removing 2 distinct party votes every time, majority is maintained at every point.

Note: We cannot remove same party votes twice.

Problem 2 Moore’s Voting Algorithm Approach and Dry Run¶

Approach¶

Iterate through each element of the array, keeping track of the majority element's count and index.
If the next element is the same as the current majority element, increase the count; otherwise, decrease the count.
If the count becomes zero, update the majority index to the current element and reset the count to 1.
After the iteration, go through the array once again and determine the count of the majority element found.
- If count > N/2, return majority elsement; else majority element doesn't exist.

Dry Run¶

Please dry run for the following example:

A[ ] = { 3, 4, 3, 6, 1, 3, 2, 5, 3, 3, 3 }

Pseudocode¶

int findCandidate(int a[], int size) {
    int maj_index = 0, count = 1;
    for (int i = 1; i < size; i++) {
        if (count == 0) {
            maj_index = i;
            count = 1;
        } else {
            if (a[maj_index] == a[i])
                count++;
            else
                count--;
        }
    }

    //check if the candidate
    //occurs more than n/2 times
    int count = 0;
    for (int i = 0; i < size; i++) {
        if (a[i] == a[maj_index])
            count++;
    }

    if (count > size / 2)
        return a[maj_index];

    else
        return -1;
}

Time and Space Complexity¶

What will be T.C and S.C for this approach?

Time Complexity : O(N)
Space Complexity : O(1)

Problem 3 Row to Column Zero¶

You are given a 2D integer matrix A, make all the elements in a row or column zero if the A[i][j] = 0. Specifically, make entire ith row and jth column zero.

Example

Input:

[1,2,3,4] [5,6,7,0] [9,2,0,4]

Output:

[1,2,0,0] [0,0,0,0] [0,0,0,0]

Explanation:

A[2][4] = A[3][3] = 0, so make 2^nd row, 3^rd row, 3^rd column and 4^th column zero

Observation¶

If you start row wise and make one row completely zero if it has 0 then you will loose information for making columns zero.

Note: None element is negative so see if you may use this for not loosing info.

Approach¶

Let's start row wise first.
Select rows one by one and make all the elements of that row -1(except which are 0), if any element in that row is 0.
Similariy you have to do the same thing for columns.
Now, before returning traverse the matrix and make all the -1 elements 0.

Pseudocode¶

int n = A.size(), m = A[0].size();
for (int i = 0; i < n; i++) {
    int flag = 0;
    for (int j = 0; j < m; j++) {
        if (A[i][j] == 0) flag = 1;
    }
    if (flag == 1) {
        for (int j = 0; j < m; j++) {
            if (A[i][j] != 0) A[i][j] = -1;
        }
    }
}
for (int j = 0; j < m; j++) {
    int flag = 0;
    for (int i = 0; i < n; i++) {
        if (A[i][j] == 0) flag = 1;
    }
    if (flag == 1) {
        for (int i = 0; i < n; i++) {
            if (A[i][j] != 0) A[i][j] = -1;
        }
    }
}
for (int i = 0; i < n; i++) {
    for (int j = 0; j < m; j++) {
        if (A[i][j] == -1) A[i][j] = 0;
    }
}
return A;