Introduction To Arrays¶

Space Complexity¶

Space complexity is the max space(worst case) that is utilised at any point in time during running the algorithm.
We also determine Space Complexity using Big O.

Consider the following example:

func(int N) { // 4 bytes
    int x; // 4 bytes
    int y; // 4 bytes
    long z; // 8 bytes
}

We only consider the space utilised by our program and not the Input Space since it is not in our control, hence we'll ignore space taken by "int N".
The above code takes total 16B of memory.
Hence, we say the Space Complexity of the above code is O(1) (1 resembles constant).

Question¶

Find the Space Complexity [Big(O)] of the below program.

func(int N) { // 4 bytes
    int arr[10]; // 40 Bytes
    int x; // 4 bytes
    int y; // 4 bytes
    long z; // 8 bytes
    int[] arr = new int[N]; // 4 * N bytes
}

Choices

N
4N + 60
Constant
N^2

Question¶

Find the Space Complexity [Big(O)] of the below program.

func(int N) { // 4 bytes
    int x = N; // 4 bytes
    int y = x * x; // 4 bytes
    long z = x + y; // 8 bytes
    int[] arr = new int[N]; // 4 * N bytes
    long[][] l = new long[N][N]; // 8 * N * N bytes
}

Choices

N
4N + 60
Constant
N^2

Question on Space Complexity¶

Find the Space Complexity [Big(O)] of the below program.

int maxArr(int arr[], int N) {
    int ans = arr[0];
    for(i from 1 to N-1) {
        ans = max(ans, arr[i]);
    }
    return ans;
}

Space complexity: O(1)¶

Don't consider the space acquired by the input size. Space complexity is the order of extra space used by the algorithm.
arr[] is already given to us, we didn't create it, hence it'll not be counted in the Space Complexity.
int N will also not be counted in space but since it is contant hence doesn't matter.
Additional space is also called computational or auxiliary space.
The above code finds the max element of the Array.

Introduction To Arrays¶

Definition¶

Array is the collection of same types of data. The datatype can be of any type i.e, int, float, char, etc. Below is the declaration of the array:

int arr[n];

Here, ‘int’ is the datatype, ‘arr’ is the name of the array and ‘n’ is the size of an array.
We can access all the elements of the array as arr[0], arr[1] ….. arr[n-1].

Note: Array indexing starts with 0.

Why indexing starts at 0 ?¶

An array arr[i] is interpreted as *(arr+i). Here, arr denotes the address of the first array element or the 0 index element. So *(arr+i) means the element at i distance from the first element of the array.

Question¶

What will be the indices of the first and last elements of an array of size N?

Choose the correct answer

Choices

1,N
0,N-1
1,N-1
0,N

Introduction to Arrays Continued¶

Print all elements of the array¶

The elements of arrays can be printed by simply traversing all the elements. Below is the pseudocode to print all elements of array.

void print_array(int arr[],int n){
    for(int i=0;i<n;i++){
        print(arr[i]);
    }
}

Question¶

What is the time complexity of accessing element at the ith index in an array of size N?

Choices

O(N)
O(1)
O(N*N)
O(log(N)).

Question¶

int arr[5] = {5,-4,8,9,10}
Print sum of 1^st and 5^th element
Choose the correct answer

Choices

print(arr[0]+arr[5])
print(arr[0]+arr[4])
print(arr[1]+arr[5])
print(arr[1]+arr[4])

Question 1 Reverse the array¶

Given an array 'arr' of size 'N'. Reverse the entire array.

TestCase:¶

Input:¶

N = 5
arr = {1,2,3,4,5}

Output:¶

arr = {5,4,3,2,1}

Warning

Please take some time to think about the solution approach on your own before reading further.....

Approach¶

The simplest approach to solve the problem is to keep two pointers at the end, traverse the array till middle element and swap first element with last element, second with second last, third with third last and so on.

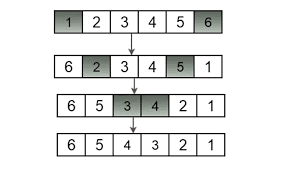
What should be the stopping condition?

Say N = 6

i	j	swap
0	5	A[0] & A[5]
1	4	A[1] & A[4]
2	3	A[2] & A[3]
3	2	STOP

Say N = 5

i	j	swap
0	4	A[0] & A[4]
1	3	A[1] & A[3]
2	2	STOP

We can stop as soon as i>=j

Pseudocode¶

Function reverse(int arr[], int N) {
  int i = 0, j = N - 1;
  while (i < j) {
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
    i++;
    j--;
  }
}

Complexity:¶

Time Complexity - O(N).
Space Complexity - O(1).

Question 2 Reverse in a range¶

Given an array 'arr' of size 'N' and integers 'l' and 'r'. Reverse the array from 'l' to 'r'.

TestCase:¶

Input:¶

N = 5
arr = {1,2,3,4,5}
[0 based index]
l = 1 
r = 3

Output:¶

arr = {1,4,3,2,5}

Pseudocode¶

Function reverse(int arr[], int N, int l, int r) {
    while (l < r) {
        int temp = arr[l];
        arr[l] = arr[r];
        arr[r] = temp;
        l++;
        r--;
    }
}

Complexity:¶

Time Complexity - O(N).
Space Complexity - O(1).

Question 3 Rotate K times¶

Given an array 'arr' of size 'N'. Rotate the array from right to left 'K' times. (i.e, if K = 1, last element will come at first position,...)

TestCase:¶

Input:¶

N = 5
arr = {1,2,3,4,5}
k = 2

Output:¶

arr = {4,5,1,2,3}

Explanation:¶

Initially the array is:

| 1 | 2 | 3 | 4 | 5 |

After 1^st rotation:

| 5 | 1 | 2 | 3 | 4 |

After 2^nd rotation:

| 4 | 5 | 1 | 2 | 3 |

Warning

Please take some time to think about the solution approach on your own before reading further.....

BruteForce Approach¶

Simple approach is to rotate the array one element at a time.

Pseudocode¶

Function rotateK(int arr[], int N, int K) {
    for (int i = 0; i < K; i++) {
        int temp = arr[N - 1];
        for (int j = N - 1; j >= 1; j--) {
            arr[j] = arr[j - 1];
        }
        arr[0] = temp;
    }
}

Complexity:¶

Time Complexity - O(N*K).
Space Complexity - O(1).

Optimized Approach¶

Success

Please take some time to think about the optimised solution approach on your own before reading further.....

Optimized Appraoch Observations¶

After K rotations, last K elements become 1^st K elements and rest elements will go at back.

For example - Suppose we have an array arr as shown below and k = 3.
1 2 3 4 5 6 7
After 1^st rotation, k=1:
7 1 2 3 4 5 6
After 2^nd rotation, k=2:
6 7 1 2 3 4 5
After 3^rd rotation, k=3:
5 6 7 1 2 3 4

So, we have observed that last 3(K=3) elements i.e, 5 6 7 comes in front and rest elements appear at the end.

Therefore, we will first reverse the entire array, then reverse first K elements individually and then next N-K elements individually.

1 2 3 4 5 6 7    //Given Array, K=3

7 6 5 4 3 2 1    //Reversed Entire Array

5 6 7 4 3 2 1    //Reversed first K elements

5 6 7 1 2 3 4    //Reversed last N-K elements

Pseudocode¶

Function countgreater(int arr[], int N, int k) {
    reverse(arr, N, 0, N - 1);
    reverse(arr, N, 0, K - 1);
    reverse(arr, N, K, N - 1);
}

Edge Case¶

K might be very large but if we observe carefully then after N rotations the array comes to its initial state.

Hence, K rotation is equivalent to K%N rotations.

Suppose we have an array:
1 2 3 4
After 1^st rotation, the array becomes:
2 3 4 1
After 2^nd rotation, the array becomes:
3 4 1 2
After 3^rd rotation, the array becomes:
4 1 2 3
Afer 4^th rotation, the array becomes:
1 2 3 4

Hence, we have concluded that after N rotations, the array become same as before 1^st rotation.

Final Pseudocode¶

Function countgreater(int arr[], int N, int K) {
    K = k % N;
    reverse(arr, N, 0, N - 1);
    reverse(arr, N, 0, K - 1);
    reverse(arr, N, K, N - 1);
}

Complexity:¶

Time Complexity - O(N).
Space Complexity - O(1).

Dynamic Arrays¶

Question:¶

What is the drawback of normal arrays?

Issue:¶

The size has to be declared before hand.

Dynamic Arrays¶

A dynamic array is an array with a big improvement: automatic resizing.
It expands as you add more elements. So you don't need to determine the size ahead of time.

Strengths:¶

Fast lookups: Just like arrays, retrieving the element at a given index takes O(1) time. Variable size: You can add as many items as you want, and the dynamic array will expand to hold them.

Weaknesses:¶

Slow worst-case appends:

Usually, adding a new element at the end of the dynamic array takes O(1) time.
But if the dynamic array doesn't have any room for the new item, it'll need to expand, which takes O(n) time.
- It is because we have to take a new array of bigger size and copy all the elements to a new array and then add a new element.
- So, Time Complexity to add a new element to Dynamic array is O(1) amortised.
Amortised means when most operations take O(1) but some operations take O(N).

Dynamic Arrays in Different Languages¶

Java¶

ArrayList<String> al = new ArrayList<>(); //Arraylist is created

al.add("50"); //50 is inserted at the end

al.clear(); // al={}

for (int i = 0; i < al.size(); i++) {
    System.out.print(al.get(i) + " ");
}                                        //iterating the Arraylist

C++¶

vector<int> a; //vector is created

a.push_back(60); 
//a = {10, 20, 30, 40, 50, 60} after insertion at end

a.clear(); // a={}

for(int i=0; i<a.size(); i++) {
    cout<<a[i];
}                             //iterating the vector

Python¶

thislist = [] //created list

thislist.append("orange") //added orange at end

thislist.clear()    //cleared the list

for i in range(len(thislist)):
  print(thislist[i])  //iterating on the list