Prefix Sum¶

Problem Description¶

Given N elements and Q queries. For each query, calculate sum of all elements from L to R [0 based index].

Example:¶

A[ ] = [-3, 6, 2, 4, 5, 2, 8, -9, 3, 1]

Queries (Q)

L	R	Solution
4	8	9
3	7	10
1	3	12
0	4	14
7	7	-9

Info

Before moving forward, think about the brute force solution approach.....

Brute Force Approach¶

For each query Q, we iterate and calculate the sum of elements from index L to R

Pseudocode¶

Function querySum(Queries[][], Array[], querySize, size) {
    for (i = 0; i < Queries.length; i++) {
        L = Queries[i][0]
        R = Queries[i][1]

        sum = 0
        for (j = L; j <= R; j++) {
            sum += Array[j]
        }
        print(sum)
    }
}

Time Complexity : O(N * Q)
Space Complexity : O(1)

Since Time complexity of this approach is O(N * Q) then in a case where there are 10^5 elements & 10^5 queries where each query is (L=0 and R=10^5-1) we would encounter TLE hence this approach is Inefficient

Question¶

Given the scores of the 10 overs of a cricket match 2, 8, 14, 29, 31, 49, 65, 79, 88, 97
How many runs were scored in just 7^th over?

Choices

16
20
18
17

Total runs scored in over 7^th : 65 - 49 = 16 (score[7]-score[6])

Question¶

Given the scores of the 10 overs of a cricket match 2, 8, 14, 29, 31, 49, 65, 79, 88, 97
How many runs were scored from 6^th to 10^th over(both included)?

Choices

66
72
68
90

Total runs scored in over 6^th to 10^th : 97 - 31 = 66 (score[10]-score[5])

Question¶

Given the scores of the 10 overs of a cricket match 2, 8, 14, 29, 31, 49, 65, 79, 88, 97
How many runs were scored in just 10^th over?

Choices

7
8
9
10

Total runs scored in over 6^th to 10^th : 97 - 88 = 9 (score[10]-score[9])

Question¶

Given the scores of the 10 overs of a cricket match< 2, 8, 14, 29, 31, 49, 65, 79, 88, 97
How many runs were scored from 3^rd to 6^th over(both included)?

Choices

70
40
9
41

Total runs scored in over 3^rd to 6^th : 49-8 = 41
(score[6]-score[2])

Question¶

Given the scores of the 10 overs of a cricket match 2, 8, 14, 29, 31, 49, 65, 79, 88, 97
How many runs were scored from 4^th to 9^th over(both included)?

Choices

75
80
74
10

Total runs scored in over 4^th to 9^th : 88 - 14 = 74 (score[9]-score[3])

Success

What do you observe from above cricket example ? Take some time and think about it....

Observation for Optimised Solution¶

Observation¶

On observing cricket board score, we can say that queries can be answered in just constant time since we have cummulative scores.
In the similar manner, if we have cummulative sum array for the above problem, we should be able to answer it in just constant time.
We need to create cumulative sum or prefix sum array for above problem.

How to create Prefix Sum Array ?¶

Definition¶

pf[i] = sum of all elements from 0 till ith index.

Example¶

Step1:-
Provided the intial array:-

2	5	-1	7	1

We'll create prefix sum array of size 5 i.e. size equal to intial array.
Initialise pf[0] = initialArray[0]

2	-	-	-	-

2	7	-	-	-

2	7	6	-	-

2	7	6	13	-

2	7	6	13	14

Finally we have the prefix sum array :-

2	7	6	13	14

Question¶

Calculate the prefix sum array for following array:-

10	32	6	12	20	1

Choices

[10,42,48,60,80,81]
[10,42,49,60,79,81]
[42,48,60,80,81,10]
[15,43,58,61,70,82]

Brute Force Code to create Prefix Sum Array and observation for Optimisation¶

pf[N]
for (i = 0; i < N; i++) {

    sum = 0;

    for (int j = 0; j <= i; j++) {
        sum = sum + A[j]
    }

    pf[i] = sum;
}

Observation for Optimising Prefix Sum array calculations¶

pf[0] = A[0]
pf[1] = A[0] + A[1]
pf[2] = A[0] + A[1] + A[2]
pf[3] = A[0] + A[1] + A[2] + A[3]
pf[4] = A[0] + A[1] + A[2] + A[3] + A[4]

Can we observe that we are making redundant calculations?
We could utilise the previous sum value.
- pf[0] = A[0]
- pf[1] = pf[0] + A[1]
- pf[2] = pf[1] + A[2]
- pf[3] = pf[2] + A[3]
- pf[4] = pf[3] + A[4]
Generalised Equation is: pf[i] = pf[i-1] + A[i]

Optimised Code:¶

pf[N]
pf[0] = A[0];
for (i = 1; i < N; i++) {
    pf[i] = pf[i - 1] + A[i];
}

Time Complexity: O(N)

How to answer the Queries ?¶

Success

Now that we have created prefix sum array...finally how can we answer the queries ? Let's think for a while...

A[ ] = [-3, 6, 2, 4, 5, 2, 8, -9, 3, 1]

pf[ ] =[-3, 3, 5, 9, 14, 16, 24, 15, 18, 19]

L	R	Solution
4	8	pf[8] - pf[3]	18 - 9 = 9
3	7	pf[7] - pf[2]	15 - 5 = 10
1	3	pf[3] - pf[0]	9 - (-3) = 12
0	4	pf[4]	14
7	7	pf[7] - pf[6]	15 - 24 = -9

Generalised Equation to find Sum:¶

sum[L R] = pf[R] - pf[L-1]

Note: if L==0, then sum[L R] = pf[R]

Complete code for finding sum of queries using Prefix Sum array:¶

Function querySum(Queries[][], Array[], querySize, size) {
    //calculate pf array
    pf[N]
    pf[0] = A[0];
    for (i = 1; i < N; i++) {
        pf[i] = pf[i - 1] + A[i];
    }

    //answer queries
    for (i = 0; i < Queries.length; i++) {
        L = Queries[i][0];
        R = Queries[i][1];

        if (L == 0) {
            sum = pf[R]
        } else {
            sum = pf[R] - pf[L - 1];
        }

        print(sum);
    }
}

Time Complexity : O(N+Q)
Space Complexity : O(N)

Space Complexity can be further optimised if you modify the given array.¶

Function prefixSumArrayInplace(Array[], size) {
    for (i = 1; i < size; i++) {
        Array[i] = Array[i - 1] + Array[i];
    }
}

Time Complexity : O(N)
Space Complexity : O(1)

Problem 1 : Sum of even indexed elements¶

Given an array of size N and Q queries with start (s) and end (e) index. For every query, return the sum of all even indexed elements from s to e.

Example

A[ ] = { 2, 3, 1, 6, 4, 5 }
Query :
 1 3
 2 5
 0 4
 3 3

Ans:
 1
 5
 7
 0

Explanation:¶

From index 1 to 3, sum: A[2] = 1
From index 2 to 5, sum: A[2]+A[4] = 5
From index 0 to 4, sum: A[0]+A[2]+A[4] = 7
From index 3 to 3, sum: 0

Brute Force¶

How many of you can solve it in O(N*Q) complexity?

Idea: For every query, Iterate over the array and generate the answer.

Warning

Please take some time to think about the Optimised approach on your own before reading further.....

Problem 1 : Observation for Optimisation¶

Whenever range sum query is present, we should think in direction of Prefix Sum.

Hint 1: Should we find prefix sum of entire array?

Expected: No, it should be only for even indexed elements.

We can assume that elements at odd indices are 0 and then create the prefix sum array.

Consider this example:-

  A[] = 2  3  1  6  4  5
PSe[] = 2  2  3  3  7  7

Note: PSe[i] denotes sum of all even indexed elements from 0 to ith index.

If i is even we will use the following equation :-

PSe[i] = PSe[i-1] + A[i]

If i is odd we will use the following equation :-

PSe[i] = PSe[i-1]

Question¶

Construct the Prefix Sum for even indexed elements for the given array [2, 4, 3, 1, 5]

Choices

1, 6, 9, 10, 15
2, 2, 5, 5, 10
0, 4, 4, 5, 5
0, 4, 7, 8, 8

We will assume elements at odd indices to be 0 and create a prefix sum array taking this assumption.

So 2 2 5 5 10 will be the answer.

Problem 1 : Pseudocode¶

void sum_of_even_indexed(int A[], int queries[][], int N) {
    // prefix sum for even indexed elements
    int PSe[N];

    if (A[0] % 2 == 0) PSe[0] = A[0];
    else PSe[0] = 0;

    for (int i = 0; i < N; i++) {
        if (i % 2 == 0) {
            PSe[i] = PSe[i - 1] + A[i];
        } else {
            PSe[i] = PSe[i - 1];
        }
    }
    for (int i = 0; i < queries.size(); i++) {
        s = queries[i][0]
        e = queries[i][1]
        if (s == 0) {
            print(PSe[e])
        } else {
            print(PSe[e] - PSe[s - 1])
        }
    }
}

Complexity¶

Time Complexity : O(N)
Space Complexity : O(N)

Problem 1 Extension : Sum of all odd indexed elements¶

If we have to calculate the sum of all ODD indexed elements from index s to e, then Prefix Sum array will be created as follows -

if i is odd PSo[i] = PSo[i-1] + array[i]

and if i is even :- PSo[i] = PSo[i-1]

Problem 2 : Special Index¶

Given an array of size N, count the number of special index in the array.

Note: Special Indices are those after removing which, sum of all EVEN indexed elements is equal to sum of all ODD indexed elements.

Example

A[ ] = { 4, 3, 2, 7, 6, -2 }
Ans = 2

We can see that after removing 0^th and 2^nd index S_e and S_o are equal.

i	A[i]	S_e	S_o
0	{ 3, 2, 7, 6, -2 }	8	8
1	{ 4, 2, 7, 6, -2 }	9	8
2	{ 4, 3, 7, 6, -2 }	9	9
3	{ 4, 3, 2, 6, -2 }	4	9
4	{ 4, 3, 2, 7, -2 }	4	10
5	{ 4, 3, 2, 7, 6 }	12	10

Note: Please keep a pen and paper with you for solving quizzes.

Question¶

What will be the sum of elements at ODD indices in the resulting array after removal of index 2 ?

A[ ] = [ 4, 1, 3, 7, 10 ]

Choices

8
14
11
9

After removal of element at index 2, elements after index 2 has changed their positions: Sum of elements at ODD indices from [0 to 1] + Sum of elements at EVEN indices from [3 to 4] = 1 + 10 = 11

Question¶

What will be the sum of elements at ODD indices in the resulting array after removal of index 3 ?

A[ ] = { 2, 3, 1, 4, 0, -1, 2, -2, 10, 8 }

Choices

8
15
12
21

Explanation:

After removal of element at index 3, elements after index 3 has changed their positions: Sum of elements at ODD indices from [0 to 2] index + Sum of elements at EVEN indices from [4 to 9] = A[1]+A[4]+A[6]+A[8] = 3+0+2+10 = 15

Question¶

What will be the sum of elements at EVEN indices in the resulting array after removal of index 3 ?

[2, 3, 1, 4, 0, -1, 2, -2, 10, 8]

Choices

15
8
10
12

After removal of element at index 3, elements are after index 3 has changed their positions: Sum of elements at EVEN indices from [0 to 2] index + Sum of elements at ODD indices from [4 to 9] = A[0]+A[2]+A[5]+A[7]+A[9] = 2+1+(-1)+(-2)+8 = 8

Warning

Please take some time to think about the optimised solution approach on your own before reading further.....

Problem 2 : Observation for Optimised Approach¶

Suppose, we want to check if i is a Special Index.
Indices of elements present on the left side of i will remain intact while indices of elements present on the right side of element i will get changed.
Elements which were placed on odd indices will shift on even indices and vice versa.

For example:

A[ ] = { 2, 3, 1, 4, 0, -1, 2, -2, 10, 8 }

Sum of ODD indexed elements after removing element at index 3 =

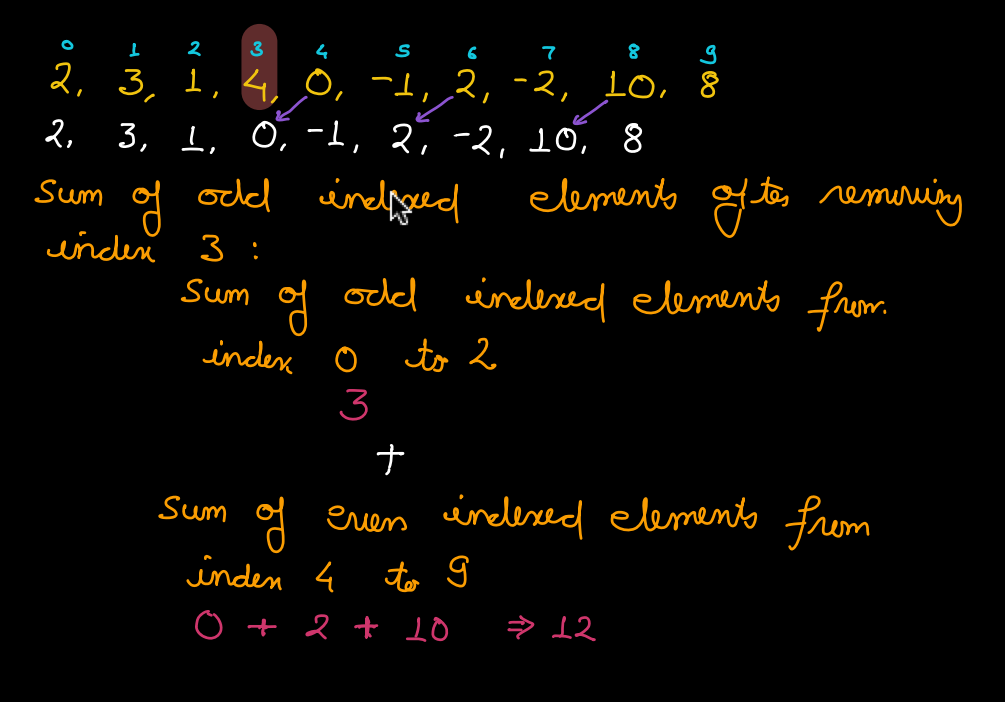
Sum of EVEN indexed elements after removing element at index 3 =

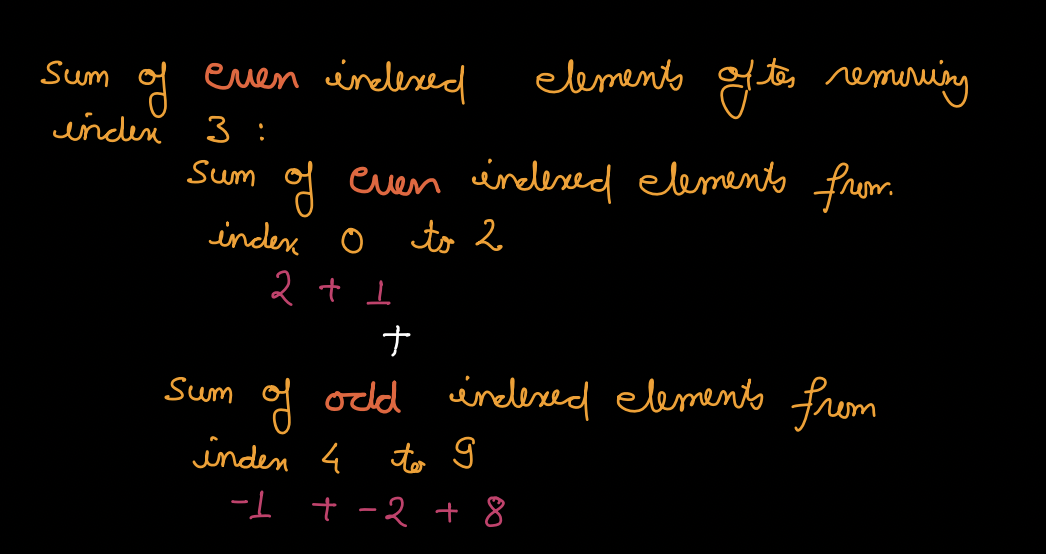
Approach¶

Create Prefix Sum arrays for ODD and EVEN indexed elements.
Run a loop for i from 0 to n – 1, where n is the size of the array.
For every element check whether So is equal to Se or not using the above equations.
Increment the count if Se is equal to So.

NOTE: Handle the case of i=0.

Pseudocode¶

int count_special_index(int arr[], int n) {
    // prefix sum for even indexed elements
    int PSe[n];
    // prefix sum for odd indexed elements
    int PSo[n];

    //Say we have already calculated PSe and PSo

    //Code to find Special Indices

    int count = 0;
    for (int i = 0; i < n; i++) {

        int Se, So;

        if (i == 0) {
            Se = PSo[n - 1] - PSo[i]; //sum from [i+1 n-1]
            So = PSe[n - 1] - PSe[i]; //sum from [i+1 n-1]
        } else {
            Se = PSe[i - 1] + PSo[n - 1] - PSo[i]; //sum even from [0 to i-1] and odd from [i+1 n-1]
            So = PSo[i - 1] + PSe[n - 1] - PSe[i]; //sum odd from [0 to i] and even from [i+1 n-1]           
        }
        if (Se == So) {
            count++;
        }
    }
    return count;
}

Complexity¶

Time Complexity : O(N)
Space Complexity : O(N)