Introduction to Problem Solving¶

Notes Description¶

Introduction to Problem Solving
Time Complexity
Introduction to Arrays
Prefix Sum
Carry Forward
Subarrays
2D Matrices
Sorting Basics
Hashing Basics
Strings Basics
Bit Manipulation Basics
Interview Problems

Following will be covered in the notes!

Count the Factors
Optimisation for counting the Factors
Check if a number is Prime
Sum of N Natural Numbers
Definition of AP & GP
How to find the number of a times a piece of code runs, i.e, number of Iterations.
How to compare two Algorithms.

Count of factors of a number N¶

Q. What is a factor?

A. We say i is a factor of N if i divides N completely, i.e the remainder is 0.

How to programmatically check if i is a factor of N ?

We can use % operator which gives us the remainder.

=> N % i == 0

Question 1:

Given N, we have to count the factors of N.

Note: N > 0

Question 2:

Number of factors of the number 24.

Choices

4
6
8
10

Explanation:

1, 2, 3, 4, 6, 8, 12, and 24 are the factors.

Question 3:

Number of factors of the number 10.

Choices

1
2
3
4

Explanation:

1, 2, 5, and 10 are the factors.

Warning

Please take some time to think about the solution approach on your own before reading further.....

Counting Factors Brute force solution¶

What is the minimum factor of a number ?

=> 1

What is the maximum factor of a number ?

=> The number itself

So, we can find all factors of N from 1 to N.

Pseudocode¶

function countfactors (N):
    fac_count = 0
    for i = 1 till N:
        if N % i == 0:
            fac = fac + 1

    return fac

Observations for Optimised Solution¶

Now, your code runs on servers.
When you submit your code, do you expect some time within which it should return the Output ?
You wouldn't want to wait when you even don't know how long to wait for ?
Just like that one friend who says, 'Just a little more time, almost there.' And you feel annoyed, not knowing how much longer you'll have to wait.

Servers have the capability of running ~10^8 Iterations in 1 sec.

N	Iterations	Execution Time
10^8	10^8 iterations	1 sec
10^9	10^9 iterations	10 sec
10^18	10^18 iterations	317 years

Optimisation for Counting Factors¶

Optimization:

i * j = N -> {i and j are factors of N}

=> j = N / i -> {i and N / i are factors of N}

For example, N = 24

i	N / i
1	24
2	12
3	8
4	6
6	4
8	3
12	2
24	1

Q. Can we relate these values?

A. We are repeating numbers after a particular point. Here, that point is from 5^th row.

Now, repeat the above process again for N = 100.

i	N / i
1	100
2	50
4	25
5	20
10	10
20	5
25	4
50	2
100	1

Warning

Please take some time to think about the solution approach on your own before reading further.....

The factors are repeating from 6^th row. After a certain point factors start repeating, so we need to find a point till we have to iterate.

We need to only iterate till -

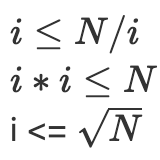
Pseudocode¶

function countfactors (N):
    fac_count = 0
    for i = 1 till sqrt(N):
        if N % i == 0:
            fac = fac + 2

    return fac

Q. Will the above work in all the cases? A. No, not for perfect squares. Explain this for N = 100, what mistake we are doing. We will count 10 twice.

Observation: Using the above example, we need to modify the code for perfect squares.

Pseudocode with Edge Case Covered¶

function countfactors (N):
    fac_count = 0
    for i = 1 till sqrt(N):
        if N % i == 0:
            if i == N / i:
                fac = fac + 1
            else:
                fac = fac + 2

    return fac

Dry run the above code for below examples, N = 24, 100, 1.

N	Iterations	Execution Time
10^18	10^9 iterations	10 secs

To implement sqrt(n) , replace the condition i <= sqrt(N) by i * i <= N.

Follow Up Question¶

Given N, You need to check if it is prime or not.

Question

How many prime numbers are there?

10, 11, 23, 2, 25, 27, 31

Choices

1
2
3
4

Explanation:

Q. What is a prime Number?

A. Number which has only 2 factors, 1 and N itself.

So, 11, 23, 2, and 31 are the only prime numbers since they all have exactly 2 factors.

Prime Check¶

Our original question was to check if a number is prime or not. For that, we can just count the number of factors to be 2.

function checkPrime(N):
    if countfactors(N) == 2:
        return true
    else:
        return false

For N = 1, it will return false, which is correct. Since, 1 is neither prime nor composite.

Question

1 + 2 + 3 + 4 + 5 + 6 + .. 100 = ?

Choices

1010
5050
5100
1009

Explanation:

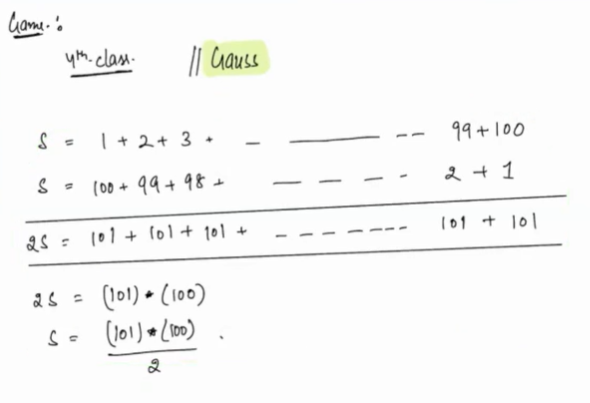
Generalize this for the first N natural numbers.

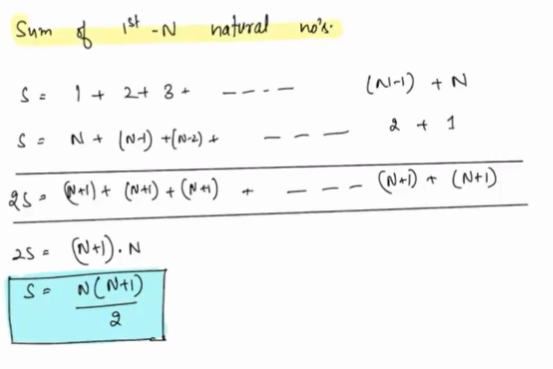
Some basic math properties:¶

[a,b] - This type of range means that a and b are both inclusive.
(a,b) - This type of range means that a and b are both excluded.

Question

How many numbers are there in the range [3,10]?

Choices

7
6
8
10

Explanation:

The range [3,10] includes all numbers from 3 to 10, inclusive. Inclusive means that both the lower bound (3) and the upper bound (10) are included in the range. Thus the numbers that are included are 3 4 5 6 7 8 9 10.

Question

How many numbers are there in the range [a,b]?

Choices

b-a
b-a+1
b-a-1

Explanation:

To find the number of numbers in a given range, we can subtract the lower bound from the upper bound and then add 1. Mathematically, this can be expressed as:

Number of numbers in the range 
= Upper bound - Lower bound + 1

What do we mean by Iteration?¶

The number of times a loop runs, is known as Iteration.

Question

How many times will the below loop run ?

for(i=1; i<=N; i++)
{
    if(i == N) break; 
}

Choices

N - 1
N
N + 1
log(N)

Question

How many iterations will be there in this loop ?

for(int i = 0; i <= 100; i++){
    s = s + i + i^2;
}

Choices

100 - 1
100
101
0

Question

How many iterations will be there in this loop?

func(){
    for(int i = 1; i <= N; i++){
        if(i % 2 == 0){
            print(i);
        }
    }
    for(int j = 1; j <= M; j++){
        if(j % 2 == 0){
            print(j);
        }
    }
}

Choices

N
M
N * M
N + M

Explanation:

We are executing loops one after the other. Let's say we buy first 5 apples and then we buy 7 apples, the total apples will be 12, so correct ans is N + M

Geometric Progression (G.P.)¶

Example for intution:

5 10 20 40 80 ..

In these type of series, the common ratio is same. In the given example the common ratio r is

= 10/5
= 20/10
= 40/20
= 80/40
= 2

Generic Notation:

a, a * r, a * r^2, ...

Sum of first N terms of a GP¶

Sum of first N terms of GP:

r cannot be equal to 1 because the denominator cannot be zero.

Note:

When r is equal to 1, the sum is given by a * n.

How to compare two algorithms?¶

Story

There was a contest going on to SORT the array and 2 people took part in it (say Gaurav and Shila).

They had to sort the array in ascending order.

arr[5] = {3, 2, 6, 8, 1} -> {1, 2, 3, 6, 8}

Both of them submitted their algorithms and they are being run on the same input.

Discussion¶

Can we use execution time to compare two algorithms?

Say initially Algo1 took 15 sec and Algo2 took 10sec.

This implies that Shila's Algo 1 performed better, but then Gaurav pointed out that he was using Windows XP whereas Shila was using MAC, hence both were given the same laptops.........

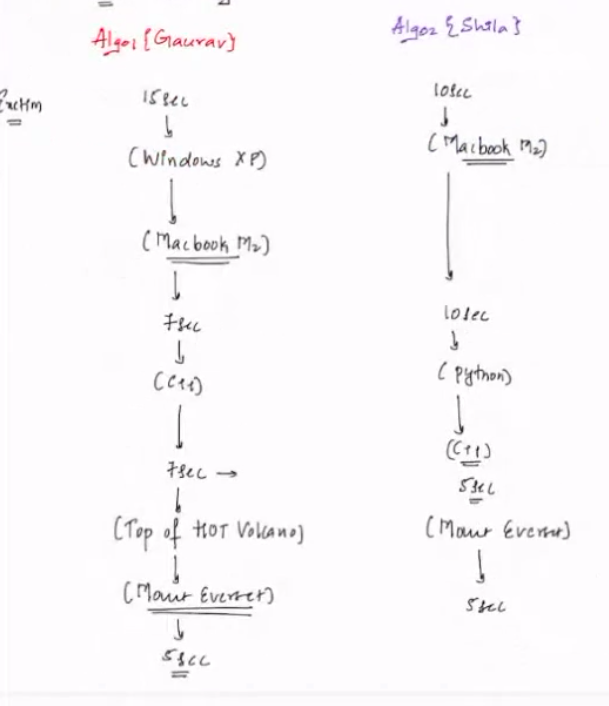
Conclusion¶

We can't evaluate algorithm's performance using execution time as it depends on a lot of factors like operating system, place of execution, language, etc.

Question How can we compare two algorithms?

Which measure doesn't depend on any factor?

Answer: Number of Iterations

Why?

The number of iterations of an algorithm remains the same irrespective of Operating System, place of execution, language, etc.