Sorting

Introduction

Sorting is an arrangement of data in particular order on the basis of some parameter

Example 1:

 A[ ] = { 2, 3, 9, 12, 17, 19 }

The above example is sorted in ascending order on the basis of magnitude.

Example 2:

 A[ ] = { 19, 6, 5, 2, -1, -19 }

The above example is sorted in descending order on the basis of magnitude.

Question

Is the array { 1, 13, 9 , 6, 12 } sorted ?

Choices

• Yes
• No

In the above quiz, array is sorted in ascending order on the basis of count of factors. Count of factors for the above array is { 1, 2, 3, 4, 6 }.

Sorting is essential for organizing, analyzing, searching, and presenting data efficiently and effectively in various applications and contexts.

Problem 1 : Minimize the cost to empty array

Given an array of n integers, minimize the cost to empty given array where cost of removing an element is equal to sum of all elements left in an array.

Example 1

A[ ] = { 2, 1, 4 }
Ans = 11

Explanation

After removing 4 cost = 4+2+1 = 7
After removing 2 cost = 2+1 = 3
After removing 1 cost = 1 = 1

Total cost = 11

Question

Minimum cost to remove all elements from array {4, 6, 1} ?

Choices

• 11
• 15
• 17
• 21

After removing 6 cost = 4+6+1 = 11
After removing 4 cost = 4+1 = 5
After removing 1 cost = 1 = 1

Total cost = 17

Question

Minimum cost to remove all elements from array[] = {3, 5, 1, -3}

Choices

• 4
• 2
• 0
• 18

After removing 5 cost = 5+3+1+(-3) = 6
After removing 3 cost = 3+1+(-3) = 1
After removing 1 cost = 1+(-3) = -2
After removing -3 cost = -3) = -3

Total cost = 2

Warning

Please take some time to think about the solution approach on your own before reading further.....

Problem 1 Solution Approach

Observation

• Start removing from the largest element.

Here we can see if we have to minimise the cost we should add the largest number minimum number of times, that implies it should be the first one to be removed.

The formula would be sum(i+1)*arr[i] where i is the index.

Follow the below steps to solve the problem.

• Sort the data in descending order.
• Initialise the ans equal to 0.
• Run a loop for i from 0 to n – 1, where n is the size of the array.
• For every element add arr[i]*i to the ans.

Pseudocode

int calculate_cost(int arr[], int n) {
    reverse_sort(arr);
    int ans = 0;
    for (int i = 0; i < n; i++) {
        ans += i * arr[i];
    }

    return ans;
}

Time and Space Complexity

Time Complexity: O(NLogN).
Space Complextiy: O(N).

Problem 2 : Find count of Noble Integers

Given an array of distinct elements of size n, find the count of noble integers.

Note: arr[i] is noble if count of elements smaller than arr[i] is equal to arr[i] where arr[i] is element at index i.

Example 1

A[ ] = { 1, -5, 3, 5, -10, 4}
Ans = 3

Explanation

For arr[2] there are three elements less than 3 that is 1, -5 and -10. So arr[0] is noble integer.
For arr[3] there are five elements less than 5 that is 1, 3, 4, 5, -5 and -10. So arr[3] is noble integer.
For arr[5] there are four elements less than 4 that is 1, 3, -5 and -10. So arr[5] is noble integer.

In total there are 3 noble elements.

Question

Count the number of noble integers in the array. A = { -3, 0, 2 , 5 }

Choices

• 0
• 1
• 2
• 3

Explanation:

For arr[2] there are two elements less than 2 that is -3 and 0. So arr[2] is noble integer. In total there are 2 noble elements.

Warning

Please take some time to think about the Brute Force solution approach on your own before reading further.....

Problem 2 : Bruteforce Solution

Observation

Iterate through every element in the array, for every element count the number of smaller elements.

Pseudocode

int find_nobel_integers(int arr[], int n) {
    int ans = 0;
    for (int i = 0; i < n; i++) {
        int count = 0;
        for (int j = 0; j < n; j++) {
            if (arr[j] < arr[i])
                count++;
        }
        if (count == arr[i]) {
            ans++;
        }
    }
    return ans;
}

Time and Space Complexity

Time Complexity: O(N^2).
Space Complextiy: O(1).

Problem 1 Optimised Solution

Optimised Solution - 1

• Hint 1: What is the extra work being done? Expected: For every element, we are using an extra loop for calculating the count of smaller elements.
• Hint 2: Can sorting the array help here?

Observation:

If we sort the data all elements smaller than the element at index i will be on from index 0 to i-1. So total number of smaller elements will be equal to i.

Pseudocode

int find_nobel_integers(int arr[], int n) {
    sort(arr);
    int ans = 0;
    for (int i = 0; i < n; i++) {
        if (arr[i] == i) {
            ans = ans + 1;
        }
    }
    return ans;
}

Time and Space Complexity

Time Complexity: O(NLogN).
Space Complextiy: O(1).

Problem 3 Find count of nobel integers (Not Distinct)

Given an array of size n, find the count of noble integers.

Note: Same as previous question, but all elements need not to be distinct

Question

Count the no of noble integers in the array. A = { -10, 1, 1, 3, 100 }

Choices

• 1
• 3
• 2
• 4

Explanation:

For arr[1] and arr[2] there is one element less than 1. So arr[1] and arr[2] are noble integers.
Similarly arr[3] will be the npble lement as there are 3 elements less than 3. So in total 3 elements are noble integers.

Question

Count the no of noble integers in the array
A = { -10, 1, 1, 2, 4, 4, 4, 8, 10 }

Choices

• 4
• 5
• 6
• 7

Explanation:

arr[1], arr[2], arr[4], arr[5], arr[6] are the noble elements here.

Question

Count the no of noble integers in the array
A = { -3, 0, 2, 2, 5, 5, 5, 5, 8, 8, 10, 10, 10, 14 }

Choices

• 4
• 5
• 6
• 7

Explanation:

For arr[8] and arr[9] there are eight elements less than 8 that is -3, 0, 2, 5. So arr[8] and arr[9] are noble integers.
Similarly arr[9], arr[10], arr[11], ar[12] are noble elements.
So in total 6 elements are noble integers.

Warning

Please take some time to think about the solution approach on your own before reading further.....

Problem 3 Solution

Observation

• If the current element is same as previous element then the total number of smaller elements will be same as previous element.
• If current element is not equal to previous element then the total number of smaller elements is equal to its index.

Pseudocode

int find_nobel_integers(int arr[], int n) {
    sort(arr);
    int count = 0, ans = 0;
    if (arr[0] == 0) ans++;

    for (int i = 1; i < n; i++) {
        if (arr[i] != arr[i - 1])
            count = i;

        if (count == arr[i])
            ans++;
    }
    return ans;
}

Time and Space Complexity

Time Complexity: O(NLogN).
Space Complextiy: O(1).

Sorting Algorithm - Selection Sort

A sorting algorithm is a method of reorganizing the elements in a meaningful order.

Imagine this. You are asked to arrange students according to their increasing heights.

Divide the queue of students into two parts – arranged and unarranged.

1. To begin with, place all the students in the unarranged queue.
2. From this unarranged queue, search for the shortest student and place him/her in the list of arranged students.
3. Again, from the unarranged queue, select the second-shortest student. Place this student in the arranged queue, just after the smallest student.
4. Repeat the above-given steps until all the students are placed into the arranged queue.

Did you see what we just did here?

We used the selection sort algorithm to arrange all the students in a height-wise order.

To better understand selection sort, let's consider a list of Integers 5, 6, 4, 2.

The steps to sort this list would involve –

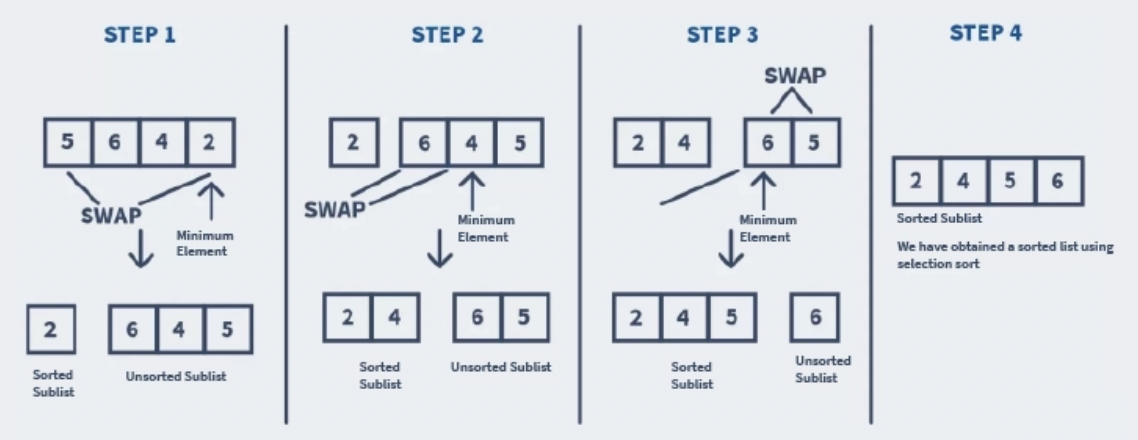
Pseudocode:

void selectionSort(int arr[], int size) {
    int i, j, minIndex;

    for (i = 0; i < size - 1; i++) {

        // set minIndex equal to the first unsorted element
        minIndex = i;

        //iterate over unsorted sublist and find the minimum element
        for (j = i + 1; j < size; j++) {

            if (arr[j] < arr[minIndex]) {
                minIndex = j;
            }

        }

        // swapping the minimum element with the element at minIndex to place it at its correct position 
        swap(arr[minIndex], arr[i]);
    }
}

TC & SC

Time Complexity:

O(N²) since we have to iterate entire list to search for a minimum element everytime.
For 1 element, N iterations,
For N elements, N² iterations.

Space Complexity: O(1)

Sorting Algorithm - Insertion Sort

Insertion Sort is one of the simplest sorting techniques which you might have used in your daily lives while arranging a deck of cards.

So without going into how this algorithm works, let’s think about how you would usually go about arranging the deck of cards?

Say you are given 10 cards, 1 to 10 of spades, all shuffled, and you want to sort these cards.

1. You would basically pick any random card(e.g. 7), and place it into your left hand, assuming the left hand is meant to carry the sorted cards.
2. Then you would pick another random card, say 2, and place 2 in the correct position on your left hand, i.e. before 7.
3. Then again if you pick 5, you would place it between 2 and 7 on your left hand, and this way we know we are able to sort our deck of cards. Since we insert one element at a time in its correct position, hence its name “Insertion Sort”.

Dry Run

E.g. if elements were in order:

3, 5, 2

You can start by picking 3, and since there is no element to the left of 3, we can assume it is in the correct place.

Array:

3, 5, 2

You can pick 5, you compare 5 with 3, and you find 5 is in the correct order amongst the array of [3, 5].

Array:

3, 5, 2

Then you pick 2, you find the place in the left side array of [3,5] to place this 2. Since 2 must come before 3, we insert 2 before 3.

Array:

2, 3, 5 →

Which is a sorted order.

Approach

Line 2: We don’t process the first element, as it has nothing to compare against.
Line 3: Loop from i=1 till the end, to process each element.
Line 4: Extract the element at position i i.e. array[i]. Let it be called E.
Line 5: To compare E with its left elements, loop j from i-1 to 0
Line 6, 7: Compare E with the left element, if E is lesser, then move array[j] to right by 1.
Line 8: Once we have found the position for E, place it there.

Pseudocode

void insertionSort(int arr[], int n) {
    for (int i = 1; i < n; i++) { // Start from 1 as arr[0] is always sorted
        Int currentElement = arr[i];
        Int j = i - 1;
        // Move elements of arr[0..i-1], that are greater than key,
        // to one position ahead of their current position
        while (j >= 0 && arr[j] > currentElement) {
            arr[j + 1] = arr[j];
            j = j - 1;
        }
        // Finally place the Current element at its correct position.
        arr[j + 1] = currentElement;
    }
}

TC & SC

Time Complexity:

Worst Case: O(N^2), when the array is sorted in reverse order.

Best Case: O(N), when the data is already sorted in desied order, in that case there will be no swap.

Space Complexity: O(1)

Note

1. Both Selection & Insertion are in-place sorting algorithms, means they don't need extra space.
2. Since the time complexity of both can go to O(N^2), it is only useful when we have a lesser number of elements to sort in an array.

---