Sliding Window & Contribution Technique¶

Problem 1 : Find the max sum out of all possible subarray of the array¶

Problem Statement¶

Given an array of integers, find the total sum of all possible subarrays. #Note: This question has been previously asked in Google and Facebook.

Solution¶

We can use the previous approach, where we calculated all sum subarray using Carry Forward technique.
Instead of keeping track of maximum, we can simply add the sums in a variable.

Pseudocode¶

int sumOfAllSubarraySums(int arr[], int n) {
    int total_sum = 0;
    for (int i = 0; i < n; i++) {
        int subarray_sum = 0;
        for (int j = i; j < n; j++) {
            subarray_sum += arr[j];
            total_sum += subarray_sum;
        }
    }
    return total_sum;
}

Time and Space Complexity¶

Time Complexity : O(N^2)
Space Complexity : O(1)

Problem 2 : Contribution Technique¶

We can optimize the above solution further by observing a pattern in the subarray sums. Let's take the example array [1, 2, 3]. The subarrays and their sums are:

[1] -> 1
[1, 2] -> 3
[1, 2, 3] -> 6
[2] -> 2
[2, 3] -> 5
[3] -> 3
Total Sum = 1+3+6+2+5+3 = 20

Instead of generating all subarrays, we can check that a particular element appears in how many subarrays and add its contribution that many times to the answer.

the first element 1 appears in 3 subarrays: [1], [1, 2], and [1, 2, 3].
the second element 2 appears in 4 subarrays: [2], [1, 2], [2, 3], and [1, 2, 3].
the third element 3 appears in 3 subarrays: [3], [2, 3], and [1, 2, 3].

Total = \((1*3) + (2*4) + (3*3) = 20\)

Warning

Please take some time to think about "How to calculate the number of subarrays in which A[i] appears?" on your own before reading further.....

Question¶

In how many subarrays, the element at index 1 will be present? A: [3, -2, 4, -1, 2, 6 ]

Choices

6
3
10
8

Explanation:

The subarrays in which the element at index 1 is present are -

[3, -2], [3, -2, 4], [3, -2, 4, -1], [3, -2, 4, -1, 2], [3, -2, 4, -1, 2, 6], [-2], [-2, 4], [-2, 4, -1], [-2, 4, -1, 2], [-2, 4, -1, 2, 6 ]. There are total 10 such subarrays.

Question¶

In how many subarrays, the element at index 2 will be present?

A: [3, -2, 4, -1, 2, 6 ]

Choices

6
12
10
8

Explanation:

The subarrays in which the element at index 1 is present are -

[3, -2, 4], [3, -2, 4, -1], [3, -2, 4, -1, 2], [3, -2, 4, -1, 2, 6], [-2, 4], [-2, 4, -1], [-2, 4, -1, 2], [-2, 4, -1, 2, 6], [4], [4, -1], [4, -1, 2], [4, -1, 2, 6 ]. There are total 12 such subarrays.

Find sum of all Subarrays sums continued¶

Generalized Calculation -

The start of such subarrays can be 0, 1, ..I

The end of such subarrays can be i, i+1, i+2, ...n-1

Elements in range [0 i] = i+1

Elements in range [i n-1] = n-1-i+1 = n-i

Thus, the total number of subarrays containing arr[i] is i+1 multiplied by n-i.

This gives us the expression (i+1) * (n-i).

We can use this pattern to compute the total sum of all subarrays in O(n) time complexity.

The steps are as follows:

Initialize a variable total_sum to zero.
Iterate over all elements of the input array arr. For each element arr[i], compute arr[i] * (i+1) * (n-i) and add it to total_sum.
Return total_sum as the output of the function.

Pseudocode¶

int sumOfAllSubarraySums(arr[]) {
    int n = arr.size();
    int total_sum = 0;

    // Iterate over all elements of the array and compute the sum of all subarrays containing that element
    for (int i = 0; i < n; i++) {
        total_sum += arr[i] * (i + 1) * (n - i);
    }

    return total_sum;
}

Time and Space Complexity¶

Time Complexity : O(N)
Space Complexity : O(1)

Total number of subarrays of length K¶

Number of subarrays of length K = Total number of start indices of subarrays of length K.

length (K)	start of first window	start of last window
1	0	N-1
2	0	N-2
3	0	N-3
4	0	N-4
K	0	N-K

All start positions for length K, will be within range [0 N-K]. Therefore total is N-K+1.

Hence, total number of subarrays of length K = N-K+1.

Question¶

Given N=7, K=4, what will be the total number of subarrays of len K?

Choices

3
4
5
6

Problem 3 Given an array, print start and end indices of subarrays of length K.¶

Given an array of size N, print start and end indices of subarrays of length K.

Example

If N=8, K=3
All start and end indices are

start	end
0	2
1	3
2	4
3	5
4	6
5	7

[start end] = K
end - start + 1 = K
end = K + start - 1

Pseudocode¶

```cpp= //Iterate over all the start indices for (int i = 0; i <= N - K; i++) { int j = K + i - 1;

print(i, j);

} ```

Note: Now we know how to iterate over windows of length K.

Problem 4 : Given an array, print maximum subarray sum with length K¶

Given an array of N elements. Print maximum subarray sum for subarrays with length = K. Example N=10 K=5 | -3 | 4 | -2 | 5 | 3 | -2 | 8 | 2 | -1 | 4 | | --- | --- | --- | --- | --- | --- | --- | --- | --- |:---:| Explanation | s | e | sum | | -------- | -------- | -------- | | 0 | 4 | 7 | | 1 | 5 | 8 | | 2 | 6 | 12 | | 3 | 7 | 16 | | 4 | 8 | 10 | | 5 | 9 | 11 | Maximum: 16

Warning

Please take some time to think about the solution approach on your own before reading further.....

Problem 4 : Bruteforce Approach¶

We have to calculate the sum of all subarrays of size k and find the maximum out of them

Pseudeocode¶

cpp function maxSubarrayOfLengthK(A[], N, K) { ans = INT_MIN //first window i = 0 j = k - 1 while (j < N) { sum = 0 for (idx = start; idx <= end; idx++) { sum += A[idx] } ans = max(sum, ans) //going to next subarray of length k i++ j++ } print(ans) }

Complexity¶

For what value of k will the iterations be highest ?

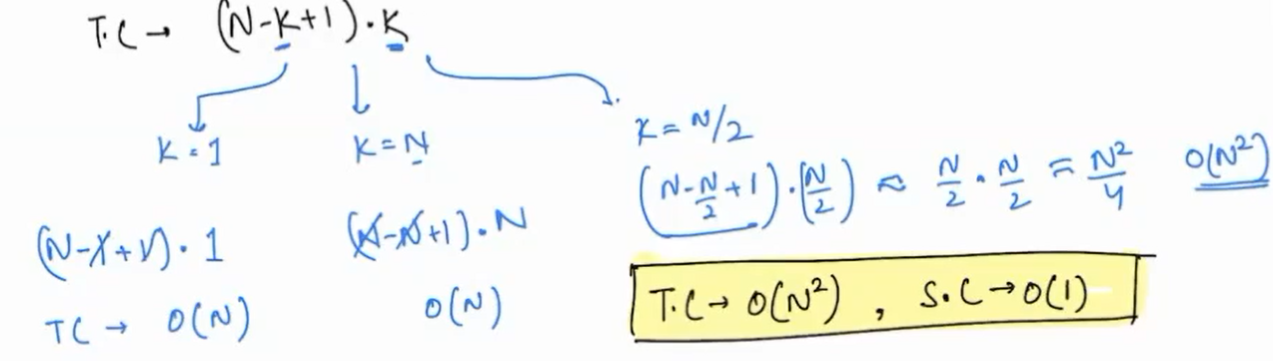
Warning

Please take some time to think about the optimised solution approach on your own before reading further.....

Problem 4 : Optimized Approach using Prefix Sum Array¶

We can use Prefix Sum Array since we have to find sum within a range.

Pseudeocode¶

function maxSubarrayOfLengthK(A[], N, K) {
    // calculate prefix sum array
    pf[N]
    pf[0] = A[0]
    for (idx = 1; idx < N; idx++) {
        pf[idx] = pf[idx - 1] + A[idx];
    }
    ans = INT_MIN
    i = 0
    j = K - 1
    // calculate for each pair of indicies   
    while (j < N) {
        sum = pf[j] - (i == 0 ? 0 : pf[i - 1])

        ans = max(sum, ans)
        i++
        j++
    }
    print(ans)

}

Question¶

What is Time Complexity and Space Complexity respectively?

Choices

O(N^2) and O(N)
O(N) and O(N)
O(N) and O(N^2)
O(1) and O(N)

Problem 4 Optimized Approach : using Sliding Window¶

We want to reduce the space complexity without modifying the given array, but how?

Observations¶

We can get sum of next subarray using current subarray sum as follows:-
- By adding a new element to current sum.
- By subtracting the first element of current subarray.

Given array :-

-3	4	-2	5	3	-2	8	2	-1	4

First subarray from 0 to 4:-

-3	4	-2	5	3

Converting first to second subarray :-

-3	4	-2	5	3	-2

Based upon above observation can we say:-

Warning

sum of all elements of next subarray = sum of elements of current subarray - first element of current subarray + new element

This approach is known as Sliding window approach.

Dry Run¶

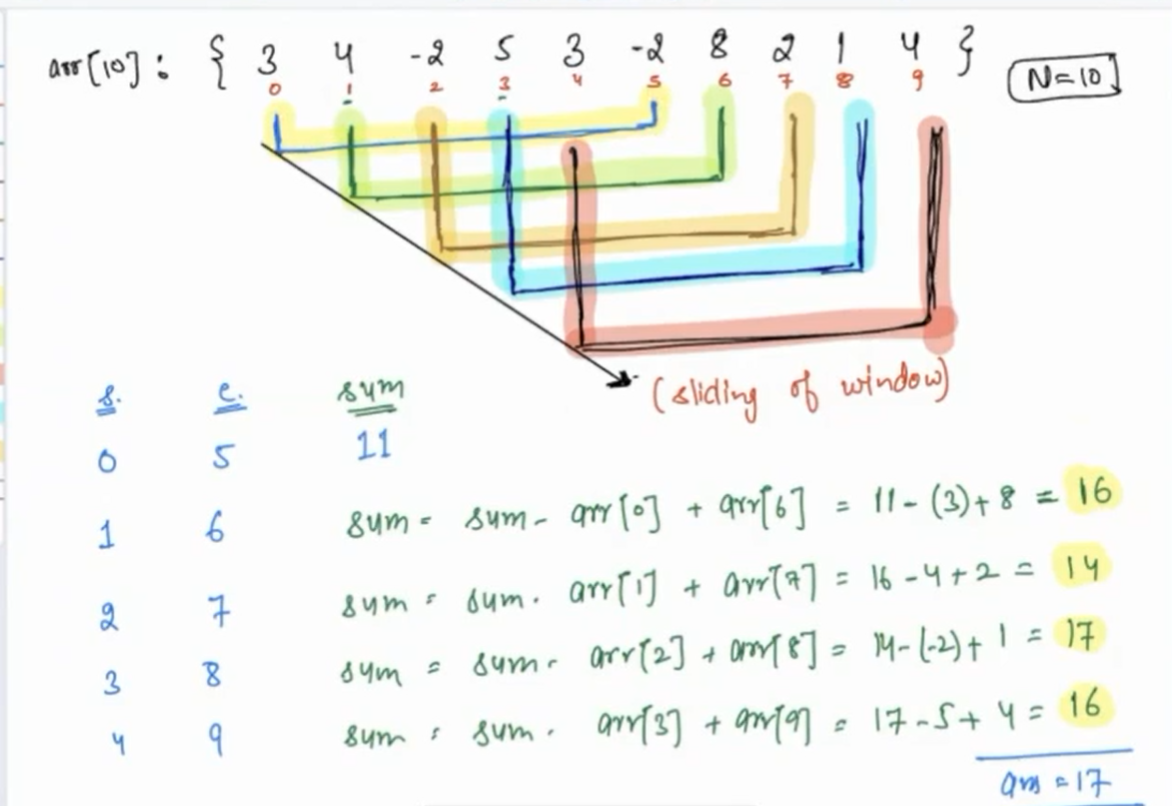
We can clearly observe the window sliding in above run.

Pseudeocode¶

function maxSubarrayOfLengthK(A[], N, K) {
    ans = INT_MIN
    i = 0
    j = K - 1

    sum = 0 // here k iterations
    for (int idx = i; idx <= j; idx++) {
        sum += A[idx]
    }
    ans = max(sum, ans)

    j++
    i++

    while (j < N) {
        sum = sum + A[j] - A[i - 1]

        ans = max(sum, ans)
        // here N-k iterations
        i++
        j++
    }
    print(ans)

}

Time Complexity : O(N)
Space Complexity : O(1)

Observations for solving problems on Subarrays.¶

Observations¶

Following are the observations that can be useful when solving problems related to subarrays:

Subarrays can be visualized as contiguous part of an array, where the starting and ending indices determine the subarray.
The total number of subarrays in an array of length n is n*(n+1)/2.
To print all possible subarrays, O(n^3) time complexity is required.
The sum of all subarrays can be computed in O(n^2) time complexity and O(1) space complexity by using Carry Forward technique.
The sum of all subarrays can be computed in O(n^2) time complexity and O(n) space complexity using the prefix sum technique.
The number of subarrays containing a particular element arr[i] can be computed in O(n) time complexity and O(1) space complexity using the formula (i+1)*(n-i). This method is called Contribution Technique.