Time Complexity¶

Topics covered :

Log Basics + Iteration Problems
Comparing Iterations using Graph
Time Complexity - Definition and Notations (Asymptotic Analysis - Big O)
TLE
Importance of Constraints

Success

There are a lot of quizzes in this session, please take some time to think about the solution on your own before reading further.....

Basics of Logarithm¶

Q. What is the meaning of LOG ?

A. Logarithm is the inverse of exponential function.

Q. How to read the statement "log_b(a)"?

A. To what value we need to raise b, such that we get a.

If log_b(a) = c, then it means b^c = a.

Examples

log₂(64) = 6
How? 2 raise to the power what is 64? It's 6 since 2⁶ = 64
log₃(27) = 3
log₅(25) = 2
log₂(32) = 5

Now, calculate the floor values of the following logarithms.

log₂(10) = 3
log₂(40) = 5

Note: If 2^k = N => log₂(N) = k

Let's look at one more formula:

What is log₂(2^6)?

A. 6 Explanation: To what power you should raise 2, such that it equates to 2^6.

What is log₃(3^5)?

A. 5

Explanation: To what power you should raise 3, such that it equates to 3^5.

Note:

In general, log_a(a^N) = N

Question:

Given a positive integer N, how many times do we need to divide it by 2 (Consider only integer part) until it reaches 1.

For example, N = 100 100 -> 50 -> 25 -> 12 -> 6 -> 3 -> 1 Hence, 6 times.

What if N = 324? 324 -> 162 -> 81 -> 40 -> 20 -> 10 -> 5 -> 2 -> 1 Hence, 8 times.

Question¶

How many times we need to divide 9 by 2 till it reaches 1 ?

Choices

4
3
5
2

Explanation:

N → N/2 → N/4 → N/8 → ...... 1
N/2^0 → N/2^1 → N/2^2 → N/2^3 → ...... N/2^K

N/2^K = 1
K = log₂(N)

Question¶

How many times we need to divide 27 by 2 till reaches 1 ?

Choices

5
4
3
6

Question¶

How many iterations will be there in this loop ?

N > 0
i = N;
while (i > 1) {
    i = i / 2;
}

Choices

N
N/2
sqrt(N)
log(N)

Explanation:

The given loop starts with the initial value of i as N and continues until i becomes less than or equal to 1, by repeatedly dividing i by 2 in each iteration.

Hence, Iterations are log(N)

Question¶

How many iterations will be there in this loop

for(i=1; i<N; i=i*2)
{ 
    ...
}

Choices

infinite
sqrt(N)
0
log(N)

Question¶

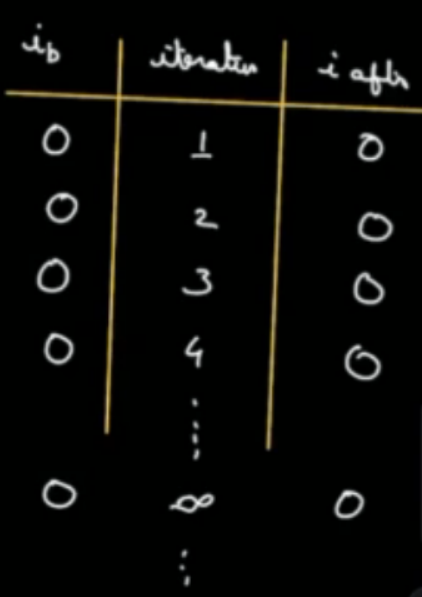
How many iterations will be there in this loop ?

N>=0
for(i=0; i<=N; i = i*2)
{ 
    ...
}

Choices

Infinite
N/2
0
log(N)

Question¶

How many iterations will be there in this loop

for(i=1; i<=10; i++){
    for(j=1; j<=N; j++){
    /     ......../
    }
}

Choices

N + N
N^2
10 * N
N + 10

Multiplying the loops each time might not be correct. In this case, it works.

Question¶

How many iterations will be there in this loop

for(i=1; i<=N; i++){
    for(j=1; j<=N; j++){
        ...
    }
}

Choices

2 * N
N * N
10 * N
N * sqrt(N)

Explanation:

The given loop consists of two nested loops. The outer loop iterates from i=1 to i=N, and the inner loop iterates from j=1 to j=N.

For each value of i in the outer loop, the inner loop will iterate N times. This means that for every single iteration of the outer loop, the inner loop will iterate N times.

Therefore, the correct answer is N * N.

Question¶

How many iterations will be there in this loop

for(i=1; i <= N; i++){
    for(j=1; j <= N; j = j*2){ 
        ... 
    }
}

Choices

(N^2 + 2N + 1)/2
N * log(N)
N^2
N(N+1)/2

Explanation:

The given loop consists of two nested loops. The outer loop iterates from i=1 to i <= N, and the inner loop iterates from j=1 to j <= N, with j being incremented by a power of 2 in each iteration.

For each value of i in the outer loop, the inner loop iterates in powers of 2 for j. This means that the inner loop will iterate for j=1, 2, 4, 8,... up to the largest power of 2 less than or equal to N, which is log₂(N).

Therefore, the correct answer is N * log₂(N).

Question¶

How many iterations will be there in this loop ?

for(i = 1; i <= 4; i++) {
    for(j = 1; j <= i ; j++) {
        //print(i+j)
    }
}

Choices

log(N)
2N
10
N →

Question¶

How many Iterations will be there in this loop ?

for(i = 1; i <= N; i++) {
    for(j = 1; j <= i ; j++) {
        //print(i+j)
    }
}

Choices

log(N)
N*(N+1)/2
(N-1)/2
N/2

Question¶

How many iterations will be there in this loop

for(i=1; i<=N; i++){
    for(j=1; j<=(2^i); j++)
    { 
        ...
    }
}

Choices

2^N
2 * (2^N - 1)
2 * (2N)
infinite

This is GP, where a=2, r=2 and no. of terms are N.

Consider two algorithms Algo1 and Algo2 given by Kushal and Ishani respectively.

Considering N to be the size of the input:

Algo	Number of Iterations
Algo1	100 * log(N)
Algo2	N / 10

Now, see the graph of the two algorithms based on N.

Graphs info:

X-axis plots N (input size)
Red line (Algo 1): 100 * log(N)
Blue line (Algo 2): N/10

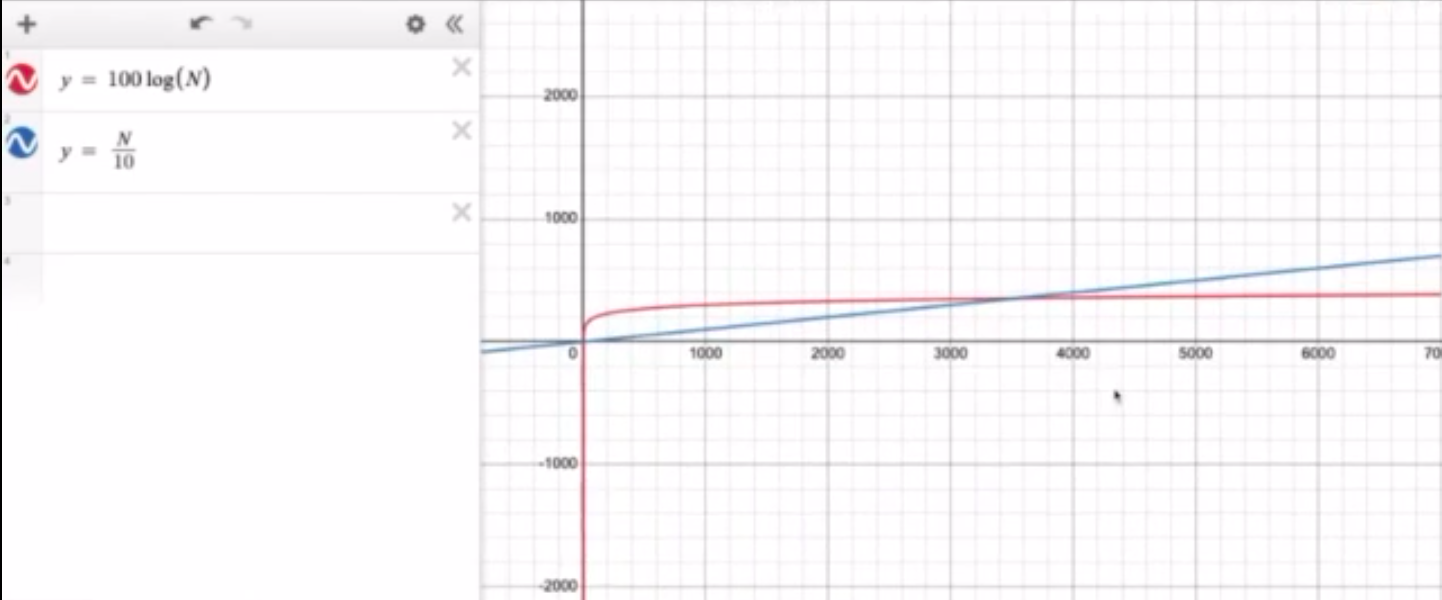
Observations:¶

Assuming both graphs intersect at N = 3500, let's draw some observations.

For small input (N <= 3500), Ishani's algorithm performed better.

For large input (N > 3500), Kushal's algorithm performed better.

In today's world data is huge

IndiaVSPak match viewership was 18M.
Baby Shark video has 2.8B views.

Therefore, Kushal's algorithm won since it has lesser iterations for huge data value.

We use Asymptotic Analysis to estimate the performance of an Algorithm when Input is huge.

Asymptotic Analysis OR Big(O) simply means analysing perfomance of algorithms for larger inputs.

Calculation of Big(O)¶

Steps for Big O calculation are as follows:

Calculate Iterations based on Input Size
Ignore Lower Order Terms
Ignore Constant Coefficients

Example-

Kushal's algo took 100 * log₂N iterations: Big O is O(log₂N)
Ishani's algo took N / 10 iterations: Big O is O(N)

For example,

Iterations: 4N^2 + 3N + 1
Neglect lower order term: 3N + 1; Remaining Term: 4N^2
Neglect constant 4

Big O is O(N^2)

Comparsion Order:¶

log(N) < sqrt(N) < N < N log(N) < N sqrt(N) < N^2 < N^3 < 2^(N) < N! < N^N

Using an example

N = 36
5 < 6 < 36 < 36*5 < 36*6 < 36² < 36³ < 2³⁶ < 36! < 36³⁶

Ques: What is the big notation time complexity of the following expression?

4N^2 + 3N + 6 sqrt(N) + 9 log_2(N) + 10
Ans = O(N^2)

Question¶

F(N) = 4N + 3Nlog(N) + 1
O(F(N)) = ?

Choices

N
N * logN
Constant
N^2

Question¶

F(N) = 4NlogN + 3NSqrt(N) + 10^6
O(F(N)) = ?

Choices

N
N * logN
N^2
N * Sqrt(N)

Why do we neglect Lower Order Terms¶

Let's say the number of Iterations of an Algorithm are: N²+10N

N	Total Iterations = N²+10N	Lower Order Term = 10N	% of 10N in total iterations = 10N/(N²+10N)*100
10	200	100	50%
100	10⁴+10³	10³	Close to 9%
10000	10⁸+10⁵	10⁵	0.1%

Conclusion¶

We can say that, as the Input Size increases, the contribution of Lower Order Terms decreases.

Why do we neglect Constant Coefficients¶

When the comparison is on very larger input sizes, the constants do not matter after a certain point. For example,

Algo 1(Nikhil)	Algo 2(Pooja)	Winner for Larger Input
10 * log₂ N	N	Nikhil
100 * log₂ N	N	Nikhil
9 * N	N²	Nikhil
10 * N	N² / 10	Nikhil
N * log₂ N	100 * N	Pooja

Issues with Big(O)¶

Issue 1¶

We cannot always say that one algorithm will always be better than the other algorithm.

Example:

Algo1 (Iterations: 10³ N) -> Big O: O(N)
Algo2 (Iterations: N²) -> Big O: O(N²)
Algo 1 is better than Algo 2 but only for large inputs, not for small input sizes.

Input Size (N)	Algo 1 (10³)	Algo 2 (N²)	Optimised
N = 10	10⁴	10²	Algo 2
N = 100	10⁵	10⁴	Algo 2
N = 10³	10⁶	10⁶	Both are same
N = 10³ + 1	(10³)*(10³ + 1)	(10³ + 1)*(10³ + 1)	Algo 1
N = 10⁴	10⁷	10⁸	Algo 1

Claim: For all large inputs >= 1000, Algo 1 will perform better than Algo 2.

Issue 2¶

If 2 algorithms have same higher order terms, then Big O is not capable to identify algorithm with higher iterations.

Consider the following questions -

Count the number of odd elements from 1 to N

Code 1: Iterations: N

for (int i = 1; i <= N; i++) {
    if (i % 2 != 0) {
        c = c + 1;
    }
}

Code 2: Iterations: N/2

for (int i = 1; i <= N; i = i + 2) {
    c = c + 1;
}

In both, Big O is O(N) but we know second code is better.

Time Limit Exceeded Error¶

Is it necessary to write the entire code and then test it to determine its correctness?
Can we assess the logic's viability before writing any code?

Online Editors and Why TLE occurs¶

Codes are executed on online servers of various platforms such as Codechef, Codeforces, etc.
The processing speed of their server machines is 1 GHz which means they can perform 10⁹ instructions per second.
Generally, codes should be executed in 1 second.

Using this information, we can say at max our code should have at most 10⁹ instructions.

Instructions means any single operation such as multiplication, addition, function calling, single variable declaration, etc.

Question¶

Consider the following code:

Find the total number of instructions in the code below (Note that the instructions involved in the loop part are repetitive)

Conclusion:

Calculating Instructions is tedious job, rather we can make certain approximations in terms of number of Iterations.

Approximation 1¶

Suppose the code has as small as 10 Instructions in 1 Iteration.

Therefore,

Instructions	Iterations
10	1
10^9	10^8

In 1 sec, we can have at max 10⁹ Instructions or 10⁸ Iterations, provided there are 10 Instructions / Iteration.

Approximation 2¶

Suppose the code has as huge as 100 Instructions in 1 Iteration.

Therefore,

Instructions	Iterations
100	1
10^9	10^7

In 1 sec, we can have at max 10⁹ Instructions or 10⁷ Iterations, provided there are 100 Instructions / Iteration.

Conclusion:¶

In general, our code can have 10⁷ to 10⁸ Iterations to be able to run in 1 sec.

General Structure to solve a question¶

How to approach a problem?¶

Read the Question and Constraints carefully.
Formulate an Idea or Logic.
Verify the Correctness of the Logic.
Mentally develop a Pseudocode or rough Idea of Loops.
Determine the Time Complexity based on the Pseudocode.
Assess if the time complexity is feasible and won't result in Time Limit Exceeded (TLE) errors.
Re-evaluate the Idea/Logic if the time constraints are not met; otherwise, proceed.
Code the idea if it is deemed feasible.

Importance of Constraints¶

Question¶

If 1 <= N <= 10⁵,
then which of the following Big O will work ?

Complexity	Iterations	Works ?
O(N³)	(10⁵)³	No
O(N²) log N	(10¹⁰)*log 10⁵	No
O(N²)	(10⁵)²	No
O(N * log N)	(10⁵)*log 10⁵	Yes

Question¶

If 1 <= N <= 10⁶,
then which of the following Big O will work ?

Complexity	Iterations	Works ?
O(N³)	(10⁶)³	No
O(N²) log N	(10¹²)*log 10⁶	No
O(N²)	(10¹²)	No
O(N * log N)	(10⁶)*log 10⁶ ~ 10⁷	May Be
O(N)	(10⁶)	Yes

Question¶

If constraints are
1 <= N <= 100, N³ will also pass.

If constraints are
1 <= N <= 20, 2^N will also pass.

Note: In Online Assessments, if we are not getting any other approach to a problem, try out the code; it may pass some test cases, which is better than nothing.