Maths Basics and Calculate Iterations¶
Agenda of this Lecture:¶
- Maths Basics
- GCD
- LCM
- Iteration Calculation
Let us learn some basic maths concepts, starting with Sum of natural numbers.
Question¶
Sum of first N natural numbers =
Choices¶
- N*(N + 1)
- N*(N + 1) / 2
- N*(N - 1)
- N*(N - 1) / 2
Explanation¶
The sum of the first N natural numbers is equal to \(N(N+1)/2\). For example, the sum of the first 6 natural numbers is \(6(6+1)/2 =42/2= 21\)
Question¶
How many numbers are there in this range [3,10] ? both corners included
Choices¶
- 7
- 8
- 9
- 10
Explanation:
The numbers in this range are: 3, 4, 5, 6, 7, 8, 9, and 10. Therefore, there are 8 numbers in the range [3, 10] (both corners included).
Question¶
How many numbers are there from [a b] both included
Choices¶
- b - a
- b - a + 1
- b - a - 1
- None of them
Explanation:¶
If we have a range [a, b] where both endpoints are included, we can calculate the number of numbers in that range by taking the absolute difference between b and a and adding 1.
Question¶
How many numbers are there in this range [4,7] ? both corners included
Choices¶
- 2
- 3
- 4
- 5
Explanation:¶
If we apply the formula here ie b - a + 1, here b = 7, a = 4. Hence b - a + 1 = 4.
Point to remember:-
- Elements in range [a,b). In this a is included but b is excluded.
- Elements in range (a,b). In this both a and b are excluded.
Geometric Progression(GP)¶
Definition A sequence of numbers is called a Geometric progression (GP) if the ratio of any two consecutive terms is always the same.
Example 1:
2 6 18 54 162
The sequence 2, 6, 18, 54, 162 is a GP because ratio of any two consecutive terms in the series (common difference) is same
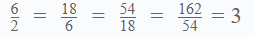
Example 2:
3 6 12 24 48 96
The sequence 3, 6, 12, 24, 48, 96 is a GP because ratio of any two consecutive terms in the series is same(ie 2).
Explanation
In simple terms, A geometric series is a list of numbers where each number, or term, is found by multiplying the previous term by a common ratio r. The formula for the sum of the nth term of Geometric Progression:
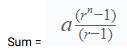
Where,
Sum = Sum of all Geometric Progressions n= number of terms r = Common ratio
Example
Given series: 2,4,8,16,32
Sum of first five terms in this series will be given by:
a = 2 , r = 2, n = 5
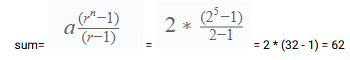
Break Statement¶
To stop the iterations of a loop before it actually completes, we use the break statement.
Question¶
What is the output of the following code?
for(int i = 1; i <= 5; i ++ ) {
SOPln(i);
}
Choices¶
- 1 2 3 4 5
- 1 2 3 4
- 1 2
- None of the above
Question¶
What is the output of the following code?
for(int i = 1; i <= 5; i ++ ) {
SOPln(i);
if (i == 3) {
break;
}
}
Choices¶
- 1 2 3
- 1 2 3 4
- 1 2
- None of the above
Question¶
What is the output of the following code?
for(int i = 1; i <= 5; i ++ ) {
SOPln(i);
if (i == 3) {
break;
}
}
Choices¶
- 1 2 3
- 1 2 3 4
- 1 2
- None of the above
Dry Run:

Question¶
What is the output of the following code?
for(int i = 1; i <= 5; i ++ ) {
if (i == 3) {
break;
}
SOPln(i);
}
Choices¶
- 1 2
- 1 2 3 4
- 1 2 4 5
- None of the above
Dry Run

Explain break statement in case of nested loops.
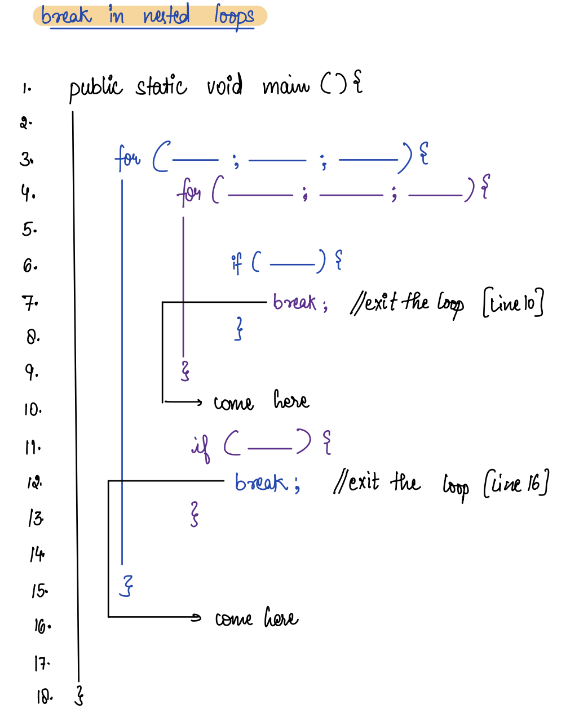
Given two numbers A and B, find their GCD.
Note: GCD of A and B means the greatest positive integer that divides both A and B.
Examples:
A = 24
B = 36
Factors of A = 1, 2, 3, 4, 6, 8, 12, 24
Factors of B = 1, 2, 3, 4, 6, 9, 12, 18, 36
Common Factors: 1, 2, 3, 4, 6, 12
GCD = 12
A = 5
B = 10
Factors of A = 1, 5
Factors of B = 1, 2, 5, 10
Common Factors: 1, 5
GCD = 5
A = 12
B = 18
Factors of A = 1, 2, 3, 4, 6, 12
Factors of B = 1, 2, 3, 6, 9, 18
Common Factors: 1, 2, 3, 6
GCD = 6
Take more examples if required.
Using examples, explain the following observations:
Observation 1¶
Minimum number that can possibly divide A and B = 1. Maximum number that can possibly divide A and B = MIN(A, B).
Observation 2¶
The GCD lies in the range of 1 to MIN(A, B).
Idea 1¶
Check all possible candidates from 1 to MIN(A, B).

Code:
int A = scn.nextInt();
int B = scn.nextInt();
int min = 0;
if (A < B) {
min = A;
}
else min = B;
int gcd = 0;
for(int i = 1; i <= min; i ++ ) {
if (A % i == 0 && B % i == 0) {
gcd = i;
}
}
SOPln(gcd);
Show dry run with A = 8, B = 6.
Question¶
What is the HCF/GCD of 7 and 12?
Choices¶
- 1
- 2
- 7
- None of the above
Question¶
What is the HCF/GCD of 10 and 15?
Choices¶
- 10
- 1
- 3
- 5
Idea 2 for Calculating GCD¶
Go from MIN(A, B) to 1 and whenever you find first factor of both A and B, break and print that factor.
Dry run for A=10 and B=15
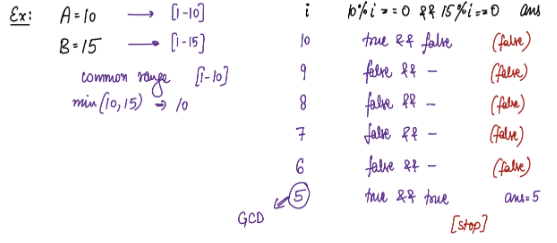
Show examples.
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int a = sc.nextInt();
int b = sc.nextInt();
int min = 0;
if(a < b){
min = a;
}
else{
min = b;
}
int gcd = 0;
for (int i = min; i >= 1; i -- ) {
if (a % i == 0 && b % i == 0) {
gcd = i;
break;
}
}
SOPln(gcd);
}
Question: Given two numbers, find their LCM
A = 4 -> 4, 8, 12, 16, 20, 24, 28, ...
B = 5 -> 5, 10, 15, 20, 25, 30, ...
LCM = 20
A = 6 -> 6, 12, 18, 24, 30, 36, 42, ...
B = 7 -> 7, 14, 21, 28, 35, 42, ...
LCM = 42
A = 2 -> 2, 4, 6, 8, 10, 12, 14, ...
B = 9 -> 9, 18, 27, 36, 45, 54, ...
LCM = 18
Show more examples if required.
To build intuition, ask the following questions.
Question 1¶
Minimum number that can be divisible by A and B?
Answer: MAX(A, B)
Explanation:
Let X < MAX(A, B). Then either X < A or X < B. It implies either X is not divisible by A or it is not divisible by B. Hence, it means X is not divisible by at least one of A and B. Thus, any number less than MAX(A, B) cannot be divisible by both.
Maximum number that must be divisible by A and B
Answer: A*B
Explanation: A*_B is divisible by both A and B clearly. Also, it is possible that any number till A _B is not divisible by both A and B. However, as we touch the minimum level of A B, it is divisible by both A and B.
Question 2¶
What is the range of LCM of two numbers A and B?
Expected: MAX(A, B) to A * B
int A = scn.nextInt();
int B = scn.nextInt();
int max = 0;
if (A > B) {
max = A;
}
else{
max = B;
}
int lcm = 0;
for(int i = max; i <= A * B; i ++ ) {
if (i % A == 0 && i % B == 0) {
lcm = i;
break;
}
}
SOPln(lcm);
Question¶
What is the LCM of 6 and 9?
Choices¶
- 18
- 9
- 6
- 1
Relation between GCD and LCM¶
GCD * LCM = A B
Question¶
How many iterations will be there in this loop
for (i = 1; i <= 100; i++) {
S = S + i;
}
Choices¶
- 99
- 100
- 98
- 101
Explanation
The loop will iterate 100 times. Starting from i = 1, the loop will continue as long as i is less than or equal to 100, incrementing i by 1 in each iteration. Therefore, the loop will execute a total of 100 iterations.
Question¶
How many iterations will be there in this loop
for (i = 3; i <= 50; i++) {
S = S + i;
}
Choices¶
- 47
- 48
- 49
- 50
Explanation
The loop will iterate 48 times. Starting from i=3, the loop will continue as long as i is less than or equal to 50, incrementing i by 1 in each iteration. Therefore, the loop will execute a total of 48 iterations as 50 - 3 + 1 = 48.
Question¶
How many iterations will be there in this loop
for (i = 1; i <= N; i++) {
S = S + i;
}
Choices
- N^2
- N
- N / 2
- logN
Explanation:
The number of iterations in this loop depends on the value of N. If N is a positive integer, the loop will iterate N times. Starting from i = 1, the loop will continue as long as i is less than or equal to N, incrementing i by 1 in each iteration.
Question¶
How many iterations will be there in this loop Given N > 0
for (i = 0; i < N; i++) {
S = S + i;
}
Choices¶
- N - 1
- N
- N / 2
- logN
Explanation:
The loop will iterate N times. Starting from i = 0, the loop will continue as long as i is less than N, incrementing i by 1 in each iteration.
Question
How many iterations are made by the code below?
for (i = 1; i <= N; i++) {
print(i);
}
for (j = 1; j <= M; j++) {
print(j);
}
Choices¶
- N
- M
- N * M
- N + M
- 2N
Explanation:
The code consists of two separate loops. The first loop iterates N times, and the second loop iterates M times. Therefore, the total number of iterations made by the code is N + M.
Question¶
How many iterations will the following code make?
for (i = 1; i <= 2^N; i++) {
System.out.println("Hi");
}
Choices¶
- NlogN
- 2^N
- N^2
- N
- Infinite
Explanation:
The code will make 2^N iterations.
Question¶
How many iterations will be there in this loop
for (i = 1; i <= 3; i++) {
for (j = 1; j <= 4; j++) {
print("Hi");
}
}
Choices¶
- 10
- 11
- 12
- 13
Explanation:
The number of iterations in the loop will be 12. This is because the outer loop will run 3 times, and the inner loop will run 4 times each time the outer loop runs. So, the total number of iterations is 3 * 4 = 12.
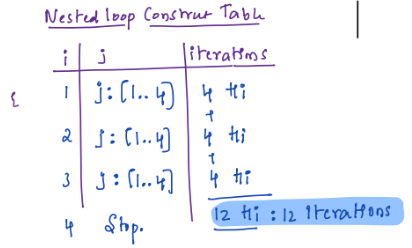
Here is a breakdown of the loop:
- The outer loop runs 3 times, from i = 1 to i = 3.
- Each time the outer loop runs, the inner loop runs 4 times, from j = 1 to j = 4.
- So, the total number of iterations is 3 * 4 = 12.
Question¶
How many iterations will be there in this loop
for (i = 1; i <= 10; i++) {
for (j = 1; j <= N; j++) {
print("Hi");
}
}
Choices¶
- N
- 10N
- 10logN
- 10sqrt(N)
Explanation:
The number of iterations in the loop will be 10*N, where N is the upper bound of the inner loop. This is because the outer loop will run 10 times, and the inner loop will run N times each time the outer loop runs. So, the total number of iterations is 10 N.
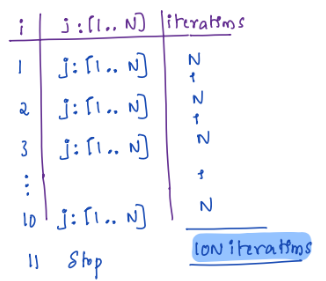
Here is a breakdown of the loop:
- The outer loop runs 10 times, from i = 1 to i = 10.
- Each time the outer loop runs, the inner loop runs N times, from j = 1 to j = N.
- So, the total number of iterations is 10 * N.
Question¶
How many iterations will be there in this loop
for (i = 1; i <= N; i++) {
for (j = 1; j <= N; j++) {
print("Hi");
}
}
Choices
- 2N
- N * N
- logN
- sqrt(N)
Explanation:
The number of iterations in the loop will be N^2, where N is the upper bound of both loops. This is because the outer loop will run N times, and the inner loop will run N times each time the outer loop runs. So, the total number of iterations is \(N\* N=N^2\)
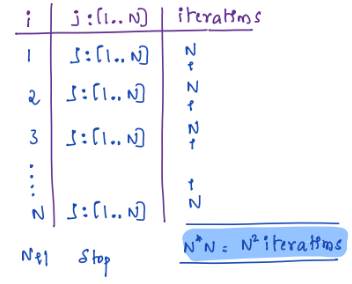
Here is a breakdown of the loop:
The outer loop runs N times, from i = 1 to i = N.
Each time the outer loop runs, the inner loop runs N times, from j = 1 to j = N. So, the total number of iterations is \(N\* N=N^2\)
Question¶
How many iterations will be there in this loop
for (i = 0; i < N; i++) {
for (j = 0; j <= i; j++) {
Print("HI");
}
}
Choices¶
- N * N
- Infinite
- N(N + 1) / 2
- None of them
Explanation:
The number of iterations in the loop will be , \(N(N+1)/2\) where N is the upper bound of the outer loop. This is because the inner loop will run from j = 0 to j = i, and each time the inner loop runs, it prints "HI", so the number of times the inner loop runs is i + 1. So, the total number of iterations is N * (i + 1), which can be simplified to \(N(N+1)/2\)

Here is a breakdown of the loop:
- The outer loop runs N times, from i = 0 to i = N - 1.
- Each time the outer loop runs, the inner loop runs i+1 times, from j = 0 to j = i.
- So, the total number of iterations is N * (i + 1).
Example
How many iterations will this make?
void func(int N){
for(int i = 1; i < n; i++){
for(int j = 1;j <= i; j++){
print("Hi");
}
}
}
The code you provided will print "Hi" a total of \(N(N+1)/2\) times, where N is the number passed to the func() function. For example, if N is 3, then the code will print "Hi" 9 times.
Here is a table of the iterations for N = 3:
| i | j | Iterations |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 2 | 2 |
| 2 | 1 | 3 |
| 2 | 2 | 4 |
Build intuition for continue Statement¶
Print all numbers from 1 to 10 except 5 and 7.
for(int i = 1; i <= 10; i ++ ) {
if (i != 5 && i != 7) {
SOPln(i);
}
}

Observation: In the above code, we are effectively skipping two iterations of the for loop.
For this purpose, we have a statement called the continue statement.
Same example using continue:
for(int i = 1; i <= 10; i ++ ) {
if (i == 5 || i == 7) {
continue;
}
SOPln(i);
}
Question¶
Determine the output of the following code:
for(int i = 0; i <= 5; i ++ ){
if(i == 3){
continue;
}
System.out.println(i + " ");
}
Choices¶
- 0 1 2 3 4 5
- 0 1 2
- 0 1 2 4 5
Explanation:

Question¶
Determine the output of the following code:
public static void main(String args[]) {
for(int i = 1; i <= 10; i ++ ) {
if(i == 4 && i == 6) {
continue;
}
System.out.println(i);
}
}
Choices¶
- Print all numbers except 4 and 6
- Print all numbers
- Error
