Patterns Introduction¶

Agenda¶

Some abbreviations that will be used in this class:

System.out.print - SOP
System.out.println - SOPln

We will work with patterns today. After this class, the students will feel very comfortable with loops.

Print stars in a single row
Print a square
Print a rectangle
Print staircase
Print reverse staircase
Print special pattern

Question¶

Loop to print " * " N times in a single row? Ex: N = 5, print ***** N = 9, print *********

Choices¶

for(int i = 1; i <= N; i++) { SOP(" * "); }
for(int i = 1; i < N; i++) { SOP(" * "); }
for(int i = 0; i <= N; i++) { SOP(" * "); }

Explanation¶

for(int i = 1; i <= N; i++) {
    SOP(" * ");
}

This choice is correct. The code uses a loop to iterate from i = 1 to i = N (both inclusive). In each iteration, it prints the "" character using the SOP("*"); statement. This loop will print "" N times in a single row, as desired.

Certainly, let's take a look at why the other two choices are incorrect:

Incorrect Choice 2:

for (int i = 1; i < N; i++) {
    SOP(" * ");
}

Explanation:

This code uses a loop that starts from i = 1 and continues until i is less than N. In each iteration, it prints an asterisk. However, this loop only iterates N - 1 times, which means it will print one less asterisk than the desired value. For example, if N is 5, this loop will print **** (4 asterisks) instead of *****.

Incorrect Choice 3:

for (int i = 0; i <= N; i++) {
    SOP(" * ");
}

Explanation:

This code uses a loop that starts from i = 0 and continues until i is less than or equal to N. In each iteration, it prints an asterisk. However, this loop iterates N + 1 times, which means it will print one more asterisk than the desired value. For example, if N is 5, this loop will print ****** (6 asterisks) instead of *****.

Example 1¶

This is the quiz question. Print N starts " * " in a single row. N = 5, ***** N = 4, **** N = 2, **

Q. What should be the number of iterations?

A. "N"

Code:

 public static void main() {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        for (int i = 1; i <= n; i++) {
            System.out.print(" * ");
        }
    }

Dry run the codes and justify why Option 1 is correct for some values of N.

Example 2¶

Print a square (N * N) of stars.

For example,

N = 4

****
****
****
****

N = 5

*****
*****
*****
*****
*****

Q. If you have to repeat a single task N number of tasks, how to do that?

A. We can write a loop.

Now, this questions is similar to repeating 1^st task N number of times. So, the code can be:

for (int i = 1; i <= N; i++) {
    for (int i = 1; i <= N; i++) {
        SOP(" * ");
    }
    SOPln();
}

Ask students if this code is correct. It's not, because we cannot repeat variable 'i' in java. So, the final correct code is:

for (int i = 1; i <= N; i++) {
    for (int j = 1; j <= N; j++) {
        SOP(" * ");
    }
    SOPln();
}

Explain why we need SOPln() after the 2^nd for loop.

Explanation:

Without the SOPln() statement after the inner loop, all the asterisks would be printed in a single continuous line, and the pattern would not be formed with rows and columns. The SOPln() call ensures that each row of asterisks is printed on a new line, creating the desired pattern.

Dry run the above code for N = 3.

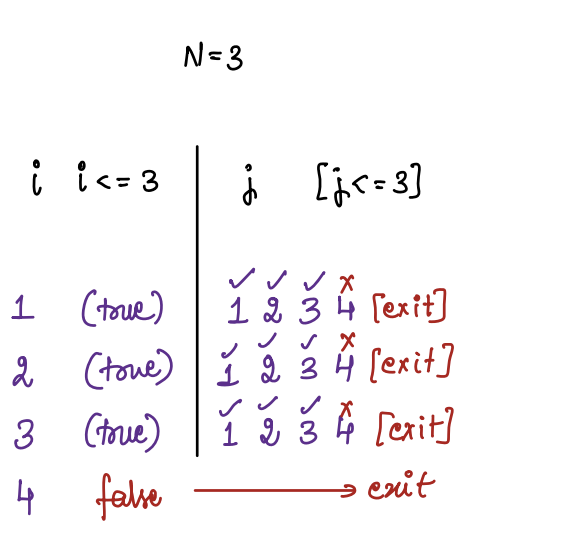
Example 3¶

Print rectangle of N * M having stars. N rows having M stars in each row.

For example,

N = 4, M = 3

***
***
***
***

N = 2, M = 4

****
****

Outer loop -> N times

Inner loop -> M times

The correct code is:

for (int i = 1; i <= N; i++) {
    for (int j = 1; j <= M; j++) {
        SOP(" * ");
    }
    SOPln();
}

Note: Mention that the starting values does not matter. Just that the number of iterations should be N.

Dry run for N = 2, M = 3.

Observation Table:

Row	Stars
1	3
2	3

ith row => M stars

and a total N rows

Example 4¶

Print staircase pattern. For example,

N = 4

*
**
***
****

Warning

Please take some time to think about the solution approach on your own before reading further.....

Observe for each row number i, we have i stars in that row.

Outer Loop -> N times Inner Loop -> i times Inner loop does not work for constant number of times.

Observation Table:

Row	Stars
1	1
2	2
3	3
4	4
5	5

ith row => i stars

The correct code is:

for (int i = 1; i <= N; i++) {

    // Loop to print i stars.
    for (int j = 1; j <= i; j++) {
        SOP(" * ");
    }
    SOPln();
}

Dry run this code for N = 4 (Given image is incomplete).

You may complete the dry run or stop in-between according to the batch.

Example 5¶

Note for instructor: Give some context of why we are learning this approach. Like, as similar approach will work in majority of pattern questions

Print reverse staircase pattern.

For example,

N = 4

****
***
**
*

N = 5

*****
****
***
**
*

For N = 5, we are printing stars in the following manner.

Row + star = N + 1

So, star = N + 1 - Row

Observe for each row number i, we have N - i + 1 stars in that row.

Outer Loop -> N times

Inner Loop -> N - i + 1 times

Inner loop does not work for constant number of times.

The correct code is:

for (int i = 1; i <= N; i++) {

    // Loop to print N - i + 1 stars.
    for (int j = 1; j <= N - i + 1; j++) {
        SOP(" * ");
    }
    SOPln();
}

Dry run the code for N = 3.

Another Approach¶

In this approach, we will change the starting value of i itself.

The correct code is:

for (int i = N; i >= 1; i--) {

    // Loop to print i stars.
    for (int j = 1; j <= i; j++) {
        SOP(" * ");
    }
    SOPln();
}

Example 6¶

Print the diamond pattern.

For example,

N = 5

**********
****--****
***----***
**------**
*--------*
*--------*
**------**
***----***
****--****
**********

You are only supposed to print star " * ", but not underscores (they should be spaces).

If N = 5, so 10 rows are needed.

Warning

Please take some time to think about the solution approach on your own before reading further.....

The pattern can be broken into two halves.

Again, we can break this pattern into halves again.

For the right quarter, we need to print some spaces first and then stars. The table shows for each row, how many spaces and stars need to be printed.

Combining everything for the first half, we have the following table.

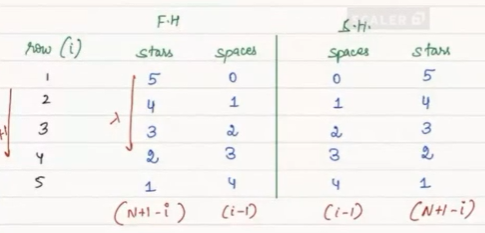
In one single row,

print (N + 1 - i) stars + (i - 1) spaces + (i - 1) spaces + (N + 1 - i) stars

So, print (N + 1 - i) stars + 2 * (i - 1) spaces + (N + 1 - i) stars

So, let's write the code for the upper half using the above facts.

for (int i = 1; i <= N; i++) {

    // In each row, print N + 1 - i stars.
    for (int j = 1; j <= N + 1 - i; j++) {
        SOP(" * ");
    }

    // In each row, (i - 1) spaces.
    for (int j = 1; j <= 2 * (i - 1); j++) {
        SOP(" _ ");
    }

    // In each row, print N + 1 - i stars.
    for (int j = 1; j <= N + 1 - i; j++) {
        SOP(" * ");
    }
    SOPln();
}

Lower Half:

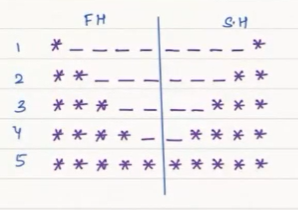
For lower part, we can directly write the following table:

In one single row,

print i stars + print (N - i) spaces + print (N - i) spaces + i stars

So, print i stars + print 2 * (N - i) spaces + i stars

So, let's write the code for the upper half using the above facts.

for (int i = 1; i <= N; i++) {

    // In each row, print N + 1 - i stars.
    for (int j = 1; j <= i; j++) {
        SOP(" * ");
    }

    // In each row, (i - 1) spaces.
    for (int j = 1; j <= 2 * (N - i); j++) {
        SOP(" _ ");
    }

    // In each row, print N + 1 - i stars.
    for (int j = 1; j <= i; j++) {
        SOP(" * ");
    }
    SOPln();
}

Combining these 2 codes we get, the diamond pattern.

Example 7¶

Print the following pattern:

For example,

N = 5

1
2 3 
4 5 6
7 8 9 10
11 12 13 14 15

N = 4

We will create a variable and print that variable. After printing, we increment it.

int val = 1;
for (int i = 1; i <= N; i++) {
    for (int j = 1; j <= i; j++) {
        SOP(val);
        val++;
    }
    SOPln();
}

Explanation:

In the given approach we have initialized a variable val to 1. It employs an outer loop that iterates from 1 to N, governing the rows. Within this loop, an inner loop runs from 1 to the current value of the outer loop index, controlling the values within each row. It prints the value of val, increments it, and then proceeds with the next iteration of the inner loop. This structure creates a pattern where each row holds an increasing sequence of numbers. The SOPln() statement at the end of the outer loop iteration ensures a new line for the subsequent row. By iteratively printing values and managing rows through nested loops, the code systematically generates the desired pattern of numbers.

Example 8¶

Print the following pattern: For example,

N = 5

Warning

Please take some time to think about the solution approach on your own before reading further.....

Approach 1:

for (int i = 1; i <= N; i++) {

    int val = 1;
    for (int j = 1; j <= i; j++) {
        SOP(val);
        val++;
    }
    SOPln();
}

Approach 2:

In this approach instead of taking an extra variable we can directly print j.

for (int i = 1; i <= N; i++) {
    for (int j = 1; j <= i; j++) {
        SOP(j);
    }
    SOPln();
}

Example 9¶

Print the following pattern.

For example,

N = 5

The pattern now starts at each row with that row number. So, only 1 change is required i.e, in the initial value of val.

The correct code for this pattern is:

for (int i = 1; i <= N; i++) {

    int val = i;
    for (int j = 1; j <= i; j++) {
        SOP(val);
        val++;
    }
    SOPln();
}